Cân Bằng Của Điện Tích Là Gì? Kiến Thức Vật Lý 11 Và Cách Giải Bài Tập Chuẩn
Nguyên Lý Và Điều Kiện Cân Bằng Của Điện Tích
Cân bằng của điện tích là một khái niệm quan trọng trong chương trình Vật lý 11, thường xuất hiện trong các bài kiểm tra và đề thi học kỳ. Bài viết này sẽ giúp bạn hiểu rõ bản chất cân bằng lực điện giữa các điện tích điểm, điều kiện để hệ điện tích ở trạng thái cân bằng, và cách vận dụng kiến thức vào giải bài tập chuẩn. Có ví dụ minh họa và hướng dẫn chi tiết từng bước.
A. Công Thức Tính Cân Bằng Của Các Điện TíchĐiện tích cân bằng
* Phương pháp:
Hai điện tích:
Hai điện tích 
\(q_{1};q_{2}\) đặt tại hai điểm A và B, hãy xác định điểm C đặt điện tích \(q_{o}\)để \(q_{o}\) cân bằng:
- Điều kiện cân bằng của điện tích \(q_{o}\):
\({\overrightarrow{F}}_{o} =
{\overrightarrow{F}}_{10} + {\overrightarrow{F}}_{20} =
\overrightarrow{0}\) \(\Leftrightarrow\) \({\overrightarrow{F}}_{10} = -
{\overrightarrow{F}}_{20}\)
\(\Rightarrow\) \(\left\{ \begin{matrix}
{\overrightarrow{F}}_{10} \uparrow \downarrow {\overrightarrow{F}}_{20}
\\
F_{10} = F_{20} \\
\end{matrix} \right.\) \(\begin{matrix}
(1) \\
(2) \\
\end{matrix}\)
+ Trường hợp 1: \(q_{1};q_{2}\) cùng dấu:
Từ (1) \(\Rightarrow\) C thuộc đoạn thẳng AB: AC + BC = AB (*)
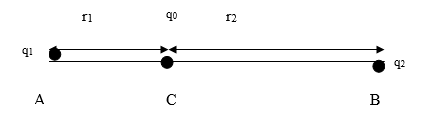
Ta có: \(\frac{\left| q_{1}
\right|}{r_{1}^{2}} = \frac{\left| q_{2}
\right|}{r_{2}^{2}}\)
+ Trường hợp 2: \(q_{1};q_{2}\)trái dấu:
Từ (1) \(\Rightarrow\) C thuộc đường thẳng AB: \(|AC - BC| = AB\)(* ’)
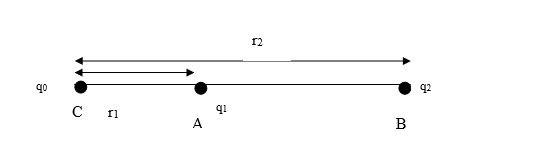
Ta cũng vẫn có: \(\frac{\left| q_{1}
\right|}{r_{1}^{2}} = \frac{\left| q_{2}
\right|}{r_{2}^{2}}\)
- Từ (2) \(\Rightarrow\) \(\left| q_{2} \right|.AC^{2} - \left| q_{1}
\right|.BC^{2} = 0\) (**)
- Giải hệ hai pt (*) và (**) hoặc (* ’) và (**) để tìm AC và BC.
* Nhận xét:
- Biểu thức (**) không chứa \(q_{o}\) nên vị trí của điểm C cần xác định không phụ thuộc vào dấu và độ lớn của \(q_{o}\).
- Vị trí cân bằng nếu hai điện tích trái dấu thì điểm cân bằng nằm ngoài đoạn AB về phía điện tích có độ lớn nhỏ hơn.còn nếu hai điện tích cùng dấu thì nằm giữa đoạn nối hai điện tích.
Ba điện tích:
- Điều kiện cân bằng của q0 khi chịu tác dụng bởi q1, q2, q3:
+ Gọi \({\overrightarrow{F}}_{0}\) là tổng hợp lực do q1, q2, q3 tác dụng lên q0:
\({\overrightarrow{F}}_{0} =
{\overrightarrow{F}}_{10} + {\overrightarrow{F}}_{20} +
{\overrightarrow{F}}_{30} = \overrightarrow{0}\)
+ Do q0 cân bằng: \({\overrightarrow{F}}_{0} =
\overrightarrow{0}\)
\(\Rightarrow \left. \ \begin{matrix}
{\overrightarrow{F}}_{10} + {\overrightarrow{F}}_{20} +
{\overrightarrow{F}}_{30} = \overrightarrow{0} \\
\overrightarrow{F} = {\overrightarrow{F}}_{10} +
{\overrightarrow{F}}_{20} \\
\end{matrix} \right\} \Rightarrow \overrightarrow{F} +
{\overrightarrow{F}}_{30} = \overrightarrow{0} \Leftrightarrow \left\{
\begin{matrix}
\overrightarrow{F} \uparrow \downarrow {\overrightarrow{F}}_{30} \\
F = F_{30} \\
\end{matrix} \right.\)
B. Các Dạng Bài Tập Về Cân Bằng Điện Tích Trong Vật Lý 11
Bài 1. Hai điện tích \(q_{1} = 2.10^{-
8}C;q_{2} = - 8.10^{- 8}C\) đặt tại A và B trong không khí, AB = 8cm. Một điện tích \(q_{o}\)đặt tại C. Hỏi:
a/ C ở đâu để \(q_{o}\) cân bằng?
b/ Dấu và độ lớn của \(q_{o}\) để \(q_{1};q_{2}\) cũng cân bằng?
ĐS: a/ CA = 8cm; CB = 16cm; b/ \(q_{o} = - 8.10^{- 8}C\).
Bài 2. Hai điện tích \(q_{1} = - 2.10^{-
8}C;q_{2} = - 1,8.10^{- 7}C\)đặt tại A và B trong không khí, AB = 8cm. Một điện tích \(q_{3}\)đặt tại C. Hỏi:
a/ C ở đâu để \(q_{3}\) cân bằng?
b*/ Dấu và độ lớn của \(q_{3}\) để \(q_{1};q_{2}\) cũng cân bằng?
ĐS: a/ CA = 4cm; CB = 12cm; b/ \(q_{3} = 4,5.10^{- 8}C\).
Bài 3*. Hai quả cầu nhỏ giống nhau, mỗi quả có điện tích q và khối lượng m = 10g được treo bởi hai sợi dây cùng chiều dài \(l = 30cm\) vào cùng một điểm O. Giữ quả cầu 1 cố định theo phương thẳng đứng, dây treo quả cầu 2 sẽ bị lệch góc\(\alpha = 60^{o}\) so với phương thẳng đứng. Cho \(g = 10m/s^{2}\). Tìm q?
ĐS: \(q = l\sqrt{\frac{mg}{k}} =
10^{- 6}C\)
Bài 4. Hai điện tích điểm q1 = 10-8 C, q2 = 4. 10-8 C đặt tại A và B cách nhau 9 cm trong chân không.
a. Xác định lực tương tác giữa hai điện tích?
b. Xác định vecto lực tác dụng lên điện tích q0 = 3. 10-6 C đặt tại trung điểm AB.
c. Phải đặt điện tích q3 = 2. 10-6 C tại đâu để điện tích q3 nằm cân bằng?
Bài 5. Hai điện tích điểm q1 = q2 = -4. 10-6C, đặt tại A và B cách nhau 10 cm trong không khí. Phải đặt điện tích q3 = 4. 10-8C tại đâu để q3 nằm cân bằng?
Bài 6. Hai điện tích q1 = - 2. 10-8 C, q2= -8. 10-8 C đặt tại A và B trong không khí, AB = 8 cm. Một điện tích q3 đặt tại C. Hỏi: a. C ở đâu để q3 cân bằng? b. Dấu và độ lớn của q3 để q1 và q2 cũng cân bằng ?
Bài 7: Ba quả cầu nhỏ khối lượng bằng nhau và bằng m, được treo vào 3 sợi dây cùng chiều dài l và được buộc vào cùng một điểm. Khi được tách một điện tích q như nhau, chúng đẩy nhau và xếp thành một tam giác đều có cạnh a. Tính điện tích q của mỗi quả cầu?
ĐS: \(\sqrt{\frac{ma^{3}g}{k\sqrt{3(3l^{2}
- a^{2})}}}\)
Bài 8: Cho 3 quả cầu giống hệt nhau, cùng khối lượng m và điện tích.Ở trạng thái cân bằng vị trí ba quả cầu và điểm treo chung O tạo thành tứ diện đều. Xác định điện tích mỗi quả cầu?
ĐS:\(|q| =
l\sqrt{\frac{mg}{\sqrt{6}k}}\)
-----------------------------------
Qua bài viết Cân bằng của điện tích là gì?, bạn đã nắm vững kiến thức nền tảng và cách áp dụng công thức vào giải bài tập Vật lý 11 hiệu quả. Để học tốt phần này, bạn nên luyện tập thêm nhiều dạng đề có đáp án chi tiết và kết hợp ôn lại kiến thức về định luật Coulomb. Hãy tiếp tục khám phá các chủ đề khác trong chương trình Vật lý 11 để tự tin bước vào kỳ thi!
