Công thức Vật lý 12 Con lắc lò xo
Công thức Lý 12 Con lắc lò xo
VnDoc.com xin gửi tới bạn đọc bài viết Công thức Con lắc lò xo để bạn đọc cùng tham khảo. Bài viết dưới đây sẽ cho bạn biết được những công thức tính nhanh bài tập về con lắc lò xo như khảo sát dao động con lắc lò xo về mặt động lực học, về mặt năng lượng, con lắc lò xo nằm ngang, con lắc lò xo nằm nghiêng, con lắc lò xo treo thẳng đứng. Mời các bạn cùng tham khảo bài viết dưới đây.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 12, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 12 sau: Nhóm Tài liệu học tập lớp 12. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Công thức vật lý 12 con lắc lò xo đầy đủ
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
1. Con lắc lò xo
- Con lắc lò xo là hệ thống bao gồm 1 lò xo có độ cứng k (xét tại điều kiện lý tưởng): một đầu cố định, một đầu gắn vật nặng có khối lượng m.
- Phương trình ly độ của con lắc:
![]() \(x = A\cos \left( {\omega t + \varphi } \right)\)
\(x = A\cos \left( {\omega t + \varphi } \right)\)
2. Chu kì và tần số của con lắc lò xo
- Tần số góc của con lắc lò xo: ![]() \(\omega = \frac{k}{m} = \sqrt {\frac{g}{{\Delta {l_0}}}}\)
\(\omega = \frac{k}{m} = \sqrt {\frac{g}{{\Delta {l_0}}}}\)
- Công thức chu kì của con lắc lò xo:  \(T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{k}}\)
\(T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{k}}\)
- Tần số của con lắc lò xo: ![]() \(f = \frac{1}{T} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}\)
\(f = \frac{1}{T} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}\)
Chú ý: Nếu trong thời gian vật thực hiện được N dao động thì tần số là: ![]() \(f = \frac{N}{t}\)
\(f = \frac{N}{t}\)
| Khối lượng vật | ||
| Chu kì | ||
| Tần số |
- Thời gian nén và giãn của lò xo:  \(\left\{ {\begin{array}{*{20}{c}} {{t_{nen}} = \dfrac{{{\varphi _{nen}}}}{\omega }} \\ {{t_{nen}} + {t_{dan}} = T} \end{array}} \right.\). Trong đó:
\(\left\{ {\begin{array}{*{20}{c}} {{t_{nen}} = \dfrac{{{\varphi _{nen}}}}{\omega }} \\ {{t_{nen}} + {t_{dan}} = T} \end{array}} \right.\). Trong đó:  \(\left\{ {\begin{array}{*{20}{c}}
{{\varphi _{nen}} = 2\alpha } \\
{\cos \alpha = \dfrac{{\Delta l}}{{Aa}}}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{\varphi _{nen}} = 2\alpha } \\
{\cos \alpha = \dfrac{{\Delta l}}{{Aa}}}
\end{array}} \right.\)
| Ghép nối tiếp | Ghép song song | |
| Hình vẽ minh họa | 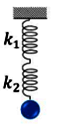 |
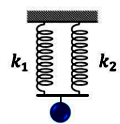 |
| Độ cứng của lò xo | ||
| Chu kỳ |
3. Năng lượng của con lắc lò xo
a. Động năng của con lắc lò xo (J)
![]() \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\left( {\omega t + \varphi } \right)\)
\({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\left( {\omega t + \varphi } \right)\)
- Động năng cực đại: ![]() \({W_{d\max }} = \frac{1}{2}m{v^2}_{\max }\) với vmax là vận tốc cực đại. đv: m/s
\({W_{d\max }} = \frac{1}{2}m{v^2}_{\max }\) với vmax là vận tốc cực đại. đv: m/s
b. Thế năng của con lắc lò xo (J)
![]() \({W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\left( {\omega t + \varphi } \right)\)
\({W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\left( {\omega t + \varphi } \right)\)
- Thế năng cực đại: ![]() \({W_{t\max }} = \frac{1}{2}k{x^2}_{\max } = \frac{1}{2}k{A^2}\)
\({W_{t\max }} = \frac{1}{2}k{x^2}_{\max } = \frac{1}{2}k{A^2}\)
c. Cơ năng của con lắc lò xo (năng lượng toàn phần) (J)
![]() \(W = {W_d} + {W_t} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}\)
\(W = {W_d} + {W_t} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}\)
- Cơ năng của con lắc tỉ lệ với bình phương biên độ dao động, không phụ thuộc vào khối lượng vật nặng.
- Nếu tại t1 ta có x1, v1 và tại t2 ta có x2, v2. Tìm ω, A thì ta có công thức:  \(\left\{ {\begin{array}{*{20}{c}}
{\omega = \sqrt {\dfrac{{{v_2}^2 - {v_1}^2}}{{{x_1}^2 - {x_2}^2}}} } \\
{A = \sqrt {{x_1}^2 + \dfrac{{{v_1}^2}}{{{\omega ^2}}}} }
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{\omega = \sqrt {\dfrac{{{v_2}^2 - {v_1}^2}}{{{x_1}^2 - {x_2}^2}}} } \\
{A = \sqrt {{x_1}^2 + \dfrac{{{v_1}^2}}{{{\omega ^2}}}} }
\end{array}} \right.\)
- Cho biết k; m và W. Tìm vmax và amax:  \(\left\{ {\begin{array}{*{20}{c}}
{{v_{\max }} = \omega .A} \\
{{a_{\max }} = {v_{\max }}.\omega = \dfrac{{{v^2}_{\max }}}{A}}
\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}
{{v_{\max }} = \omega .A} \\
{{a_{\max }} = {v_{\max }}.\omega = \dfrac{{{v^2}_{\max }}}{A}}
\end{array}} \right.\)
- Khi  \({W_d} = n{W_t} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{x = \pm \dfrac{A}{{\sqrt {n + 1} }}} \\
\begin{gathered}
a = \pm \dfrac{{{a_{\max }}}}{{\sqrt {n + 1} }} \hfill \\
v = \pm \dfrac{{{v_{\max }}}}{{\sqrt {\frac{1}{n} + 1} }} \hfill \\
\end{gathered}
\end{array}} \right.\)
\({W_d} = n{W_t} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{x = \pm \dfrac{A}{{\sqrt {n + 1} }}} \\
\begin{gathered}
a = \pm \dfrac{{{a_{\max }}}}{{\sqrt {n + 1} }} \hfill \\
v = \pm \dfrac{{{v_{\max }}}}{{\sqrt {\frac{1}{n} + 1} }} \hfill \\
\end{gathered}
\end{array}} \right.\)
- Khoảng thời gian ngắn nhất giữa hai lần liên tiếp động năng bằng thế năng là: ![]() \(\frac{T}{4}\)
\(\frac{T}{4}\)
- Khoảng thời gian 2 lần liên tiếp động năng hoặc thế năng bằng không là: ![]() \(\frac{T}{2}\)
\(\frac{T}{2}\)
4. Lực đàn hồi của con lắc lò xo thẳng đứng
- Chiều dài lò xo tại VTCB: lcb = l0 + Δl
+ Chiều dài cực tiểu (khi vật ở vị trí cao nhất): lmin = l0 + Δl – A
+ Chiều dài cực đại (khi vật ở vị trí thấp nhất): lmax = l0 + Δl + A
- Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng thì độ lớn lực đàn hồi có biểu thức:
* Fđh = k|Δl + x| với chiều dương hướng xuống
* Fđh = k|Δl – x| với chiều dương hướng lên
a. Nếu Δl >A:
- Lực đàn hồi cực đại : Fmax = k(Δl + A)
- Lực đàn hồi cực tiểu : Fmin = k(Δl – A)
b. Nếu Δl < A:
- Lực đàn hồi cực đại : Fmax = k(A – Δl) ; lúc vật ở vị trí cao nhất
- Lực đàn hồi cực tiểu: Fmin = 0 (lúc vật đi qua vị trí lò xo không biến dạng)
c. Khi ở vị trí cân bằng thì: Fđh = k.Δl = mg
5. Lực đàn hồi của con lắc lò xo nằm ngang
- Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)
- Lực đàn hồi: Fđh = k.x (x: là li độ)
+ Lực đàn hồi cực đại: Fđhmax = k.A (A: biên độ dao động)
+ Lực đàn hồi cực tiểu : Fmin = 0
⇒ VnDoc mời bạn đọc tham khảo tài liệu: Bài tập con lắc lò xo có đáp án
--------------------------------------------------------
Trên đây VnDoc.com vừa giới thiệu tới bạn đọc Công thức tính nhanh bài tập con lắc lò xo. Mong rằng qua đây các bạn có thể học tập tốt hơn môn Vật lý lớp 12. Mời các bạn cùng tham khảo thêm kiến thức các môn Toán 12, Tiếng Anh 12, Ngữ văn 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...



