Đề khảo sát chất lượng đầu năm lớp 12 môn Toán năm 2015 - 2016 trường THPT Hàn Thuyên, Bắc Ninh

Đề khảo sát chất lượng đầu năm lớp 12 môn Toán

Đề khảo sát chất lượng đầu năm lớp 12 môn Toán năm 2015 - 2016 trường THPT Hàn Thuyên, Bắc Ninh được VnDoc.com sưu tầm và đăng tải là đề kiểm tra đầu năm lớp 12, giúp các bạn học sinh mới từ lớp 11 lên lớp 12 ôn tập và hệ thống lại kiến thức của mình một cách hiệu quả, chuẩn bị tốt cho năm học mới. Mời các bạn tham khảo.

Đề khảo sát chất lượng đầu năm môn Tiếng Anh lớp 12 trường THPT Thuận Thành 1, Bắc Ninh năm 2015 - 2016

Đề thi khảo sát chất lượng đầu năm lớp 12 năm 2012 - 2013 tỉnh Gia Lai

Câu 1 (2,0 điểm). Cho hàm số y = f(x) = x³ - 3x² - 9x - 1, có đồ thị (C).

a) Tìm tọa độ các điểm trên đồ thị (C), có hoành độ x₀ thỏa mãn f'(x₀) = 0.

b) Viết phương trình tiếp tuyến với đồ thị (C), tại giao điểm của đồ thị (C) và trục Oy.

Câu 2 (1,0 điểm). Giải phương trình √3 cosx + sinx - 2cos2x = 0.

Câu 3 (1,0 điểm).

a) Tính giới hạn

b) Tìm số hạng không chứa x trong khai triển

Câu 4 (1,0 điểm).

a) Cho cos2α = 1/5. Tính giá trị của biểu thức P = 1 - tan²α.

b) Một chiếc hộp đựng 6 quả cầu trắng, 4 quả cầu đỏ và 2 quả cầu đen. Chọn ngẫu nhiên 4 quả. Tính xác suất để 4 quả được chọn có đủ cả 3 màu.

Câu 5 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho A(1; 5) và đường thẳng Δ: x + 2y - 1 = 0. Tìm tọa độ điểm A' đối xứng với điểm A qua đường thẳng Δ và viết phương trình đường tròn đường kính AA'.

Câu 6 (1,0 điểm). Cho hình chóp đều S.ABCD, có đáy ABCD là hình vuông cạnh a. Góc giữa cạnh bên và mặt đáy bằng 60⁰. Tính diện tích tam giác SAC và khoảng cách giữa hai đường thẳng SA và CD.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD. Điểm E(7; 3) là một điểm nằm trên cạnh BC. Đường tròn ngoại tiếp tam giác ABE cắt đường chéo BD tại điểm N (N ≠ B). Đường thẳng AN có phương trình 7x + 11y + 3 = 0. Tìm tọa độ các đỉnh A, B, C, D của hình vuông ABCD, biết A có tung độ dương, C có tọa độ nguyên và nằm trên đường thẳng 2x - y - 23 = 0.

Câu 8 (1,0 điểm). Giải hệ phương trình

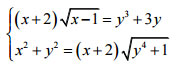
Câu 9 (1,0 điểm). Cho ba số thực x, y, z ∈ [1; 2]. Tìm giá trị lớn nhất của biểu thức:

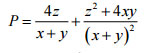
Đáp án đề khảo sát chất lượng đầu năm lớp 12 môn Toán

Câu 1 (2,0 điểm).

a) Ta có f'(x) = 3x² - 6x - 9

f'(x) = 0 ↔ 3x² - 6x - 9 = 0 ↔ x = -1 hoặc x = 3

Với x = -1 → y = 4 → M₁(-1;4)

Với x = 3 → y = -28 → M₂(3; -28)

b) Giáo của (C) và Oy là A(0; -1). Ta có: f'(0) = -9

Phương trình tiếp tuyến: y = -9x - 1

Câu 2 (1,0 điểm).

√3 cosx + sinx - 2cos2x = 0 ↔ √3/2 cosx + 1/2 sinx = cos2x

↔ cos2x = cos(x - π/6) ↔ 2x = x - π/6 + k2π hoặc 2x = -x + π/6 + k2π

Thu gọn ta được nghiệm: x = -π/6 + k2π; x = π/18 + k2π/3

Câu 3 (1,0 điểm)

a) Ta có:

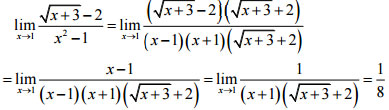
b) Số hạng tổng quát là:

Ta phải có: 24 - 3k = 0 ↔ k =8 → Số hạng không chứa x: C⁸₁₂2⁸ = 126720.