Đề khảo sát Toán (chuyên) vào 10 năm 2024 - 2025 trường chuyên Lam Sơn, Thanh Hóa
Đề thi tuyển sinh lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
ZIP
Phân loại:
Tài liệu Tính phí
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐỀ THI CHÍNH THỨC
( Đề thi có 01 trang)
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
THPT CHUYÊN LAM SƠN
Năm học: 2024 – 2025
Môn thi: TOÁN
(Dành cho thí sinh thi vào chuyên Toán)
Ngày thi: 07/4/2024
Thời gian làm bài:150 phút (không kể thời gian phát đề)
Câu 1. a) Cho
,xy
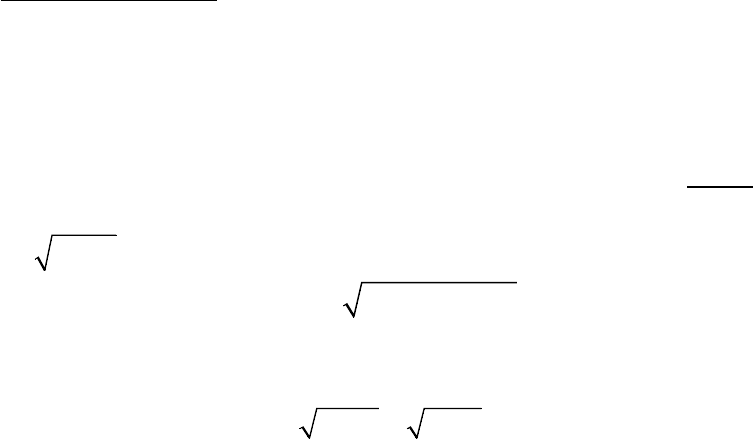
là các số hữu tỉ dương thỏa mãn
2
22
1
2,
xy
xy
xy
+
++ =
+
chứng
minh
1 xy+
là số hữu tỉ.
b) Cho biểu thức
8
( ) 12 12 3Px x x x= − ++
. Gọi
0
x
là một nghiệm của
phương trình
2
10xx
+ −=
. Tính giá trị
0
( ).Px
.
Câu 2. a) Giải phương trình:
2
3 - 2 5 -1 3.x x xx+ = −+
b) Giải hệ phương trình
3
2
(3 2 ) 8
( 3 3) 4.
xy
xy y y
+=
+ +=
Câu 3. a) Giải phương trình nghiệm nguyên dương:
22
5( ) 7( 2 ).x xy y x y++ = +
b) Cho
n
là số nguyên dương và
d
là ước dương của
2
2,n
chứng minh
2
nd
+
không phải là số chính phương.
Câu 4. Tam giác nhọn không cân
ABC
nội tiếp đường tròn
( ),O
đường cao
( ).AH H BC∈
Gọi
,KL
lần lượt là hình chiếu vuông góc của điểm
H
trên các
cạnh
,.AB AC
Đường thẳng
KL
cắt đường tròn
()O
tại hai điểm
,PQ
(
P
và
B
cùng phía đối với
AC
).
a) Chứng minh tứ giác
BKLC
nội tiếp đường tròn.
b) Chứng minh
BC
là tiếp tuyến của đường tròn ngoại tiếp tam giác
.PHQ
c)
AH
cắt lại đường tròn
()O
tại
( ).TT A≠
Gọi
D
là hình chiếu vuông
góc của
H
lên
;KL AD
cắt đường tròn
()O
tại
( ).MM A≠
Chứng minh
0
90 .HMT =
Câu 5. Chứng minh rằng từ
6
số vô tỉ tùy ý ta có thể chọn được
3
số
,,abc
sao
cho cả
3
số
,,abbcca+++
đều là số vô tỉ. Bài toán còn đúng không nếu ban đầu
là
4
số?
………………………….. Hết …………………………
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:................................................................... Số báo danh:..........................
Chữ kí của giám thị số 1 : ……………………………………..….Chữ kí của giám thị số 2:………………
1
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐỀ THI CHÍNH THỨC
( Đề thi có 01trang)
KỲ THI KHẢO SÁT CÁC MÔN THI VÀO LỚP 10
THPT CHUYÊN LAM SƠN
Năm học: 2024 - 2025
Môn thi: Toán (chuyên Toán)
Ngày thi:
Thời gian làm bài:150 phút (không kể thời gian phát đề)
ĐÁP ÁN (Chuyên Toán)
Câu 1. a) Ta có:
2
22
1
2
xy
xy
xy
+
++ =
+
⇔
( ) ( )
2
2
1
21 0
xy
x y xy
xy
+
+ − ++ =
+
(0,25đ)
⇔
2
1 11
00
xy xy xy
xy xy xy
xy xy xy
+ ++
+− =⇔+− =⇔+=
+ ++
(0,25đ)
( )
2
11xy x y xy x y⇔ += + ⇔ + = +
(0,5đ)
b) Ta có
2 2 42
00 0 0 00 0 0 0 0
10 1 21(1)2123
xx x x xx x x x x+ −=⇒ =− ⇒ = − += − − += −
.
82
00 0
9 12 4xx x⇒= − +
(0,5đ)
Do đó
2
0 0 0 0 00
( ) 9 24 16 3 4 3 3 ,Px x x x x x= − ++ =− +
(0,25đ)
mà
2
000
4 3 3(1 ) 1 3 1 0.xxx− = − += +>
Vậy
0 00
( ) 4 3 3 4.Px x x=−+=
(0,5đ)
Câu 2. a) ĐK:
2/3x ≥
. Ta có:
( )
( )
22
22
2
3x-2 5x-1 3 3x-2 1 5x-1 ( 3 2) 0
3x+2 ( 1) (5x-1)
( 3 2) 0 (0,5 )
3x-2 5x-1 ( 1)
xx x x x x
xx
xx d
xx
+ = − + ⇔ − + +− + − + =
− +−
⇔ + + −+=
+ ++
2
11
( 3 2) 1 0
3x-2 5x-1 ( 1)
xx
xx
⇔ − + + +=
+ ++
Ta có:
11
1 0, 2 / 3
3x 1 ( 1) 5x 4 ( 2)
x
xx
+ +> ∀≥
+++ +++
Suy ra:
2
3 2 0 1, 2 ( )x x x x tm− +=⇔= =
KL:
1, 2.xx= =
(0,5đ)
2
b) Từ hệ suy ra
0.x ≠
Hê
(
)
( )
33
3
32
88
32 12 1
44
33 1 1
yy
xx
yyy y
xx
+ = + +=
⇔⇔
+ += +=+
Đặt
2
1
u
x
vy
=
= +
ta được hệ phương trình:
( )
( )
3
3
2 1 1
2 1 2
uv
vu
= +
= +
(0,5đ)
( )
( )
33 2 2
2( ) 2 0u v v u u v u uv v⇒−= −⇔− +++=
Vì
22
2u uv v+++
> 0, nên
uv=
Từ (1) suy ra :
3
2 10uu− −=
1
15
2
uv
uv
= = −
⇒
±
= =
Với
12
uv xy
= =−⇒ = =−
Với
51
15
51
2
2
x
uv
y
= −
+
= = ⇒
−
=
Với
51
15
51
2
2
x
uv
y
=−−
−
= = ⇒
−−
=
(0,5đ)
Câu 3. a) Từ giả thiết suy ra:
( ) ( )
7 25 25 2 5 5 2xy xy xymxmy+⇒+⇒+=⇒=−
( )
*
m∈
Thay vào phương trình ta có:
( ) ( )
2
2
52 52 70
my myyy m− + − +− =
22
3 15 25 7 0 (0,25 )y my m m d⇔ − + −=
Phương trình (ẩn y)có nghiệm nên
( )
22 2
84
225 12 25 7 0 75 84 0 0
75
m mm m m m
∆= − − ≥ ⇒ − ≤ ⇔ ≤ ≤
(0,25đ)
Do m là số nguyên nên
0m
=
(loại), hoặc
1m
=
Với
1m =
, ta được
( )( )
( ) ( )
2
52
52
, 1, 2
2 30
3 15 18 0
xy
xy
xy
yy
yy
= −
= −
⇒=
− −=
− +=
(0,5đ)
Nhận xét. Cũng có thể giải câu 3a) theo cách sau:
Giải phương trình nghiệm nguyên dương:
22
5( ) 7( 2 ).x xy y x y++ = +
Vì
,*xy∈
, ta có:
22 2 2
5( ) 7( 2 ) 5(4 4 4 ) 28( 2 )x xy y x y x xy y x y++ = + ⇔ + + = +
( ) (
)
2
2
15 5 2 28 2x xy xy⇔ ++ = +
( ) ( )
2
28
52 282 2
5
xy xy xy⇒ + < + ⇒+ <
Đề thi khảo sát Toán (chuyên) vào 10 năm 2024 - 2025 trường chuyên Lam Sơn, Thanh Hóa
VnDoc.com xin gửi tới các bạn Đề thi thử vào lớp 10 môn Toán trường Chuyên Lam Sơn, Thanh Hóa năm 2024 - 2025 để bạn đọc cùng tham khảo. Đây là tài liệu hay cho các bạn ôn luyện, chuẩn bị cho kì thi tuyển sinh vào lớp 10 sắp tới. Đề thi có đáp án đi kèm cho các bạn so sánh đối chiếu sau khi làm xong. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây.


