Đề thi Olympic lớp 7 môn Toán trường Xuân Dương năm 2014 - 2015

Đề thi Olympic lớp 7 môn Toán

Đề thi Olympic môn Toán lớp 7 trường THCS Xuân Dương, Thanh Oai năm 2014 - 2015 gồm 5 câu hỏi tự luận, làm trong thời gian 120 phút giúp các bạn học sinh lớp 7 luyện tập và nâng cao kỹ năng môn Toán, từ đó đạt điểm số cao trong các bài thi, bài kiểm tra. Mời các bạn tham khảo.

Đề thi Olympic Vật lý lớp 7 trường THCS Bích Hòa, Hà Nội năm 2014 - 2015

Bài 1: (6đ)

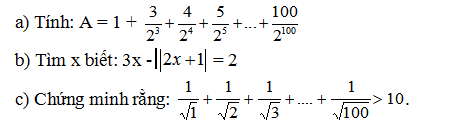
Bài 2: (4đ)

a) Tính giá trị của đa thức sau:

A = x^₂ + x⁴ + x⁶ + x⁸ + ...+ x¹⁰⁰ tại x = -1.

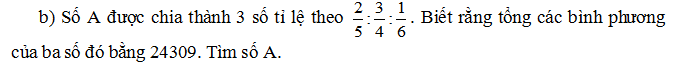
Bài 3: (4đ)

a) Tìm số nguyên x sao cho: (x² -1)( x_² -4)( x² -7)(x² -10) < 0.

Đáp án đề thi Olympic lớp 7 môn Toán trường Xuân Dương

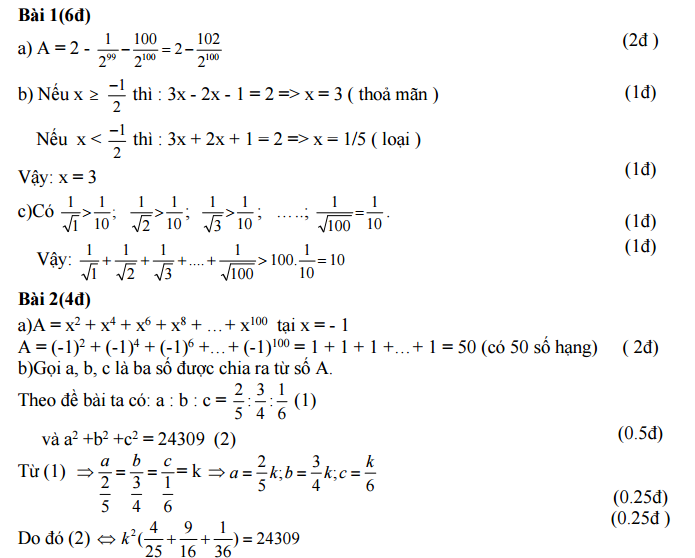
Bài 3: (4đ)

a) Vì tích của 4 số: x^₂ – 1 ; x² – 4; x² – 7; x² – 10 là số âm nên phải có 1 số âm hoặc 3 số âm.

Ta có: x² – 10< x² – 7< x² – 4< x² – 1. (1đ)

Xét 2 trường hợp:

Có1 số âm : x² – 10 < x² – 7→ x² – 10 < 0 < x² – 7

7< x² < 10→ x² =9 ( do x Z ) x = ± 3. (0,5đ)

Có 3 số âm, 1 số dương.

x2 – 4< 0< x2 – 1→ 1 < x2 < 4

do x Z nên không tồn tại x (0,5đ)

Vậy x =± 3 (0,5đ)

Bài 5: (1đ)

25 - y² = 8(x - 2009)² (0.25đ)

Ta có 8(x-2009)² = 25- y²

8(x-2009)²+y2=25 (*) (0.25đ)

Vì y² ≥ 0 nên (x-2009)² ≤ 25/8, suy ra (x-2009)² = 0 hoặc (x-2009)² =1

Với (x -2009)² =1 thay vào (*) ta có y² = 17 (loại)

Với (x- 2009)² = 0 thay vào (*) (0.25đ)

ta có y2 =25 suy ra y = 5 (do y € N)

Từ đó tìm được (x=2009; y=5) (0.25đ)