Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 3)
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 3) là đề thi thử đại học môn Toán có đáp án đi kèm, dành cho các bạn và thầy cô tham khảo ôn luyện môn Toán chuẩn bị cho kì thi đại học năm 2016 sắp tới.
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 1)
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội (Lần 2)
| TRƯỜNG THPT CHUYÊN NGUYỄN HUỆ |
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN THỨ BA NĂM HỌC: 2015 - 2016 ĐỀ THI MÔN:TOÁN Thời gian làm bài: 180 phút |
Câu 1 (2 điểm): Cho hàm số y = x4 + 2mx2 - 2m + m4 (với m là tham số )
- Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1.
- Tìm m để hàm số có cực đaị, cực tiểu và các điểm cực đại, cực tiểu của đồ thi ̣hàm số tạo thành một tam giác có một góc bằng 1200.
Câu 2 (1 điểm): Giải phương trình: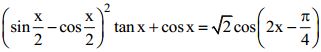 
.
Câu 3 (1 điểm): Tính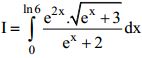 
.
Câu 4 (1 điểm):
- Tìm tập hợp những điểm M trên mặt phẳng phức biểu diễn số phức 2z + i - 3 thỏa mãn:
- Giải bất phương trình:
Câu 5 (1 điểm): Trong không gian Oxyz cho đường thẳng 
, mặt phẳng (P): 2x + y - z - 4 = 0 và điểm A(2; 1; -1). Viết phương trình mặt phẳng (Q) chứa d và vuông góc với (P). Tìm hai điểm B, C lần lượt trên đường thẳng d và mặt phẳng (P) sao cho A là trung điểm của BC?
Câu 6 (1 điểm): Cho hình chóp S.ABC. Đáy là tam giác ABC có AB = a, BC = 2BA, góc ABC = 60o. Cạnh bên SB của hình chóp tạo với đáy góc 60o. Hình chiếu của đỉnh S trên mặt phẳng đáy trùng với trọng tâm G của tam giác ABC. Tính thể tích hình chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC).
Câu 7 (1 điểm):Trong măṭ phẳng tọa độ Oxy cho hình thoi ABCD có hai đường chéo AC = 2BD và ngoại tiếp đường tròn (C): (x - 3)2 + (y - 4)2 = 10. Đường thẳng AB đi qua điểm M(-2; -1). Tìm tọa độ điểm A biết hoành độ xA của nó là môṭ số âm?
Câu 8 (1 điểm): Giải hệ: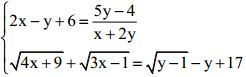 
Câu 9 (1 điểm): Tìm các số thực x, y thỏa mãn: (x + y)2 + 3(x2 + 2x + y) = 0 sao cho biểu thức P = 8x3 + y3 + 3(4x2 + y2) đạt giá tri ̣bé nhất.
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
