Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Định Quán, Đồng Nai (Lần 1)
Đề thi thử THPT Quốc gia môn Toán năm 2016
Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Định Quán, Đồng Nai (Lần 1) là đề thi thử nhằm đánh giá chất lượng học tập cũng như chất lượng ôn thi đại học, ôn thi THPT Quốc gia năm 2016 môn Toán. Đề thi môn Toán có đáp án đi kèm, hi vọng sẽ giúp các bạn củng cố kiến thức hiệu quả nhất. Mời các bạn tham khảo.
Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2
Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Quang, Hải Dương (Lần 1)
|
Trường THPT Định Quán
|
THI THỬ THPT QUỐC GIA NĂM HỌC 2015 – 2016 LẦN 1 MÔN THI: TOÁN Thời gian làm bài: 180 phút, không kể thời gian phát đề |
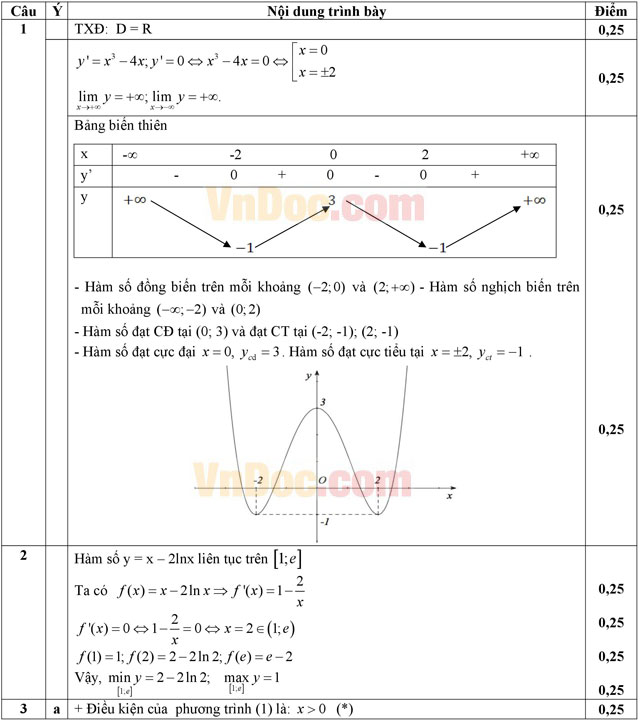
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 
.
Câu 2 (1,0 điểm). Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x - 2lnx trên [1; e].
Câu 3 (1,0 điểm).
a. Giải phương trình 
. (x ∈ R)
b. Tìm môđun của số phức 
biết (2 + i3)z + 1 + 3i = z + i4.
Câu 4 (1,0 điểm). Tính tích phân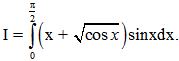 
Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 1) và mặt phẳng (P): x + 2y + 2x - 4 = 0. Viết phương trình mặt cầu (S) tâm I và tiếp xúc với (P). Tìm tọa độ hình chiếu H của I trên (P).
Câu 6 (1,0 điểm).
a. Cho 
. Tính giá trị biểu thức 
.
b. Một hộp chứa 6 bi màu vàng, 5 bi màu đỏ và 4 bi màu xanh có kích thước và trọng lượng như nhau, lấy ngẫu nhiên 8 bi trong hộp. Tính xác xuất sao cho trong 8 bi lấy ra có số bi màu vàng bằng với số bi màu đỏ.
Câu 7 (1,0 điểm). Trong không gian cho hình chóp S.ABC có đáy là tam giác vuông tại B, BC = 3a, AC = a√10, cạnh bên SA vuông góc với đáy, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60o. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SM và AC theo a, biết M là điểm trên đoạn BC sao cho MC = 2MB.
Câu 8 (1,0 điểm). Trong mặt phẳng tọa độ 0xy cho tam giác ABC, có M(3; -1) là trung điểm cạnh BC. Đường thẳng chứa đường cao đỉnh B đi qua E(-1; -3). Đường thẳng chứa cạnh AC đi qua F(1; 3). Tìm tọa độ các đỉnh của tam giác ABC, biết đường tròn ngoại tiếp tam giác ABC có đường kính AD với D(4; -2).
Câu 9 (1,0 điểm). Giải hệ phương trình: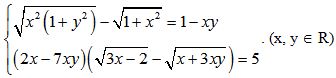 
Câu 10 (1,0 điểm). Cho a, b, c > 0 thỏa mãn a + b + c = 3. Tìm giá trị nhỏ nhất của biểu thức:
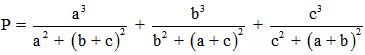
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016
