Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lương Thế Vinh, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lương Thế Vinh, Hà Nội (Lần 1) gồm 9 câu hỏi có đáp án đi kèm, là tài liệu ôn tập môn Toán kì thi THPT Quốc gia hữu ích dành cho các bạn học sinh lớp 12, chuẩn bị bước vào kì thi THPT Quốc gia, xét tuyển vào Đại học, Cao đẳng 2016 khối A, khối B, khối D hiệu quả.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Lương Thế Vinh, Hà Nội (Lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Hóa học trường THPT Lương Thế Vinh, Hà Nội (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Lương Thế Vinh, Đồng Nai (Lần 1)

TRƯỜNG THPT LƯƠNG THẾ VINH HÀ NỘI Năm học 2015 - 2016

ĐỀ THI THỬ THPT QUỐC GIA NĂM 2016 Môn thi: Toán - Lần thứ 1 Thời gian làm bài: 180 phút, không kể thời gian phát đề -------------- Ngày 31.1.2016 --------------

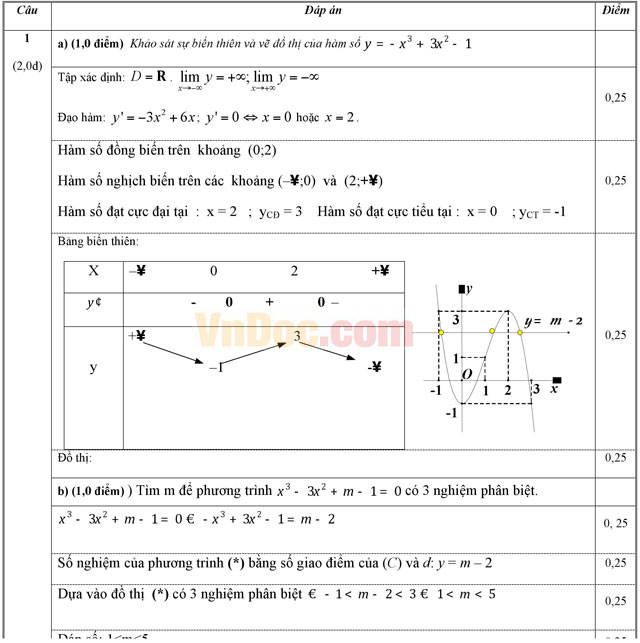
Câu 1 ( 2,0 điểm). Cho hàm số y = -x³ + 3x² - 1 (C)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Tìm m để phương trình x³ - 3x² + m - 1 = 0 có 3 nghiệm phân biệt.

Câu 2 (1,0 điểm).

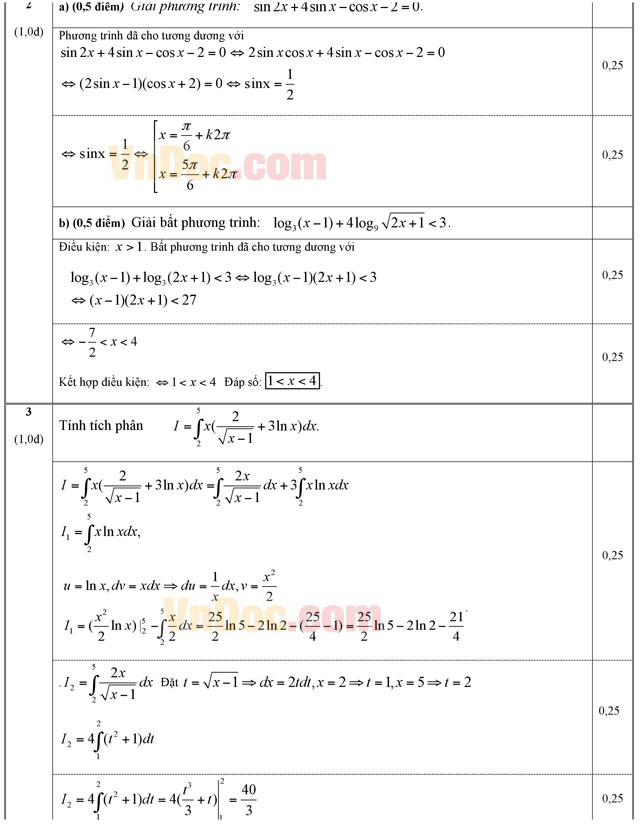
a) Giải phương trình: sin2x + 4sinx - cos2x = 0.

b) Giải bất phương trình: .

Câu 3 (1,0 điểm). Tính tích phân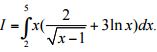

Câu 4 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; -3), B(-2; 1; -4) và mặt phẳng (P): x - 4y + z - 8 = 0. Chứng minh đường thẳng AB song song với mặt phẳng (P). Tìm tọa độ hình chiếu vuông góc của A trên (P).

Câu 5 (1,0 điểm).

a) Tìm hệ số của x³ trong khai triển biểu thức A = (x + 3)⁴ + 5x(2x - 1)⁷.

b) Đội thanh niên tình nguyện trường Lương Thế Vinh gồm 5 học sinh lớp 10, 6 học sinh lớp 11 và 4 học sinh lớp 12. Cần chọn ngẫu nhiên 5 học sinh tham gia công tác tình nguyện tại một tỉnh vùng cao. Tính xác suất để trong 5 học sinh được chọn có ít nhất 2 học sinh lớp 10.

Câu 6 (1,0 điểm). Cho hình chóp S.ABCD, ABCD là hình thang vuông tại A và B; tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD); AB = BC = a, AD = 2a, SA = 2a. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa AD và SB.

Câu 7 (1,0 điểm). Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình đường phân giác trong góc A là x + y - 2 = 0, phương trình trung tuyến kẻ từ A là 4x + 5y - 9 = 0, bán kính đường tròn ngoại tiếp tam giác ABC bằng 15/6. Biết điểm K(3/2; 0) nằm trên đường thẳng AC và điểm C có hoành độ dương. Tìm tọa độ các điểm A, B, C.

Câu 8 (1,0 điểm). Giải phương trình

Câu 9 (1,0 điểm). Cho ba số thực dương x, y, z thỏa mãn: x + y + z = 3.

Tìm giá trị lớn nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016