Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 2) là đề thi thử đại học môn Toán có chất lượng được VnDoc.com sưu tầm và đăng tải. Đề thi môn Toán có đáp án đi kèm sẽ giúp các bạn chủ động khi làm đề thi thử, ôn thi THPT Quốc gia môn Toán hiệu quả. Mời các bạn cùng tham khảo.

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 1)

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành số 3, Bắc Ninh (Lần 1)

SỞ GD & ĐT BẮC NINH TRƯỜNG THPT THUẬN THÀNH SỐ 1

ĐỀ THI THỬ THPT QUỐC GIA LẦN 2 NĂM HỌC: 2015 – 2016 MÔN: TOÁN Thời gian làm bài: 180 phút

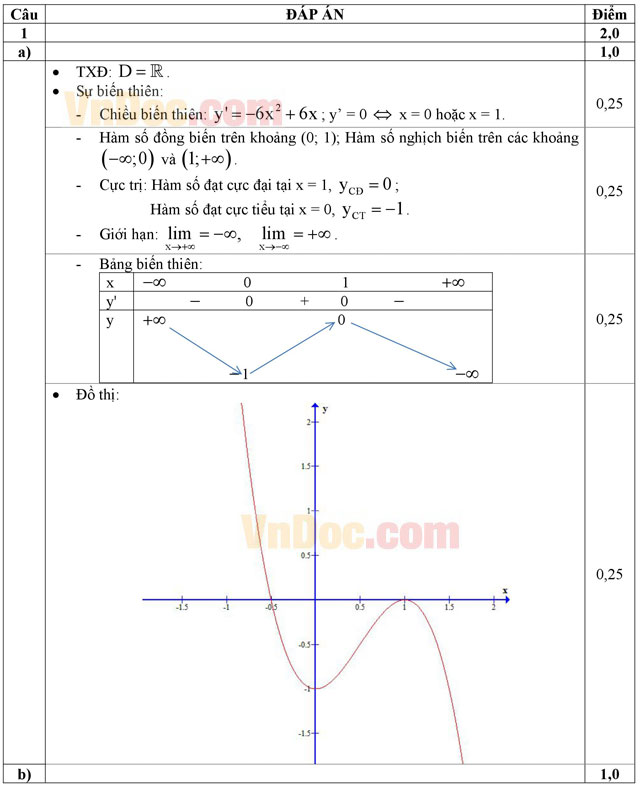
Câu 1 (2,0 điểm). Cho hàm số -2x³ + 3x² - 1

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của (C) với đường thẳng y = -1.

Câu 2 (1,0 điểm)

a) Giải bất phương trình .

b) Tìm số phức z thỏa mãn .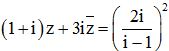

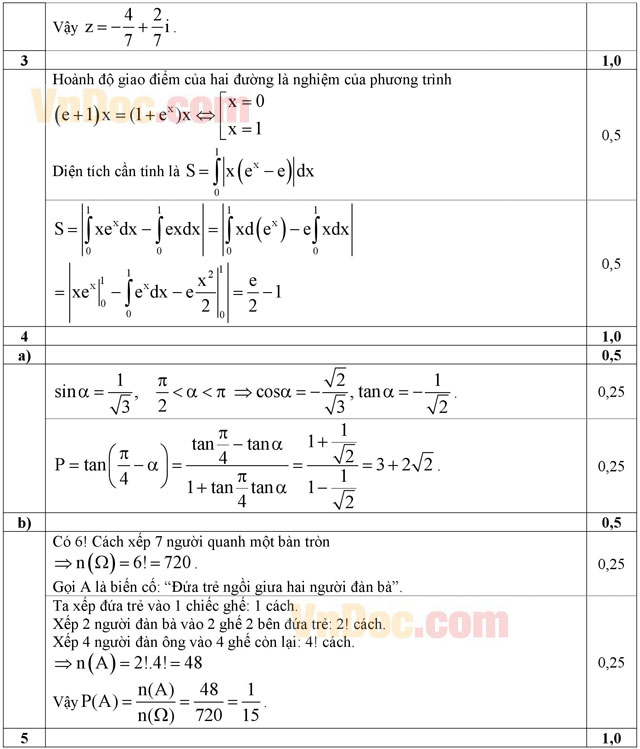
Câu 3 (1,0 điểm). Tính diện tích hình phẳng giới hạn bởi các đường y = (e + 1)x, y = (e^x + 1)x.

Câu 4 (1,0 điểm)

a) Cho sinα = 1/√3, π/2 < α < π. Tính giá trị của biểu thức P = tan(π/4 - α).

b) Xếp ngẫu nhiên bốn người đàn ông, hai người đàn bà và một đứa trẻ ngồi vào bảy chiếc ghế đặt quanh một bàn tròn. Tính xác suất để đứa trẻ ngồi giữa hai người đàn bà.

Câu 5 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của AB. SC tạo với đáy một góc 450. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB, AC.

Câu 6 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – y + 2z = 0 và hai đường thẳng , . Viết phương trình đường thẳng nằm trong mặt phẳng (P), vuông góc với đường thẳng d và cắt đường thẳng d'.

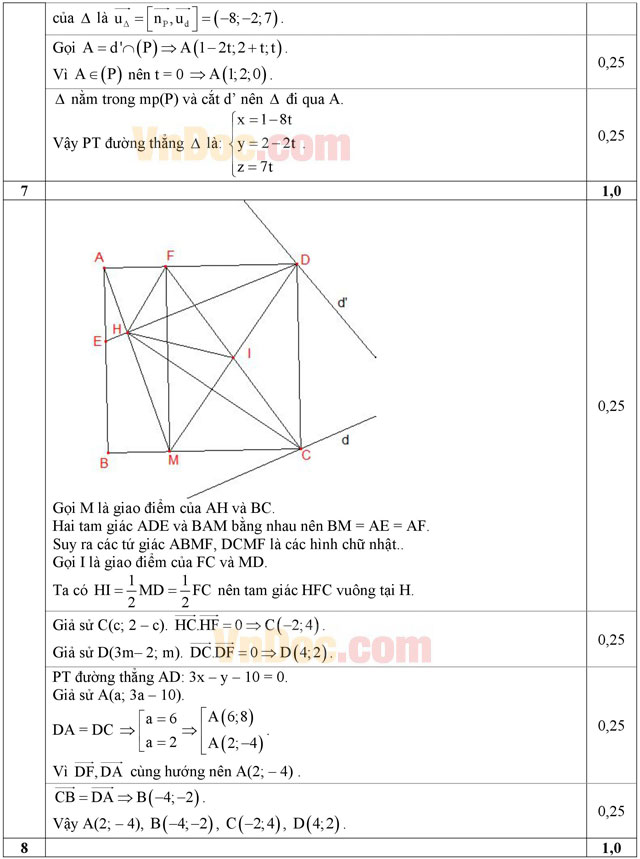
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho hình vuông ABCD. Trên các cạnh AB, AD lần lượt lấy hai điểm E, F sao cho AE = AF. Gọi H là hình chiếu vuông góc của A trên DE. Biết H(2/5; -14/5), F(8/3; -2), C thuộc đường thẳng d: x + y – 2 = 0, D thuộc đường thẳng d': x – 3y + 2 = 0. Tìm tọa độ các đỉnh của hình vuông.

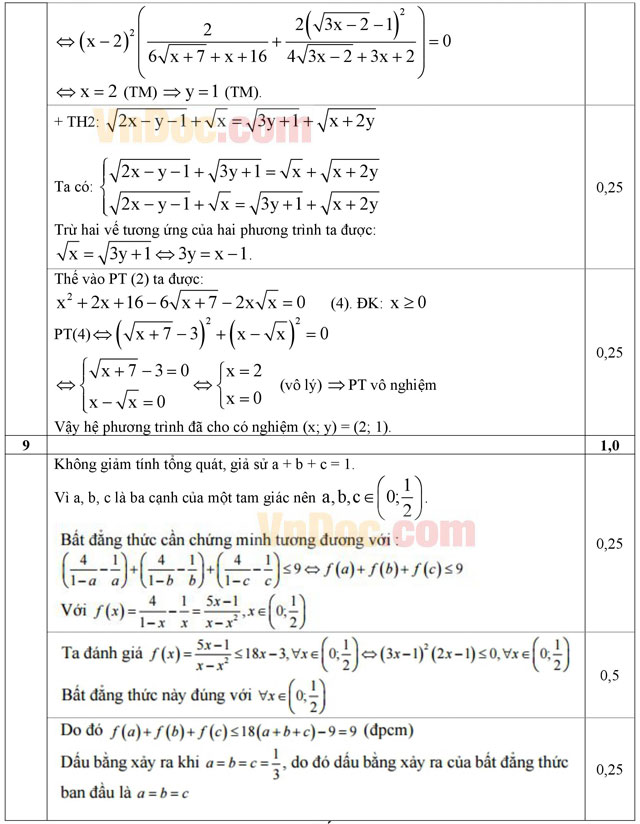
Câu 8 (1,0 điểm). Giải hệ phương trình: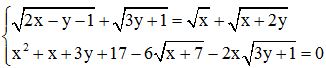

Câu 9 (1,0 điểm). Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh rằng:

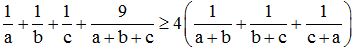
Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016