Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Lĩnh, Hà Tĩnh

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Hồng Lĩnh, Hà Tĩnh là đề thi thử môn Toán đáp án đi kèm được VnDoc.com sưu tầm và đăng tải. Đây là tài liệu tham khảo hữu ích dành cho các bạn thí sinh luyện thi đại học, ôn thi THPT Quốc gia 2016. Chúc các bạn đạt kết quả cao trong kì thi sắp tới.

Đề thi thử THPT Quốc gia năm 2016 môn Toán tỉnh Vĩnh Phúc (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Thanh Chương 1, Nghệ An (Lần 1)

TRƯỜNG THPT HỒNG LĨNH

KỲ THI THỬ THPT QUỐC GIA 2016 Môn thi: TOÁN Thời gian làm bài: 180’ không kể thời gian phát đề

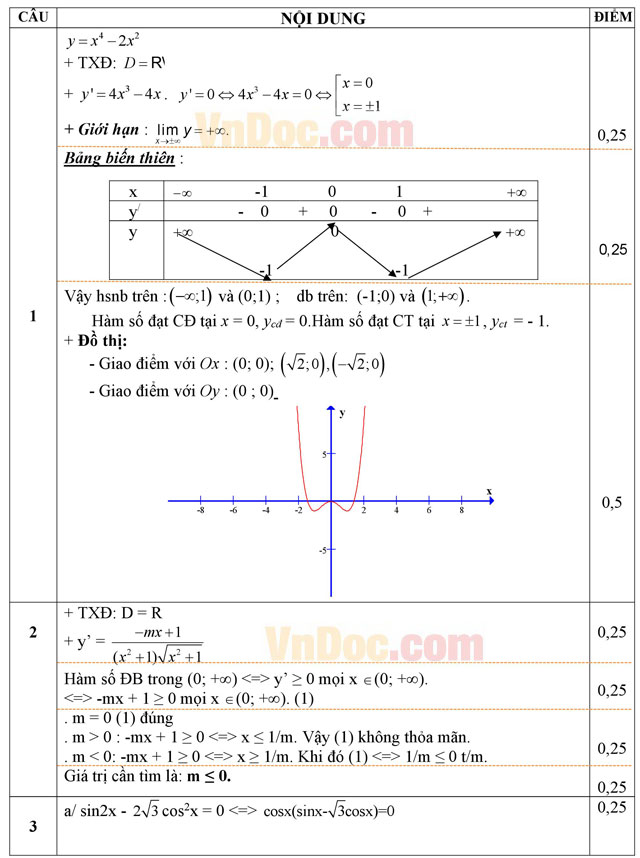
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x⁴ – 2x².

Câu 2 (1,0 điểm). Xác định m để hàm số sau đồng biến trong khoảng (0; +∞):

Câu 3 (1,0 điểm). Giải các phương trình, bất phương trình sau trên tập số thực:

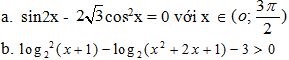
Câu 4 (1,0 điểm). Tính tích phân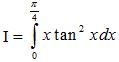

Câu 5 (1,0 điểm). Gọi A là tập hợp tất cả các số tự nhiên gồm các chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5. Lấy ngẫu nhiên một số trong A, tính xác suất để lấy được số có chứa chữ số 3.

Câu 6 (1,0 điểm).

Trong không gian Oxyz cho điểm A(3; -2; -2) và mặt phẳng (P): x - y - z + 1 = 0.

a) Viết phương trình mặt cầu (S) có tâm A và tiếp xúc với mp (P).

b) Viết phương trình mặt phẳng (Q) đi qua A, vuông góc với mp (P) biết rằng mp (Q) cắt hai trục Oy, Oz lần lượt tại điểm phân biệt M và N sao cho OM = ON.

Câu 7 (1,0 điểm). Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc 30⁰. Biết hình chiếu vuông góc của A' trên (ABC) trùng với trung điểm cạnh BC. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và bán kính mặt cầu ngoại tiếp tứ diện A'ABC.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy, cho hình vuông ABCD. Điểm E(2; 3) thuộc đoạn thẳng BD, các điểm H(-2; 3) và K(2; 4) lần lượt là hình chiếu vuông góc của điểm trên và . Xác định toạ độ các đỉnh A, B, C, D của hình vuông ABCD.

Câu 9 (1,0 điểm). Giải bất phương trình sau trên tập R:

Câu 10 (1,0 điểm). Cho a, b, c là ba số thuộc đoạn [0; 1]. Chứng minh:

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán