Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Yên Lạc, Vĩnh Phúc (Lần 1)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Nhằm giúp các bạn học sinh lớp 12, các bạn thí sinh tự do có thêm tài liệu tự ôn thi THPT Quốc gia cũng như ôn thi đại học, VnDoc.com xin giới thiệu Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Yên Lạc, Vĩnh Phúc (Lần 1). Đề thi môn Toán có đáp án, hi vọng sẽ giúp các bạn đạt điểm cao trong kì thi quan trọng sắp tới.

Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Yên Lạc, Vĩnh Phúc

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Yên Lạc 2, Vĩnh Phúc

Câu I (2 điểm). Cho hàm số y = x³ - 3(m + 1)x² + 9x - m, với m là tham số thực.

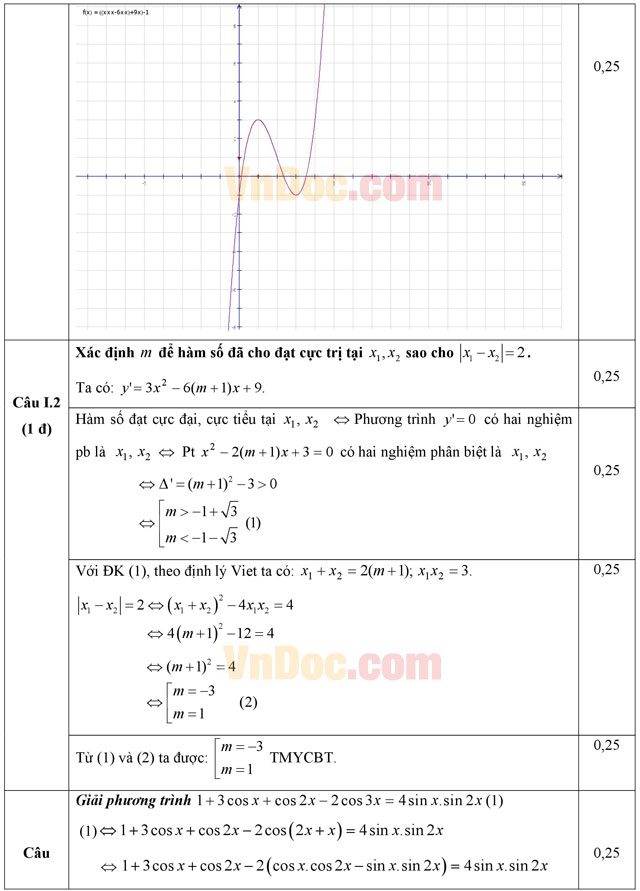
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho với m = 1.

2. Xác định m để hàm số đã cho đạt cực trị tại x₁, x₂ sao cho |x₁ - x₂| = 2.

Câu II (3 điểm). Giải các phương trình, hệ phương trình sau

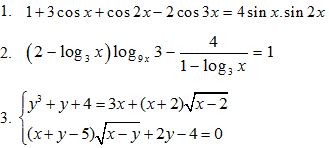
Câu III (1 điểm). Tính tổng .

Câu IV (1 điểm). Cho lăng trụ tam giác ABC.A₁B₁C₁ có tất cả các cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30⁰. Hình chiếu H của điểm A trên mặt phẳng (A₁B₁C₁) thuộc đường thẳng B₁C₁. Tính thể tích khối lăng trụ ABC.A₁B₁C₁ và tính khoảng cách giữa hai đường thẳng AA₁ và B₁C₁ theo a.

Câu V (1 điểm). Tính giới hạn .

Câu VI (1 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C₁): x² + y² = 13 và đường tròn (C₂): (x - 6)² + y² = 25 cắt nhau tại A(2; 3). Viết phương trình đường thẳng đi qua A và lần lượt cắt (C₁), (C₂) theo hai dây cung phân biệt có độ dài bằng nhau.

Câu VII (1 điểm). Cho các số thực dương a, b, c thỏa mãn điều kiện a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức: .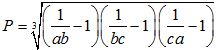

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán