Đề thi thử vào lớp 10 môn Toán năm học 2015-2016 huyện Vũ Thư, Thái Bình
Đề thi thử vào lớp 10 môn Toán
Đề thi thử vào lớp 10 môn Toán năm học 2015-2016 huyện Vũ Thư, Thái Bình là đề thi thử vào lớp 10 môn Toán năm 2015. Đề có đáp án, thuận tiện cho các bạn tra cứu, ôn tập, chuẩn bị tốt cho kì thi tuyển sinh lớp 10 THPT sắp tới. Mời các bạn cùng tham khảo.
Đề thi thử vào lớp 10 môn Toán năm 2015 trường THCS Nguyễn Tất Thành, Hưng Yên
Đề thi thử vào lớp 10 môn Toán năm 2015 trường THPT Chuyên Hà Nội - Amsterdam
|
UBND HUYỆN VŨ THƯ
|
ĐỀ THI THỬ TUYỂN SINH THPT Năm học 2015 - 2016 MÔN THI: TOÁN (Thời gian làm bài: 120 phút) |
Bài 1 (2 điểm)
| 1. Tính | |
2. Cho biểu thức
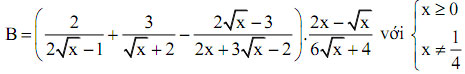
a, Rút gọn biểu thức B.
b, Tìm x sao cho B nhận giá trị nguyên.
Bài 2 (2 điểm)
| 1. Cho hệ phương trình | { | (m + 1)x + my = 2m - 1 |
| mx - y = m2 - 2 |
a, Giải hệ phương trình với m = 4.
b, Chứng minh rằng với mọi m hệ luôn có nghiệm duy nhất (x; y). Tìm m sao cho P = xy + x + 2y đạt giá trị lớn nhất.
2. Giải phương trình: x4 + (2√2 - 1)x2 + 4√2 - 6 = 0.
Bài 3 (2 điểm)
Cho hàm số y = x2 (P) và y = 2(m - 3)x + m - 9 (d), m là tham số, m ϵ Z.
1, Tìm m sao cho (d) là hàm số bậc nhất đồng biến.
2, Tìm m sao cho đồ thị (P) và (d) tiếp xúc nhau, tìm tiếp điểm.
3, Tìm m sao cho đồ thị (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ âm.
Bài 4 (3,5 điểm)
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn, từ A kẻ các tiếp tuyến AB, AC đến đường tròn (B, C là các tiếp điểm). M là điểm bất kì trên cung nhỏ BC, (M khác B và C), gọi D, E, F là hình chiếu vuông góc của M lên BC, CA, AB. Giao điểm của MB với DF là P, của MC với DE là Q. Chứng minh rằng:
1, Các tứ giác MDBF và MDCE nội tiếp.
2, PQ // BC.
3, PQ là tiếp tuyến của đường tròn ngoại tiếp tam giác MQE.
4, Đường thẳng nối giao điểm của đường tròn ngoại tiếp tam giác MQE với đường tròn ngoại tiếp tam giác MPF đi qua 1 điểm cố định.
Bài 5 (0,5 điểm):
Cho các số thực dương a, b, c thỏa mãn a2 + b2 + c2 = 3.
Chứng minh rằng:
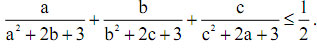
Đáp án đề thi thử vào lớp 10 môn Toán
Bài 1 (2 điểm)
1. Tính được A = 2√5 - 2 (0,5 điểm)
2. a, Rút gọn va kết luận: Vậy với x ≥ 0, x ≠ 1/4 thì b = x/(x + 2) (1,0đ)
b, Tìm được 0 ≤ B < 1. (0,25đ)
B = 0 ↔ √x = 0 ↔ x = 0 (tm) (0,25đ)
Vậy với x = 0 thì B nhận giá trị nguyên.
Bài 2 (2 điểm)
1. a. Thay m, giải hệ và kết luận hệ có nghiệm duy nhất x = 3, y = -2. (0,75đ)
| b. { | (m + 1)x + my = 2m - 1 | ↔ ... ↔ | { | (m2 + m + 1)x = m3 - 1 (1) |
| mx - y = m2 - 2 | y = mx - m2 + 2 |
Do m2 + m + 1 = (m + 1/2)2 + 3/4 ≠ 0 ∀m.
P = 2 ↔ m = 1.
Vậy m = 1 thì P đạt giá trị lớn nhất là 2.
2. Giải được đến tập nghiệm S = {√2 - 1 ; 1 - √2)





