Định nghĩa và các phép toán số phức

VnDoc xin giới thiệu tới các bạn học sinh lớp 12 tài liệu Định nghĩa và các phép toán số phức, hy vọng qua bộ tài liệu các bạn học sinh sẽ có kết quả cao hơn trong học tập. Mời thầy cô và các bạn học sinh cùng tham khảo chi tiết tại đây nhé.

I. Lý thuyết

1. Khái niệm số phức:

Là biểu thức có dạng a + bi, trong đó a, b là những số thực và số i thoả i² = –1.

Kí hiệu là z = a + bi với a là phần thực, b là phần ảo, i là đơn vị ảo.

Tập hợp các số phức kí hiệu là = {a + bi/ a, b ∈ R và i²= –1}. Ta có R ⊂ C.

Số phức có phần ảo bằng 0 là một số thực: z = a + 0.i = a ∈ R ⊂ C

Số phức có phần thực bằng 0 là một số ảo: z = 0.a + bi = bi. Đặc biệt i = 0 + 1.

Số 0 = 0 + 0.i vừa là số thực vừa là số ảo.

2. Số phức bằng nhau:

Cho hai số phức z = a + bi và z’ = a’ + b’i. Ta có z = z¢ ↔ a=a′; b=b′

VD: Tìm các số thực x, y biết: (2x – 3) – (3y + 1) = (2y + 1) + (3x – 7)i (1)

\((1)\Leftrightarrow \left\{\begin{matrix} 2x- 3 = 2y+1 \\ -3y-1=3x-7 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x-y=2 \\ x+y=2 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x=2 \\ y=0 \end{matrix}\right.\)

3. Biểu diễn hình học của số phức:

Mỗi số phức z = a + bi được xác định bởi cặp số thực (a; b).

Trên mặt phẳng Oxy, mỗi điểm M(a; b) được biểu diễn bởi một số phức và ngược lại.

Mặt phẳng Oxy biểu diễn số phức được gọi là mặt phẳng phức. Gốc tọa độ O biểu diễn số 0, trục hoành Ox biểu diễn số thực, trục tung Oy biểu diễn số ảo.

VD: Các điểm A, B, C, D biểu diễn các số phức là:

z_A=1+4i; z_B=−3+0i; z_C=0−2i; z_D=4−i.

4. Môđun của số phức:

Số phức z = a + bi được biểu diễn bởi điểm M(a; b) trên mặt phẳng Oxy. Độ dài của véctơ OM^→ được gọi là môđun của số phức z. Kí hiệu |z|=|a+bi|=\(\sqrt{a^2+b^2}\)

VD: z = 3 – 4i có |z|=|3−4i|=\(\sqrt{3^2+\left(-4\right)^2=5}\)

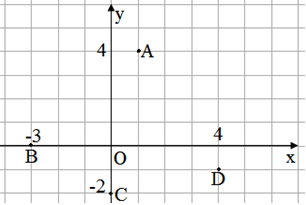
Chú ý: ∣z²∣=∣a²−b²+²abi∣=\(\sqrt{(a^2-b^2)^2+4a^2b^2}=a^2+b^2=|z|^2\)

5. Số phức liên hợp:

Cho số phức z = a + bi, số phức liên hợp của z là z¯=a−bi.

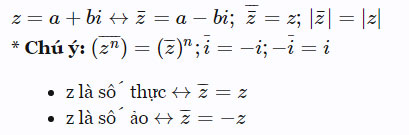
* Môđun số phức z = a + b.i (a; b ∈ R) |z|=|OM|=\(\sqrt{z.z^-}\)

Chú ý: |z|=|z¯|;∀z∈C

Hai điểm biểu diễn z và z¯ đối xứng nhau qua trục Ox trên mặt phẳng Oxy.

6. Cộng, trừ số phức:

Số đối của số phức z = a + bi là –z = –a – bi

Cho z = a + b.i và z’ = a’ + b’i. Ta có z + z’ = (a ± a’) + (b ± b’)

Phép cộng số phức có các tính chất như phép cộng số thực.

7. Phép nhân số phức:

Cho hai số phức z = a + bi và z’ = a’ + b’.i.

Nhân hai số phức như nhân hai đa thức rồi thay i² = –1 và rút gọn, ta được:

k.z = k(a + bi) = ka + kb.i . Đặc biệt 0.z = 0 ∀z∈C

z¯ = (a + bi)(a – bi) hay z.z¯=a²+b²=|z|²

VD: Phân tích z²+ 4 thành nhân tử. z² + 4 = z² – (2i)² = (z – 2i)(z + 2i).

Phép nhân số phức có các tính chất như phép nhân số thực.

8. Phép chia số phức:

Số nghịch đảo của số phức z = a + bi ≠ 0 là z⁻¹=1/z=z¯/|z|² hay 1/a+bi=a−bi/a²+b²

Cho hai số phức z = a + bi ≠ 0 và z’ = a’ + b’i thì z′/z=z′.z¯/|z|² hay a′+b′i/a+bi=(a′+b′i)(a−bi)/a²+b²

VD: Tìm z thoả (1 + 2i)z = 3z – i.

Ta có (3 – 1 – 2i)z = i ↔ z = i/2−2i ↔ z=i(2+2i)/4+4⇔z=−2+2i/8⇔z=−1/4+1/4/i

9. Lũy thừa của đơn vị ảo: Cho k ∈ N

i^4k=1;i^4k+1=i;i^4k+2=−1;i^4k+3=−i

VD: Tìm phần thực và ảo của số phức: z = (2−2i)¹³

z=[(2−2i)²]⁶(2−2i)=(8i)⁶(2−2i)=−8⁶.2+8⁶.2i=−2¹⁹+2¹⁹i

Phần thực a = −2¹⁹, phần ảo b = 2¹⁹

II. Bài tập rèn luyện

1) Tìm các số thực x, y biết:\

a) (3x –2) + (2y +1)i = (x + 1) – (y – 5)i;

b) (1 – 2x) – i3–√ = 5–√ + (1 – 3y)i;

c) (2x + y) + (2y – x)i = (x – 2y + 3) + (y + 2x +1)i;

ĐS:

\(a)\ x=1,5;\ y=\frac{4}{3}\)

\(b)\ x=0;\ y=1\)

\(c)\ x=1-\ \frac{5}{\sqrt{2}};\ y\ =\ 1+\sqrt{3}\)

2) Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn bởi số phức z thỏa:

a) Phần thực của z bằng –2;

b) Phần ảo của z bằng 3;

c) Phần thực của z thuộc khoảng (–1; 2);

d) Phần ảo của z thuộc đoạn [1; 3];

e) Phần thực và phần ảo của z đều thuộc đoạn [–2; 2].

Hướng dẫn​

a) Là đường thẳng x = –2;

b) Là đường thẳng y = 3;

c) Là miền trong giới hạn bởi hai đường thẳng song song x = –1 và x = 2 không tính biên;

d) Là miền trong giới hạn bởi hai đường thẳng song song y = 1 và y = 3 tính cả biên;

e) Là miền trong giới hạn bởi bốn đường thẳng đôi một song song x = –2, x = 2 và y = –2, y = 2 tính cả biên.

3) Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn bởi số phức z thỏa:

a) |z| = 1;

b) |z| ≤ 1

c) 1 < |z| ≤ 2

d) |z| = 1 và phần ảo của z bằng 1.

Hướng dẫn​

a) Tập hợp các điểm M(a; b) thỏa a²+b²=1, là đường tròn tâm O, bán kính R = 1;

b) Tập hợp các điểm M(a; b) thỏa a²+b²≤1, là hình tròn tâm O, bán kính R = 1 tính cả biên;

c) Tập hợp các điểm M(a; b) thỏa 1<a²+b²≤2, là hình vành khăn tâm O, bán kính r = 1 không tính biên, bán kính lớn R = 2 tính biên;

4) Thực hiện các phép tính sau:

a) 2i(3 + i)(2 + 4i)

b) (1+i)2(2i)3/−2+i

5) Giải phương trình sau:

a) (3 – 2i)z + (4 + 5i) = 7 + 3i;

b) (1 + 3i)z – (2 + 5i) = (2 + i)z

c) z/4−3i+(2−3i)=5−2i

Hướng dẫn​

a) z = 1

b) z = 8/5−9/5i

c) z = 15 – 5i.

6)
Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ O trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.

Hướng dẫn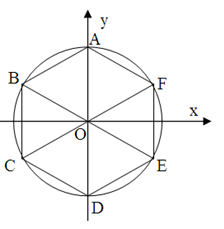Gọi A là điểm biểu diễn số phức i thì D biểu diễn số –i. F(cosπ/6;sinπ/6) nên F biểu diễn số \(\frac{\sqrt{3}}{2}\)+1/2i. C đối xứng F qua O nên C biểu diễn số \(\frac{\sqrt{3}}{2}\)−1/2i. E đối xứng F qua Ox nên E biểu diễn số \(-\frac{\sqrt{3}}{2}\)−1/2i. B đối xứng E qua O nên B biểu diễn số \(-\frac{\sqrt{3}}{2}\)+1/2i

7)

Cho z=−1/2+\(\sqrt{3}\)/2i. Hãy tính: 1/z;z¯;z²;(z¯)³;1+z+z².

Hướng dẫn​

Ta có |z|=1 nên

1z=−1/2−\(\sqrt{3}\)/2i=z¯;

z²=−1/2−\(\sqrt{3}\)/2i;

z^¯3=z¯.z¯²=1;

1+z+z²=0

8) Chứng minh rằng:

a) Phần thực của số phức z bằng 1/2(z+z¯), phần ảo của số phức z bằng 1/2i(z−z¯)

b) Số phức z là số ảo khi và chỉ khi z=−z¯.

c) Số phức z là số thực khi và chỉ khi z=z¯.

Hướng dẫn​

z=a+bi,z¯=a−bi (1)

a) Lấy vế cộng vế → Phần thực của số phức z bằng 1/2(z+z¯). Lấy vế trừ vế → phần ảo của số phức z bằng 1/2i(z−z¯).

b) Số phức z là số ảo khi và chỉ khi phần thực bằng 0 ↔ z+z¯=0⇔z=−z¯.

c) Số phức z là số thực khi và chỉ khi phần ảo bằng 0 ↔ z−z¯=0⇔z=z¯.

d) z=a+bi;z′=a′+b′i;zz¯=a²+b² là số thực

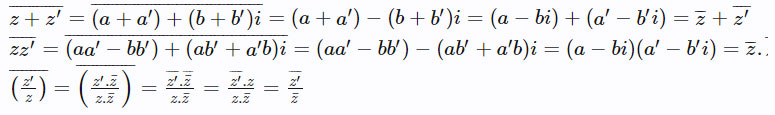
9)

Chứng minh rằng với mọi số nguyên m > 0, ta có i^4m=1;i^4m+1=i;i^4m+2=−1;i^4m+3=−i

Hướng dẫn​

Ta có i⁴=i².i²=1

(i⁴)^m=1^m↔i^4m=1↔i^4m.i=1.i

↔i^4m+1=i↔i^4m+1.i=i.i

↔i^4m+2=−1↔i^4m+2.i=−1.i

↔i^4m+3=−i

10)

Chứng minh rằng:

a) Nếu \(\overrightarrow u\) của mặt phẳng phức biểu diễn số phức z thì \(|\overrightarrow u |\, = \,|z|\) và từ đó nếu hai điểm \({A_1},\,{A_2}\) theo thứ tự biểu diễn số phức \({z_1},\,{z_2}\) thì \(\left| {\overrightarrow {{A_1}{A_2}} } \right| = \left| {{z_2} - {z_1}} \right|.\)

b) Với mọi số phức z, z¢, ta có |z.z'| = |z|.|z'| và khi z ≠ 0 thì \(\left| {\frac{{z'}}{z}} \right| = \frac{{\left| {z'} \right|}}{{\left| z \right|}}\)

c) Với mọi số phức z, z', ta có \(\left| {z + z'} \right| \le \left| z \right| + \left| {z'} \right|\)

a) z = a + bi thì \(\left| z \right| = \sqrt {{a^2} + {b^2}} , \overrightarrow u\) biểu diễn số phức z thì \(\overrightarrow u = (a; b)→ \left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2}}\) do đó \(|\overrightarrow u |\, = \,|z|\)

\({A_1},\,{A_2}\) theo thứ tự biểu diễn số phức

\({z_1},\,{z_2},\ thì \,\overrightarrow {{A_1}{A_2}} = \overrightarrow {O{A_2}} - \overrightarrow {O{A_1}} = {z_2} - {z_1} \Rightarrow \left| {\overrightarrow {{A_1}{A_2}} } \right| = \left| {{z_2} - {z_1}} \right|\)

\(b) z = a + bi, z’ = a’ + b’i, z.z’ = (aa’ - bb’) + (ab’ + a’b)i,\)

\(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| {z'} \right| = \sqrt {a{'^2} + b{'^2}}\)

Ta có \({\left| z \right|^2}.{\left| {z'} \right|^2} = \left( {{a^2} + {b^2}} \right)\left( {a{'^2} + b{'^2}} \right)\)

Ta có

\({\left| {z.z'} \right|^2} = {\left( {aa' - bb'} \right)^2} + {\left( {ab' + a'b} \right)^2} = {\left( {aa'} \right)^2} + {\left( {bb'} \right)^2} + {\left( {ab'} \right)^2} + {\left( {a'b} \right)^2} = \left( {{a^2} + {b^2}} \right)\left( {a{'^2} + b{'^2}} \right)\)

Vậy |z.z'| = |z|.|z'|

Khi z ≠ 0 ta có:

\(\left| {\frac{{z'}}{z}} \right| = \left| {\frac{{z'.\bar z}}{{z.\bar z}}} \right| = \frac{{\left| {z'} \right|.\left| {\bar z} \right|}}{{{{\left| z \right|}^2}}} = \frac{{\left| {z'} \right|.\left| z \right|}}{{{{\left| z \right|}^2}}} = \frac{{\left| {z'} \right|}}{{\left| z \right|}}\)

c) \(\overrightarrow u\) biểu diễn z, \(\overrightarrow u’\) biểu diễn z¢ thì \(\overrightarrow u + \overrightarrow {u'}\) biểu diễn z + z¢ và \(\left| {z + z'} \right| = \left| {\overrightarrow u + \overrightarrow {u'} } \right|\)

Khi \(\overrightarrow u ,\overrightarrow {u'} \ne \overrightarrow 0\), ta có

\({\left| {\overrightarrow u + \overrightarrow {u'} } \right|^2} = {\overrightarrow u ^2} + {\overrightarrow {u'} ^2} + 2\left| {\overrightarrow u } \right|\left| {\overrightarrow {u'} } \right|\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right) \le {\left| {\overrightarrow u } \right|^2} + {\left| {\overrightarrow {u'} } \right|^2} + 2\left| {\overrightarrow u } \right|\left| {\overrightarrow {u'} } \right| = {\left( {\left| {\overrightarrow u } \right| + \left| {\overrightarrow {u'} } \right|} \right)^2}\)

\(→ \left| {\overrightarrow u + \overrightarrow {u'} } \right| \le \left| {\overrightarrow u } \right| + \left| {\overrightarrow {u'} } \right| do \,đó \left| {z + z'} \right| \le \left| z \right| + \left| {z'} \right|\)

12) Tìm số phức thỏa mãn đk ở bài 11 mà có mô đun nhỏ nhất.

13)
Chứng minh rằng với mọi số phức z ¹ 1, ta có \(1+z+z^2+...+z^9=\frac{z^{10}-1}{z-1}\)

\(Với \,z ¹ 1,\)

\(\left( {1 + z + {z^2} + ... + {z^9}} \right)\left( {z - 1} \right) = z + {z^2} + ... + {z^9} + {z^{10}} - \left( {1 + z + {z^2} + ... + {z^9}} \right) = {z^{10}} – 1\)

Chia hai vế cho z – 1 hằng đẳng thức được chứng minh.(Cấp số nhân)

14)

Hỏi mỗi số sau đây là số thực hay số ảo (z là số phức tùy ý sao cho biểu thức xác định)?

\(a) {z^2} + {(\bar z)^2}\)

\(b) \frac{{z - \bar z}}{{{z^3} + {{(\bar z)}^3}}}\)

\(c) \frac{{{z^2} - {{(\bar z)}^2}}}{{1 + z\bar z}}\)

Hướng dẫn​

\(Ta \,có \,z = a + bi,\,\,\bar z = a - bi, \,{z^2} = ({a^2} - {b^2}) + 2abi,\,{\bar z^2} = ({a^2} - {b^2}) - 2abi,\,\)

\(Và \,{z^3} = ({a^3} - 3a{b^2}) + (3{a^2}b - {b^3})i,\,\,{\bar z^3} = ({a^3} - 3a{b^2}) - (3{a^2}b - {b^3})i\)

\(Vậy \,{z^2} + {(\bar z)^2} = 2({a^2} - {b^2})\, là \,số \,thực; \frac{{z - \bar z}}{{{z^3} + {{(\bar z)}^3}}} = \frac{b}{{{a^3} - 3a{b^2}}}i \,là \,số \,ảo;\)
\(\frac{{{z^2} - {{(\bar z)}^2}}}{{1 + z.\bar z}} = \frac{{4ab}}{{1 + {a^2} + {b^2}}}i\, là\, số \,ảo.\)

15)

Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thỏa điều kiện sau:

a) \(z^2\) là số thực âm;

b) \(z^2\) là số ảo;

\(c) {z^2} = {(\bar z)^2}\)

\(d)\ \frac{1}{z-i}\ là\ số\ ảo\)

M(x; y) biểu diễn z thì \(z = x + yi \Rightarrow {z^2} = {x^2} - {y^2} + 2xyi;\,\,{\bar z^2} = {x^2} - {y^2} - 2xyi\)

a) \({z^2}\) là số thực âm khi xy = 0 và \(x^2-y^2<0\ ↔\ x=0\ và\ y\ne0\). Tập hợp các điểm M là trục Oy trừ O.

b) \({z^2}\) là số ảo khi \(x^2-y^2=0\ ↔\ y=\pm x\). Tập hợp các điểm M là 2 đường phân giác của gốc tọa độ.

c) \({z^2}\) = \((\overline{z})^2\ khi\ xy=0\ ↔\ x=0\ hoặc\ y=0\). Tập hợp các điểm M là 2 trục tọa độ.

d) \(\frac{1}{z-i}=\frac{1}{x+(y-1)i}=\frac{x-(y-1)i}{x^2+(y-1)^2}\) là số ảo khi x = 0, y ≠ 1. Tập hợp M là trục Oy bỏ điểm M(0;1)

16) Tìm nghiệm phức của phương trình sau:

\(a)\ iz+2-i=0\)

\(b) \left( {2 - i} \right)\bar z - 4 = 0\)

\(c) {z^2} + 4 = 0\)

\(d) (2 + 3i)z = z - 1\)

\(e) \left( {iz - 1} \right)\left( {z + 3i} \right)\left( {\bar z - 2 + 3i} \right) = 0\)

\(a)\ z=1+2i\)

\(b) z = - \frac{1}{{10}} + \frac{3}{{10}}i\)

\(c) z = \frac{8}{5} - \frac{4}{5}i\)

\(d)-i-3i;\ 2+3i\)

\(e)\ z=\pm2i\)

17)

a) Cho số phức z = x + yi (x, y ∈R). Khi z ≠ 1, hãy tìm phần thực và phần ảo của số phức \(\frac{{z + i}}{{z - i}}\)

b) Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thỏa điều kiện \(\frac{{z + i}}{{z - i}}\) là số thực dương.

a) Phần thực là \(\frac{{{x^2} + {y^2} - 1}}{{{x^2} + {{(y - 1)}^2}}}\), phần ảo \(\frac{{2x}}{{{x^2} + {{(y - 1)}^2}}}\)

b) Là số thực dương khi x = 0 và \({x^2} + {y^2} - 1 > 0\). Tập hợp là trục Oy bỏ đoạn IJ với I, J là điểm biểu diễn hai số phức i, - i.

18)

a) Trong mặt phẳng phức cho 3 điểm A, B, C không thẳng hàng theo thứ tự biểu diễn số phức \({z_1},\,{z_2},\,{z_3}\). Hỏi trọng tâm DABC biểu diễn số phức nào?

b) Xét 3 điểm A, B, C của mặt phẳng phức theo thứ tự biểu diễn số phức \({z_1},\,{z_2},\,{z_3}\) thỏa mãn \(\left| {{z_1}} \right| = \,\left| {{z_2}} \right| = \left| {\,{z_3}} \right|\). Chứng minh rằng A, B, C là 3 đỉnh của một tam giác đều khi và chỉ khi \({z_1} + \,{z_2} + \,{z_3} = 0\)

a) Gọi G là trọng tâm DABC, ta có:

\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{z_1} + {z_2} + {z_3}} \right)\)

Vậy G biểu diễn số phức \(z = \frac{1}{3}\left( {{z_1} + {z_2} + {z_3}} \right)\)

b) Vì \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right|\) nên A, B, C thuộc đường tròn tâm O. Tam giác ABC đều khi trọng tâm G trùng O hay \({z_1} + \,{z_2} + \,{z_3} = 0.\)

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Công thức giải nhanh cấp số cộng và cấp số nhân. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải. Mời các bạn cùng tham khảo thêm các môn Ngữ văn 12, tiếng Anh 12, đề thi học kì 1 lớp 12, đề thi học kì 2 lớp 12...

Mời các bạn cùng tham khảo thêm các tài liệu:

• Bài tập trắc nghiệm Số phức bài toán Max, Min
• Bài tập trắc nghiệm Số phức dạng quỹ tích
• 50 câu trắc nghiệm số phức (Có đáp án)