Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức

Giá trị lớn nhất, giá trị nhỏ nhất Toán 8

254 433.783

Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức lớp 8

A. Giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức
B. Các bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức
C. Bài tập vận dụng
D. Bộ đề thi giữa kì 1 lớp 8 sách mới:

Tìm giá trị lớn nhất, nhỏ nhất của một biểu thức là dạng bài tập thường xuất hiện trong các bài kiểm tra môn Toán lớp 8. Trong tài liệu dưới đây, VnDoc gửi tới các bạn lý thuyết và một số dạng toán tìm giá trị lớn nhất và nhỏ nhất của biểu thức (biểu thức chứa dấu căn, biểu thức chứa dấu giá trị tuyệt đối,...). Tài liệu giúp các em nắm được cách giải các dạng bài Tìm giá trị nhỏ nhất, lớn nhất của biểu thức. Sau đây mời các bạn tham khảo.

A. Giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức

1. Khái niệm

- Nếu với mọi giá trị của biến thuộc một khoảng xác định nào đó mà giá trị của biểu thức A luôn luôn lớn hơn hoặc bằng (nhỏ hơn hoặc bằng) một hằng số k và tồn tại một giá trị của biến để A có giá trị bằng k thì k gọi là giá trị nhỏ nhất (giá trị lớn nhất) của biểu thức A ứng với các giá trị của biến thuộc khoảng xác định nói trên.

2. Phương pháp

a) Để tìm giá trị nhỏ nhất của A, ta cần:

+ Chứng minh A ≥ k với k là hằng số

+ Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến

b) Để tìm giá trị lớn nhất của A, ta cần:

+ Chứng minh A ≤ k với k là hằng số

+ Chỉ ra dấu “=” có thể xảy ra với giá trị nào đó của biến

Kí hiệu: min A là giá trị nhỏ nhất của A; max A là giá trị lớn nhất của A

B. Các bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức

I. Dạng 1: Tam thức bậc hai

Phương pháp: Đối với dạng tam thức bậc hai ta đưa biểu thức đã cho về dạng bình phương một tổng (hoặc hiệu) cộng (hoặc trừ) đi một số tự do.

Tổng quát:

d - (a ± b)² ≤ d Ta tìm được giá trị lớn nhất
(a ± b)²± c ≥ ± c Ta tìm được giá trị nhỏ nhất

Ví dụ 1: Tìm giá trị lớn nhất của biểu thức B = 6 - 8x - x²

Lời giải

Ta có:

B = 6 - 8x - x² = -(x² + 8x) + 6

= -(x² + 8x + 16) + 6 + 16

= -(x + 4)² + 22

Vì (x +4)² ≥ 0 ⇒ -(x +4)²≤ 0 ⇒ -(x +4)²+ 22 ≤ 22

Do đó, giá trị lớn nhất của biểu thức B là 22

Ví dụ 2. Tìm giá trị nhỏ nhất của biểu thức C = 4x² + 8x + 10

Lời giải

C = 4x² + 8x + 10 = (2x)² + 2.2x.2 + 4 + 6

= (2x + 2)² + 6

Với mọi x ta có: (2x + 2)² ≥ 0 ⇒ (2x + 2)²+ 6 ≥ 6

Do đó, giá trị nhỏ nhất của biểu thức C là 6

Ví dụ 3:

a, Tìm giá trị nhỏ nhất của A = 2x² - 8x + 1

b, Tìm giá trị lớn nhất của B = -5x² - 4x + 1

Lời giải:

a, A = 2(x² - 4x + 4) - 7 = 2(x - 2)² - 7 ≥ -7

min A = -7 khi và chỉ khi x = 2

b, $B = - 5\left( {{x^2} + \frac{4}{5}x} \right) + 1 = - 5\left( {{x^2} - 2.x.\frac{2}{5} + \frac{4}{{25}}} \right) + \frac{9}{5} = \frac{9}{5} - 5{\left( {x + \frac{2}{5}} \right)^2} \le \frac{9}{5}$

max $B = \frac{9}{5} \Leftrightarrow x = - \frac{2}{5}$

Ví dụ 4: Cho tam thức bậc hai P(x) = ax² + bx + c

a, Tìm min P nếu a > 0

b, Tìm max P nếu a < 0

Lời giải:

Ta có $P = a\left( {{x^2} + \frac{b}{a}x} \right) + c = a{\left( {x + \frac{b}{{2a}}} \right)^2} + \left( {c - \frac{{{b^2}}}{{4a}}} \right)$

Đặt $k = c - \frac{{{b^2}}}{{4a}}$ . Do ${\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0$ nên:

a, Nếu a > 0 thì $a{\left( {x + \frac{b}{{2a}}} \right)^2} \ge 0$ do đó P ≥ k ⇒ min P = k

b, Nếu a < 0 thì $a{\left( {x + \frac{b}{{2a}}} \right)^2} \le 0$ do đó P ≤ k ⇒ max P = k ⇒ $x = \frac{{ - b}}{{2a}}$

Bài tập vận dụng

Bài tập: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

a, A = -x² + x + 1	b, B = x² + 3x + 4
c, C = x² - 11x + 30	d, D = x² - 2x + 5
e, E = 3x² - 6x + 4	f, F = -3x² - 12x - 25

II. Dạng 2: Đa thức có dấu giá trị tuyệt đối

Phương pháp: Có hai cách để giải bài toán này:

Cách 1: Dựa vào tính chất |x| ≥ 0. Ta biến đổi biểu thức A đã cho về dạng A ≥ a (với a là số đã biết) để suy ra giá trị nhỏ nhất của A là a hoặc biến đổi về dạng A ≤ b (với b là số đã biết) từ đó suy ra giá trị lớn nhất của A là b.

Cách 2: Dựa vào biểu thức chứa hai hạng tử là hai biểu thức trong dấu giá trị tuyệt đối. Ta sẽ sử dụng tính chất:

∀x, y ∈ $\mathbb{Q}$ ta có:

$\left | x+y \right |\leq\left | x\right | +\left | y\right |$
$\left | x-y \right |\leq\left | x\right | -\left | y\right |$

Ví dụ 1: Tìm giá trị nhỏ nhất của các biểu thức sau:

a. A = (3x - 1)² - 4|3x - 1| + 5

b. B = |x - 2| + |x - 3|

Lời giải:

a, $A = {\left( {3x - 1} \right)^2} - 4\left| {3x - 1} \right| + 5$

Đặt

min A = 1 $\Leftrightarrow y = 2 \Leftrightarrow \left| {3x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 2\\3x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{3}\end{array} \right.$

b, $B = \left| {x - 2} \right| + \left| {x - 3} \right|$

$B = \left| {x - 2} \right| + \left| {x + 3} \right| \ge \left| {x - 2 + 3 - x} \right| = 1$

$\Rightarrow \min B = 1 \Leftrightarrow \left( {x - 2} \right)\left( {3 - x} \right) \ge 0 \Leftrightarrow 2 \le x \le 3$

Ví dụ 2: Tìm giá trị nhỏ nhất của C = |x² - x + 1| + |x² - x - 2|

Hướng dẫn giải

Ta có:

C = |x² - x + 1| + |x² - x - 2| ≥ |x² - x + 1 + 2 + x - x²| = 3

MinC = 3 ⇔ (x² - x + 1)(2 + x - x²) ≥ 0 ⇔ (x + 1)(x - 2) ≤ 0 ⇔ -1 ≤ x ≤ 2

Ví dụ 3: Tìm giá trị nhỏ nhất của T = |x - 1| + |x - 2| + |x - 3| + |x - 4|

Hướng dẫn giải

Ta có |x - 1| + |x - 4| ≥ |x - 1 + 4 - x| = 3 (1)

Và |x - 2| + |x - 3| ≥ |x - 2 +3 - x| = 1(2)

Vậy T ≥ 1 + 3 = 4

Từ (1) suy ra dấu bằng xảy ra khi 1 ≤ x ≤ 4

Từ (2) suy ra dấu bằng xảy ra khi 2 ≤ x ≤ 3

Vậy T có giá trị nhỏ nhất bằng 4 khi 2 ≤ x ≤ 3

Bài tập vận dụng: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức dưới đây:

A = |x - 2004| + |x - 2005|

B = |x - 2| + |x - 9| + 1945

C = -|x - 7| - |y + 13| + 1945

III. Dạng 3: Đa thức bậc cao

Dạng phân thức
Phân thức có tử là hằng số, mẫu là tam thức bậc hai
Các phân thức có dạng khác

Ví dụ 1: Tìm giá trị nhỏ nhất của các đa thức sau:

a. A = x(x - 3)(x - 4)(x - 7)

b. B = 2x² + y² - 2xy - 2x + 3

c. C = x² + xy + y² - 3x - 3

Lời giải:

a, A = x(x - 3)(x - 4)(x - 7) = (x² - 7x)(x² - 7x + 12)

Đặt y = x² - 7x + 6 thì A = (y - 6)(y + 6) = y² - 36 ≥ -36

Min $A = - 36 \Leftrightarrow y = 0 \Leftrightarrow {x^2} + 7x + 6 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = 6 \end{array} \right.$

b, B = 2x² + y² - 2xy - 2x + 3 = (x² - 2xy + y2) + (x² - 2x + 1) + 2

$= {\left( {x - y} \right)^2} + {\left( {x - 1} \right)^2} + 2 \ge 2 \Leftrightarrow \left\{ \begin{array}{l} x - y = 0\\ x - 1 = 0 \end{array} \right. \Leftrightarrow x = y = 1$

c, C = x² + xy + y² - 3x - 3 = x² - 2x + y² - 2y + xy - x - y

Ta có $C + 3 = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 2y + 1} \right) + \left( {xy - x - y + 1} \right)$

$= {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + \left( {x - 1} \right)\left( {y - 1} \right)$ Đặt thì

$C + 3 = {a^2} + {b^2} + ab = \left( {{a^2} + 2.a.\frac{b}{2} + \frac{{{b^2}}}{4}} \right) + \frac{{3{b^2}}}{4} = {\left( {a + \frac{b}{2}} \right)^2} + \frac{{3{b^2}}}{4} \ge 0$

Vậy Min(C + 3) = 0 hay min C = -3⇔ a = b = 0 ⇔ x = y = 1

C. Bài tập vận dụng

1. Bài tập trắc nghiệm

Câu 1. Tìm giá trị lớn nhất của biểu thức B = 10 - x2

A.0 B.10 C. -10 D. 9

Đáp án

Ta có: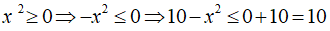

Do đó, giá trị lớn nhất của biểu thức B là 10

Chọn B.

Câu 2. Tìm giá trị lớn nhất của biểu thức A = 4x - 2x2

A.0

B. 1

C. 4

D. 2

Đáp án

Ta có;

A = 4x - 2x2 = -2(x2 - 2x)

= -2(x2 - 2x + 1) + 2 = -2(x - 1)2 + 2

Vì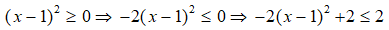

Do đó, giá trị lớn nhất của biểu thức A là 2.

Chọn D.

Câu 3 . Tìm giá trị lớn nhất của biểu thức C = 4x + 3 - x2

A.7

B. 4

C. 3

D. -1

Đáp án

Ta có:

Vì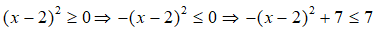

Do đó, giá trị lớn nhất của C là 7.

Chọn A.

Câu 4. Tìm giá trị lớn nhất của biểu thức D = -x2 + 6x - 11

A.-11 B. 6 C. -2 D. 9

Đáp án

D = -x2 + 6x - 11 = -(x2 - 6x) - 11

= -(x2 - 6x + 9) + 9 - 11

= -(x - 3)2 - 2

Vì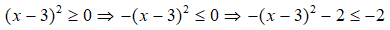

Giá trị lớn nhất của biểu thức D là – 2

Chọn C

Câu 5. Tìm giá trị lớn nhất của biểu thức E = 4x - x2 + 1

A.1 B. 5 C. 3 D. 6

Đáp án

Ta có:

E = 4x - x2 + 1 = -(x2 - 4x) + 1

= -(x2 - 4x + 4) + 4 + 1

= -(x - 2)2 + 5

Vì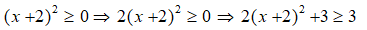

Do đó, giá trị lớn nhất của biểu thức E là 5.

Chọn B.

Câu 6. Tìm giá trị nhỏ nhất của biểu thức A = 2x2 + 8x + 11

A.3 B. 8 C. 11 D. 9

Đáp án

Ta có:

A = 2x2 + 8x + 11 = 2(x2 + 4x) + 11

= 2(x2 + 4x + 4) - 8 + 11

= 2(x + 2)2 + 3

Vì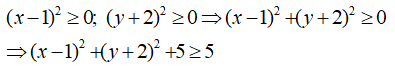

Vậy giá trị nhỏ nhất của biểu thức A là 3

Chọn A.

Câu 7. Tìm giá trị nhỏ nhất của biểu thức E = x2 - 2x + y2 + 4y + 10

A.1 B. 10 C. 5 D. 8

Đáp án

Ta có:

E = x2 - 2x + y2 + 4y + 10

= (x2 - 2x + 1) + (y2 + 4y + 4) + 5

= (x - 1)2 + (y + 2)2 + 5

Vì

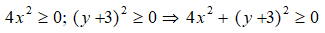
Do đó, giá trị nhỏ nhất của E là 5.

Chọn C.

Câu 8. Tìm giá trị nhỏ nhất của biểu thức D = 4x2 + y2 + 6y + 20

A. 20 B. 11 C. 10 D. 16

Đáp án

Ta có;

D = 4x2 + y2 + 6y + 20 = 4x2 + (y2 + 6y + 9) + 11

= 4x2 + (y + 3)2 + 11

Vì: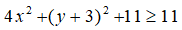

Suy ra:

Vậy giá trị nhỏ nhất của D là 11

Chọn B.

Câu 9. Tìm giá trị nhỏ nhất của biểu thức G = x2 + 5y2 - 4xy - 8y + 28

A.10 B. 8 C. 20 D. 15

Đáp án

Ta có:

G = x2 + 5y2 - 4xy - 8y + 28

G = (x2 - 4xy + 4y2) + (y2 - 8y + 16) + 8

= (x - 2y)2 + (y - 4)2 + 8

Vì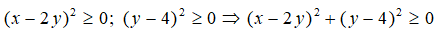

Suy ra: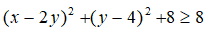

Vậy giá trị nhỏ nhất của G là 8.

Chọn B.

2. Bài tập tự luận:

Bài tập 1: Tìm giá trị nhỏ nhất của biểu thức:

a, $A = 2{x^2} + 2xy + {y^2} - 2x + 2y + 2$

b, $B = {x^4} - 8xy + {x^3}y + {x^2}{y^2} - x{y^3} + {y^4} + 200$

c, $C = {x^2} + xy + {y^2} - 3x - 3y$

d, $D = x\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)$

Bài tập 2: Tìm giá trị lớn nhất của biểu thức:

$A = - {x^2} - {y^2} + xy + 2x + 2y$

--------------------------------

D. Bộ đề thi giữa kì 1 lớp 8 sách mới:

Toán 8 từ năm học 2023 - 2024 trở đi sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Việc lựa chọn giảng dạy bộ sách nào sẽ tùy thuộc vào các trường. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc sẽ cung cấp lời giải bài tập sách giáo khoa, sách bài tập, trắc nghiệm toán từng bài và các tài liệu giảng dạy, học tập khác. Mời các bạn tham khảo qua đường link bên dưới:

Tham khảo thêm

Đánh giá bài viết

254 433.783

Chia sẻ bởi:
Công chúa Tuyết
Nhóm:
Sưu tầm
Ngày: 30/10/2023

Tải về Bản in

3 Bình luận

Sắp xếp theo

Xóa Đăng nhập để Gửi

Đoàn Việt Hưng giải chi tiết xem nào
Thích Phản hồi 6 13/10/20
Bé Heo
khá hữu ích
Thích Phản hồi 1 04/11/22
Loi Doan
có 1 chỗ bị sai

Thích Phản hồi 6 10/08/21
- Quỳnhh Zyy
  vd3 câu b đk? 9/5 ko hiểu nó ra từ đâu
  Thích Phản hồi 0 09:21 21/03