Đề cương ôn tập học kì 1 môn Toán lớp 11
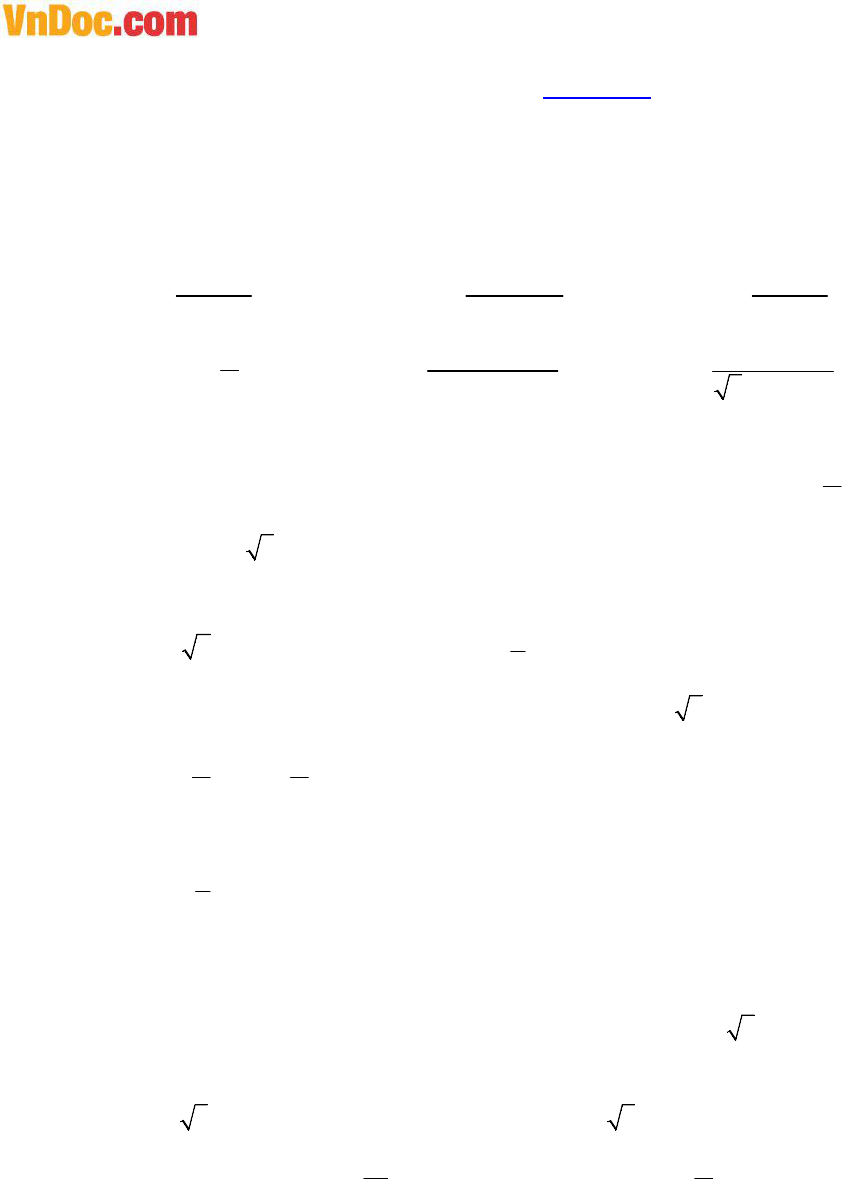


Nội dung ôn thi học kì I môn Toán lớp 11
Đề cương ôn tập học kì 1 môn Toán lớp 11 vừa được VnDoc.com sưu tập và xin gửi tới bạn đọc để bạn đọc cùng tham khảo và có thêm tài liệu ôn tập. Đề cương gồm có 9 trang gồm kiến thức các phần Đại số và Hình học trong toán 11 học kì 1, phía cuối là một số đề thi tham khảo. Mời bạn đọc cùng tham khảo chi tiết bài viết dưới đây nhé.
ĐỀ CƯƠNG ÔN TẬP TOÁN 11
HỌC KÌ 1 – CHUẨN VÀ NÂNG CAO
I. HÀM SỐ LƯỢNG GIÁC – PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Tìm tập xác định của mỗi hàm số sau đây:
a. ![]() \(f\left( x \right)=\frac{\sin x+1}{\sin x-1}\)
\(f\left( x \right)=\frac{\sin x+1}{\sin x-1}\)
Điều kiện xác định:
![]() \(\sin x-1\ne 0\Rightarrow \sin x\ne 1\Rightarrow x\ne \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\)
\(\sin x-1\ne 0\Rightarrow \sin x\ne 1\Rightarrow x\ne \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\)
Vậy tập xác định của hàm số là: ![]() \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \right\}\)
\(D=\mathbb{R}\backslash \left\{ \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \right\}\)
b. ![]() \(f\left( x \right)=\frac{2\tan x+2}{\cos x-1}\)
\(f\left( x \right)=\frac{2\tan x+2}{\cos x-1}\)
Điều kiện xác định của hàm số:
![]() \(\cos x-1\ne 0\Rightarrow \cos x\ne 1\Rightarrow x\ne k2\pi ,k\in \mathbb{Z}\)
\(\cos x-1\ne 0\Rightarrow \cos x\ne 1\Rightarrow x\ne k2\pi ,k\in \mathbb{Z}\)
Vậy tập xác định của hàm số là: ![]() \(D=\mathbb{R}\backslash \left\{ k2\pi ,k\in \mathbb{Z} \right\}\)
\(D=\mathbb{R}\backslash \left\{ k2\pi ,k\in \mathbb{Z} \right\}\)
c. ![]() \(f\left( x \right)=\frac{\cot x}{\sin x+1}\)
\(f\left( x \right)=\frac{\cot x}{\sin x+1}\)
Điều kiện xác định của hàm số là:
![]() \(\sin x+1\ne 0\Rightarrow \sin x\ne -1\Rightarrow x\ne \frac{-\pi }{2}+k2\pi ,k\in \mathbb{Z}\)
\(\sin x+1\ne 0\Rightarrow \sin x\ne -1\Rightarrow x\ne \frac{-\pi }{2}+k2\pi ,k\in \mathbb{Z}\)
Vậy tập xác định của hàm số là: ![]() \(D=\mathbb{R}\backslash \left\{ -\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \right\}\)
\(D=\mathbb{R}\backslash \left\{ -\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \right\}\)
d.  \(y=\tan \left( x+\dfrac{\pi }{3} \right)=\frac{\sin \left( x+\dfrac{\pi }{3} \right)}{\cos \left( x+\dfrac{\pi }{3} \right)}\)
\(y=\tan \left( x+\dfrac{\pi }{3} \right)=\frac{\sin \left( x+\dfrac{\pi }{3} \right)}{\cos \left( x+\dfrac{\pi }{3} \right)}\)
Điều kiện xác định của hàm số:
![]() \(\cos \left( x+\frac{\pi }{3} \right)\ne 0\Rightarrow x+\frac{\pi }{3}\ne \frac{\pi }{2}+k\pi \Rightarrow x\ne \frac{\pi }{6}+k\pi ,k\in \mathbb{Z}\)
\(\cos \left( x+\frac{\pi }{3} \right)\ne 0\Rightarrow x+\frac{\pi }{3}\ne \frac{\pi }{2}+k\pi \Rightarrow x\ne \frac{\pi }{6}+k\pi ,k\in \mathbb{Z}\)
Vậy tập xác định của hàm số là: ![]() \(D=\mathbb{R}\backslash \left\{ \frac{\pi }{6}+k\pi ,k\in \mathbb{Z} \right\}\)
\(D=\mathbb{R}\backslash \left\{ \frac{\pi }{6}+k\pi ,k\in \mathbb{Z} \right\}\)
2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a. ![]() \(y=3\cos x+2\)
\(y=3\cos x+2\)
Ta có:
 \(\begin{align} & -1\le \cos x\le 1 \\ & \Rightarrow -3\le 3\cos x\le 3 \\ & \Rightarrow -1\le 3\cos x+2\le 5 \\ & \Rightarrow -1\le y\le 5 \\ \end{align}\)
\(\begin{align} & -1\le \cos x\le 1 \\ & \Rightarrow -3\le 3\cos x\le 3 \\ & \Rightarrow -1\le 3\cos x+2\le 5 \\ & \Rightarrow -1\le y\le 5 \\ \end{align}\)
Giá trị lớn nhất của hàm số là:
![]() \(\max y=5\Leftrightarrow \cos x=1\Rightarrow x=k2\pi ,k\in \mathbb{Z}\)
\(\max y=5\Leftrightarrow \cos x=1\Rightarrow x=k2\pi ,k\in \mathbb{Z}\)
Giá trị nhỏ nhất của hàm số là:
![]() \(\min y=-1\Leftrightarrow \cos x=-1\Rightarrow x=\pi +k2\pi ,k\in \mathbb{Z}\)
\(\min y=-1\Leftrightarrow \cos x=-1\Rightarrow x=\pi +k2\pi ,k\in \mathbb{Z}\)
b. ![]() \(y=1-5\sin 3x\)
\(y=1-5\sin 3x\)
Ta có:
 \(\begin{align} & -1\le \sin 3x\le 1 \\ & \Rightarrow 5\ge -5\sin 3x\ge -5 \\ & \Rightarrow 6\ge 1-5\sin 3x\ge -4 \\ & \Rightarrow 6\ge y\ge -4 \\ \end{align}\)
\(\begin{align} & -1\le \sin 3x\le 1 \\ & \Rightarrow 5\ge -5\sin 3x\ge -5 \\ & \Rightarrow 6\ge 1-5\sin 3x\ge -4 \\ & \Rightarrow 6\ge y\ge -4 \\ \end{align}\)
Giá trị lớn nhất của hàm số là:
![]() \(\Rightarrow \max y=6\Leftrightarrow \sin 3x=-1\Rightarrow x=\frac{-\pi }{6}+\frac{k2\pi }{3},k\in \mathbb{Z}\)
\(\Rightarrow \max y=6\Leftrightarrow \sin 3x=-1\Rightarrow x=\frac{-\pi }{6}+\frac{k2\pi }{3},k\in \mathbb{Z}\)
Giá trị nhỏ nhất của hàm số là:
![]() \(\Rightarrow \min y=-4\Leftrightarrow \sin 3x=1\Rightarrow x=\frac{\pi }{6}+\frac{k2\pi }{3},k\in \mathbb{Z}\)
\(\Rightarrow \min y=-4\Leftrightarrow \sin 3x=1\Rightarrow x=\frac{\pi }{6}+\frac{k2\pi }{3},k\in \mathbb{Z}\)
c. ![]() \(y=4\cos \left( 2x+\frac{\pi }{5} \right)+9\)
\(y=4\cos \left( 2x+\frac{\pi }{5} \right)+9\)
Tương tự câu trên ta dễ dàng chỉ ra
![]() \(\begin{align} & \Rightarrow 5\le y\le 13 \\ \end{align}\)
\(\begin{align} & \Rightarrow 5\le y\le 13 \\ \end{align}\)
Giá trị lớn nhất của hàm số là:
![]() \(\max y=13\Leftrightarrow \cos \left( 2x+\frac{\pi }{5} \right)=1\Rightarrow x=-\frac{\pi }{10}+k\pi ,k\in \mathbb{Z}\)
\(\max y=13\Leftrightarrow \cos \left( 2x+\frac{\pi }{5} \right)=1\Rightarrow x=-\frac{\pi }{10}+k\pi ,k\in \mathbb{Z}\)
Giá trị nhỏ nhất của hàm số là:
![]() \(\min y=5\Leftrightarrow \cos \left( 2x+\frac{\pi }{5} \right)=-1\Rightarrow x=\frac{4\pi }{10}+k\pi ,k\in \mathbb{Z}\)
\(\min y=5\Leftrightarrow \cos \left( 2x+\frac{\pi }{5} \right)=-1\Rightarrow x=\frac{4\pi }{10}+k\pi ,k\in \mathbb{Z}\)
d.
 \(\begin{align} & f\left( x \right)=\cos x-\sqrt{3}\sin x=2\left( \frac{1}{2}.\cos x-\frac{\sqrt{3}}{2}.\sin x \right) \\ & =2.\left( \cos \left( \frac{\pi }{3} \right).\cos x-\sin \left( \frac{\pi }{3} \right).\sin x \right)=2\cos \left( x+\frac{\pi }{3} \right) \\ \end{align}\)
\(\begin{align} & f\left( x \right)=\cos x-\sqrt{3}\sin x=2\left( \frac{1}{2}.\cos x-\frac{\sqrt{3}}{2}.\sin x \right) \\ & =2.\left( \cos \left( \frac{\pi }{3} \right).\cos x-\sin \left( \frac{\pi }{3} \right).\sin x \right)=2\cos \left( x+\frac{\pi }{3} \right) \\ \end{align}\)
Ta có:
 \(\begin{align} & -1\le \cos \left( x+\frac{\pi }{3} \right)\le 1\Rightarrow -2\le 2\cos \left( x+\frac{\pi }{3} \right)\le 2 \\ & \Rightarrow -2\le y\le 2 \\ \end{align}\)
\(\begin{align} & -1\le \cos \left( x+\frac{\pi }{3} \right)\le 1\Rightarrow -2\le 2\cos \left( x+\frac{\pi }{3} \right)\le 2 \\ & \Rightarrow -2\le y\le 2 \\ \end{align}\)
Giá trị lớn nhất của hàm số là:
![]() \(\Rightarrow \max y=2\Leftrightarrow \cos \left( x+\frac{\pi }{3} \right)=1\Rightarrow x=-\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}\)
\(\Rightarrow \max y=2\Leftrightarrow \cos \left( x+\frac{\pi }{3} \right)=1\Rightarrow x=-\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}\)
Giá trị nhỏ nhất của hàm số là:
![]() \(\Rightarrow \min y=-2\Leftrightarrow \cos \left( x+\frac{\pi }{3} \right)=-1\Rightarrow x=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}\)
\(\Rightarrow \min y=-2\Leftrightarrow \cos \left( x+\frac{\pi }{3} \right)=-1\Rightarrow x=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}\)
f.
 \(\begin{align} & f(x)={{\sin }^{4}}x+{{\cos }^{4}}x={{\left( {{\sin }^{2}}x+{{\cos }^{2}}x \right)}^{2}}-2{{\sin }^{2}}x.{{\cos }^{2}}x \\ & =1-\frac{1}{2}{{\sin }^{2}}2x=1-\frac{1}{2}\frac{1-\cos 4x}{2}=\frac{3}{4}+\frac{\cos 4x}{4} \\ \end{align}\)
\(\begin{align} & f(x)={{\sin }^{4}}x+{{\cos }^{4}}x={{\left( {{\sin }^{2}}x+{{\cos }^{2}}x \right)}^{2}}-2{{\sin }^{2}}x.{{\cos }^{2}}x \\ & =1-\frac{1}{2}{{\sin }^{2}}2x=1-\frac{1}{2}\frac{1-\cos 4x}{2}=\frac{3}{4}+\frac{\cos 4x}{4} \\ \end{align}\)
Ta có:
 \(\begin{align} & -1\le \cos 4x\le 1 \\ & \Rightarrow \frac{-1}{4}\le \frac{\cos 4x}{4}\le \frac{1}{4} \\ & \Rightarrow \frac{1}{2}\le \frac{3}{4}+\frac{\cos 4x}{4}\le 1 \\ & \Rightarrow \frac{1}{2}\le y\le 1 \\ \end{align}\)
\(\begin{align} & -1\le \cos 4x\le 1 \\ & \Rightarrow \frac{-1}{4}\le \frac{\cos 4x}{4}\le \frac{1}{4} \\ & \Rightarrow \frac{1}{2}\le \frac{3}{4}+\frac{\cos 4x}{4}\le 1 \\ & \Rightarrow \frac{1}{2}\le y\le 1 \\ \end{align}\)
Giá trị lớn nhất của hàm số là:
![]() \(\max y=1\Leftrightarrow \cos 4x=1\Rightarrow x=\frac{k\pi }{2},k\in \mathbb{Z}\)
\(\max y=1\Leftrightarrow \cos 4x=1\Rightarrow x=\frac{k\pi }{2},k\in \mathbb{Z}\)
Giá trị nhỏ nhất của hàm số là:
![]() \(\min y=-1\Leftrightarrow \cos 4x=-1\Rightarrow x=\frac{\pi }{4}+\frac{k\pi }{2},k\in \mathbb{Z}\)
\(\min y=-1\Leftrightarrow \cos 4x=-1\Rightarrow x=\frac{\pi }{4}+\frac{k\pi }{2},k\in \mathbb{Z}\)
1.3. Giải phương trình lượng giác cơ bản:
Hướng dẫn giải
a.  \(2\sin x+\sqrt{2}=0\Rightarrow \sin x=\dfrac{-\sqrt{2}}{2}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{4}+k2\pi \\ x=\pi +\dfrac{\pi }{4}+k2\pi \\ \end{matrix}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{4}+k2\pi \\ x=\dfrac{5\pi }{4}+k2\pi \\ \end{matrix} \right. \right.,k\in \mathbb{Z}\)
\(2\sin x+\sqrt{2}=0\Rightarrow \sin x=\dfrac{-\sqrt{2}}{2}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{4}+k2\pi \\ x=\pi +\dfrac{\pi }{4}+k2\pi \\ \end{matrix}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{4}+k2\pi \\ x=\dfrac{5\pi }{4}+k2\pi \\ \end{matrix} \right. \right.,k\in \mathbb{Z}\)
Vậy phương trình có nghiệm ![]() \(x=\frac{-\pi }{4}+k2\pi\) hoặc
\(x=\frac{-\pi }{4}+k2\pi\) hoặc ![]() \(x=\frac{5\pi }{4}+k2\pi ,k\in \mathbb{Z}\)
\(x=\frac{5\pi }{4}+k2\pi ,k\in \mathbb{Z}\)
b.
 \(\sin \left( x-2 \right)=\frac{2}{3}\Rightarrow \left[ \begin{matrix} x-2=\arcsin \dfrac{2}{3}+k2\pi \\ x-2=\pi -\arcsin \dfrac{2}{3}+k2\pi \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{matrix} x=\arcsin \dfrac{2}{3}+2+k2\pi \\ x=\pi -\arcsin \dfrac{2}{3}+2+k2\pi \\ \end{matrix} \right.,k\in \mathbb{Z}\)
\(\sin \left( x-2 \right)=\frac{2}{3}\Rightarrow \left[ \begin{matrix} x-2=\arcsin \dfrac{2}{3}+k2\pi \\ x-2=\pi -\arcsin \dfrac{2}{3}+k2\pi \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{matrix} x=\arcsin \dfrac{2}{3}+2+k2\pi \\ x=\pi -\arcsin \dfrac{2}{3}+2+k2\pi \\ \end{matrix} \right.,k\in \mathbb{Z}\)
Vậy phương trình có nghiệm ![]() \(x=\pi -\arcsin \frac{2}{3}+2+k2\pi\) hoặc
\(x=\pi -\arcsin \frac{2}{3}+2+k2\pi\) hoặc ![]() \(x=\arcsin \frac{2}{3}+2+k2\pi ,k\in \mathbb{Z}\)
\(x=\arcsin \frac{2}{3}+2+k2\pi ,k\in \mathbb{Z}\)
c. ![]() \(\cot \left( x+{{20}^{o}} \right)=\cot {{60}^{o}}\)
\(\cot \left( x+{{20}^{o}} \right)=\cot {{60}^{o}}\)
Điều kiện: ![]() \(\sin \left( x+{{20}^{o}} \right)\ne 0\Rightarrow x+{{20}^{0}}\ne k\pi \Rightarrow x\ne -{{20}^{0}}+k\pi ,k\in \mathbb{Z}\)
\(\sin \left( x+{{20}^{o}} \right)\ne 0\Rightarrow x+{{20}^{0}}\ne k\pi \Rightarrow x\ne -{{20}^{0}}+k\pi ,k\in \mathbb{Z}\)
Phương trình tương đương:
![]() \(x+{{20}^{0}}={{60}^{0}}+k\pi \Rightarrow x={{40}^{0}}+k\pi ,k\in \mathbb{Z}\)
\(x+{{20}^{0}}={{60}^{0}}+k\pi \Rightarrow x={{40}^{0}}+k\pi ,k\in \mathbb{Z}\)
Vậy phương trình có nghiệm ![]() \(x={{40}^{0}}+k\pi ,k\in \mathbb{Z}\)
\(x={{40}^{0}}+k\pi ,k\in \mathbb{Z}\)
d. ![]() \(2\cos 2x+1=0\Rightarrow \cos 2x=\frac{-1}{2}\Rightarrow x=\pm \frac{2\pi }{6}+k\pi ,k\in \mathbb{Z}\)
\(2\cos 2x+1=0\Rightarrow \cos 2x=\frac{-1}{2}\Rightarrow x=\pm \frac{2\pi }{6}+k\pi ,k\in \mathbb{Z}\)
Vậy phương trình có nghiệm ![]() \(x=\pm \frac{2\pi }{6}+k\pi ,k\in \mathbb{Z}\)
\(x=\pm \frac{2\pi }{6}+k\pi ,k\in \mathbb{Z}\)
Các câu còn lại học sinh tự giải
1.4. Giải các phương trình lượng giác sau đây:
Hướng dẫn giải
a.
 \(\begin{align} & {{\cos }^{2}}2x=\frac{1}{4}\Leftrightarrow 4{{\cos }^{2}}2x=1\Leftrightarrow 2.\left( \cos 4x+1 \right)=1 \\ & \Leftrightarrow 2.\cos 4x=-1\Leftrightarrow \cos 4x=\frac{-1}{2}\Leftrightarrow x=\pm \frac{2\pi }{12}+\frac{k\pi }{2},k\in \mathbb{Z} \\ \end{align}\)
\(\begin{align} & {{\cos }^{2}}2x=\frac{1}{4}\Leftrightarrow 4{{\cos }^{2}}2x=1\Leftrightarrow 2.\left( \cos 4x+1 \right)=1 \\ & \Leftrightarrow 2.\cos 4x=-1\Leftrightarrow \cos 4x=\frac{-1}{2}\Leftrightarrow x=\pm \frac{2\pi }{12}+\frac{k\pi }{2},k\in \mathbb{Z} \\ \end{align}\)
b.
 \(\begin{align} & 4{{\cos }^{2}}2x-3=0\Rightarrow 2.\left( \cos 4x+1 \right)-3=0\Rightarrow 2.\cos 4x-1=0 \\ & \Rightarrow \cos 4x=\frac{1}{2}\Rightarrow x=\pm \frac{\pi }{12}+k2\pi ,k\in \mathbb{Z} \\ \end{align}\)
\(\begin{align} & 4{{\cos }^{2}}2x-3=0\Rightarrow 2.\left( \cos 4x+1 \right)-3=0\Rightarrow 2.\cos 4x-1=0 \\ & \Rightarrow \cos 4x=\frac{1}{2}\Rightarrow x=\pm \frac{\pi }{12}+k2\pi ,k\in \mathbb{Z} \\ \end{align}\)
Vậy phương trình có nghiệm: ![]() \(x=\pm \frac{\pi }{12}+k2\pi ,k\in \mathbb{Z}\)
\(x=\pm \frac{\pi }{12}+k2\pi ,k\in \mathbb{Z}\)
1.5. Tìm các nghiệm của phương trình sau trong khoảng đã cho:
a/ 2sin2x + 1 = 0 với 0 < x < π
b/ cot(x - 5) = √3 với -π < x < π
Hướng dẫn giải
a.  \(2\sin 2x+1=0\Leftrightarrow \sin 2x=\frac{-1}{2}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{3}+k\pi \\ x=\dfrac{5\pi }{6}+k\pi \\ \end{matrix} \right.,k\in \mathbb{Z}\)
\(2\sin 2x+1=0\Leftrightarrow \sin 2x=\frac{-1}{2}\Rightarrow \left[ \begin{matrix} x=\dfrac{-\pi }{3}+k\pi \\ x=\dfrac{5\pi }{6}+k\pi \\ \end{matrix} \right.,k\in \mathbb{Z}\)
Do phương trình có nghiệm nằm trong khoảng ![]() \(\left( 0,\pi \right)\) nên ta xét các trường hợp như sau:
\(\left( 0,\pi \right)\) nên ta xét các trường hợp như sau:
Với ![]() \(x=\frac{-\pi }{3}+k\pi\) ta có:
\(x=\frac{-\pi }{3}+k\pi\) ta có:
![]() \(0 < x< \pi \Leftrightarrow 0<\frac{-\pi }{3}+k\pi < \pi \Leftrightarrow \frac{1}{3}< k< \frac{4}{3},k\in \mathbb{Z}\Rightarrow k=1\Rightarrow x=\frac{2\pi }{3}\)
\(0 < x< \pi \Leftrightarrow 0<\frac{-\pi }{3}+k\pi < \pi \Leftrightarrow \frac{1}{3}< k< \frac{4}{3},k\in \mathbb{Z}\Rightarrow k=1\Rightarrow x=\frac{2\pi }{3}\)
Với ![]() \(x=\frac{5\pi }{6}+k\pi\)
\(x=\frac{5\pi }{6}+k\pi\)
![]() \(0< x<\pi \Leftrightarrow 0<\frac{5\pi }{6}+k\pi < \pi \Leftrightarrow \frac{-5}{6}< k <\frac{1}{6},k\in \mathbb{Z}\Rightarrow k=0\Rightarrow x=\frac{5\pi }{6}\)
\(0< x<\pi \Leftrightarrow 0<\frac{5\pi }{6}+k\pi < \pi \Leftrightarrow \frac{-5}{6}< k <\frac{1}{6},k\in \mathbb{Z}\Rightarrow k=0\Rightarrow x=\frac{5\pi }{6}\)
Vậy trên khoảng ![]() \(\left( 0,\pi \right)\) phương trình có nghiệm
\(\left( 0,\pi \right)\) phương trình có nghiệm ![]() \(x=\frac{2\pi }{3},x=\frac{5\pi }{6}\)
\(x=\frac{2\pi }{3},x=\frac{5\pi }{6}\)
1. 6. Giải các phương trình sau:
![]() \(a.{{\cos }^{2}}x-\sqrt{3}\sin x\cos x=0\)
\(a.{{\cos }^{2}}x-\sqrt{3}\sin x\cos x=0\)
![]() \(b.\sqrt{3}\cos x+\sin 2x=0\)
\(b.\sqrt{3}\cos x+\sin 2x=0\)
![]() \(c.8\sin x.\cos x.\cos 2x=\cos 8\left( \frac{\pi }{16}-x \right)\)
\(c.8\sin x.\cos x.\cos 2x=\cos 8\left( \frac{\pi }{16}-x \right)\)
![]() \(d.{{\sin }^{4}}\left( x+\frac{\pi }{2} \right)-{{\sin }^{4}}x=\sin 4x\)
\(d.{{\sin }^{4}}\left( x+\frac{\pi }{2} \right)-{{\sin }^{4}}x=\sin 4x\)
1. 7. Giải phương trình:
![]() \(a.\cos 7x.\cos x=\cos 5x.\cos 3x\)
\(a.\cos 7x.\cos x=\cos 5x.\cos 3x\)
![]() \(b.\cos 4x+\sin 3x.\cos x=\sin x.\cos 3x\)
\(b.\cos 4x+\sin 3x.\cos x=\sin x.\cos 3x\)
![]() \(c.1+\cos x+\cos 2x+\cos 3x=0\)
\(c.1+\cos x+\cos 2x+\cos 3x=0\)
![]() \(d.{{\sin }^{2}}x+{{\sin }^{2}}2x+{{\sin }^{2}}3x+{{\sin }^{2}}4x=2\)
\(d.{{\sin }^{2}}x+{{\sin }^{2}}2x+{{\sin }^{2}}3x+{{\sin }^{2}}4x=2\)
1. 8. Giải phương trình:
![]()
1. 9. Giải phương trình:
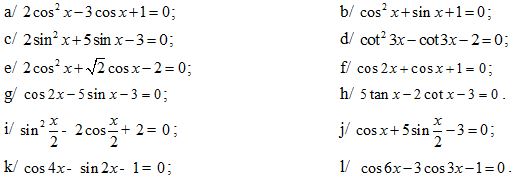
1. 10. Giải các phương trình:
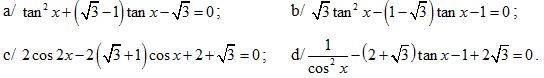
1. 11. Giải phương trình:

1. 12. Giải phương trình:

1. 13. Giải phương trình:
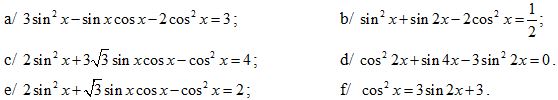
II. TỔ HỢP – XÁC SUẤT
2. 1. Có bao nhiêu số tự nhiên có hai chữ số mà hai chữ số của nó đều chẵn?
2. 2. Từ các chữ số 0, 1, 2, 3, 4, 5, 6, có thể tạo nên bao nhiêu số tự nhiên có hai chữ số khác nhau?
2. 3. Từ các chữ số 2, 3, 4, 6, 7 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
2. 4. Cho tập hợp X = {0, 1, 2, 3, 4, 5, 6, 7, 8}. Từ các phần tử của tập X có thể lập bao nhiêu số tự nhiên trong các trường hợp sau:
a/ Số đó có 4 chữ số khác nhau từng đôi một.
b/ Số đó là số chẵn và có 4 chữ số khác nhau từng đôi một.
2. 5. Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau và chia hết cho 5?
2. 6. Có tối đa bao nhiêu số máy điện thoại có 7 chữ số bắt đầu bằng số 8 sao cho:
a/ Các chữ số đôi một khác nhau.
b/ Các chữ số tùy ý.
2. 7. a/ Có bao nhiêu cách chọn 3 người từ 10 người để thực hiện cùng một công việc?
b/ Có bao nhiêu cách chọn 3 người từ 10 người để thực hiện ba công việc khác nhau?
2. 8. Trong một cuộc thi có 16 đội tham dự, giả sử rằng không có hai đội nào cùng điểm.
a/ Nếu kết quả cuộc thi là chọn ra ba đội có điểm cao nhất thì có bao nhiêu cách chọn?
b/ Nếu kết quả cuộc thi là chọn ra các giải nhất, nhì, ba thì có bao nhiêu sự lựa chọn?
2. 9. Từ các chữ số 2, 3, 4, 5, 6, 7, 8 có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau và lớn hơn 8600?
2. 10. Cho 10 điểm nằm trên một đường tròn.
a/ Có bao nhiêu đoạn thẳng mà hai đầu là hai trong số 10 điểm đã cho?
b/ Có bao nhiêu vectơ khác ![]() có gốc và ngọn trùng với hai trong số 10 điểm đã cho?
có gốc và ngọn trùng với hai trong số 10 điểm đã cho?
c/ Có bao nhiêu tam giác mà các đỉnh là ba trong số 10 điểm đã cho?
Mời các bạn tải file đầy đủ về tham khảo.
Trên đây VnDoc.com vừa giới thiệu tới bạn đọc Đề cương ôn tập học kì 1 môn Toán lớp 11, chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết tổng hợp lại toàn bộ nội dung lý thuyết và các bài tập kèm theo trong học kì 1.... Mong rằng qua đây bạn đọc có thêm thật nhiều tài liệu và tổng hợp được kiến thức môn Toán để ôn tập tốt hơn nhé. Để giúp bạn đọc có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời bạn đọc cùng tham khảo thêm một số tài liệu học tập các môn được chúng tôi biên soạn và tổng hợp tại các mục sau Ngữ văn 11, Tiếng Anh 11, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11...


