Đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12 năm học 2017 - 2018, Sở GD&ĐT Hòa Bình
VnDoc xin giới thiệu tới bạn đọc tài liệu: Đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12 năm học 2017 - 2018, Sở GD&ĐT Hòa Bình, với bộ câu hỏi bài tập kèm theo lời giải chi tiết sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán 12 một cách hiệu quả hơn. Mời các bạn tham khảo.
Đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12
Chi tiết đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12
Câu 1: (3,0 điểm):
a) Tìm các điểm cực trị của đồ thị hàm số f (x) = 1+ 3x2 - 2x3.
b) Tìm điều kiện của tham số m để đồ thị hàm số ![]() \(y\ =\frac{2x\ -\sqrt{mx^2+1}}{\left(x-1\right)^2}\)
\(y\ =\frac{2x\ -\sqrt{mx^2+1}}{\left(x-1\right)^2}\)
Câu 2 (5,0 điểm):
a) Tính tổng các nghiệm x ∈ [- \(\pi\) ;
\(\pi\) ; \(\pi\) ] của phương trình: 2(cosx +
\(\pi\) ] của phương trình: 2(cosx + ![]() \(\sqrt{3}\) sin x) cos x = cos x -
\(\sqrt{3}\) sin x) cos x = cos x - ![]() \(\sqrt{3}\) sinx + 1
\(\sqrt{3}\) sinx + 1
b) Giải phương trình (3 +![]() \(\sqrt{5}\))x +(3 -
\(\sqrt{5}\))x +(3 - ![]() \(\sqrt{5}\))x -7.2x = 0.
\(\sqrt{5}\))x -7.2x = 0.
c) Giải hệ phương trình
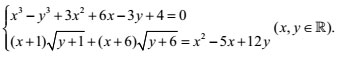
Đề thi học sinh giỏi lớp 12 môn Văn năm học 2017 - 2018 tỉnh Hải Dương
Đề thi học sinh giỏi môn Ngữ văn lớp 12 trường THPT Lý Thái Tổ, Bắc Ninh năm học 2017 - 2018
Đề thi học sinh giỏi lớp 12 môn Sinh học năm học 2017 - 2018 tỉnh Hải Dương
Đề thi học sinh giỏi lớp 12 môn Toán năm học 2017 - 2018 tỉnh Hải Dương
Đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12 năm học 2017 - 2018, Sở GD&ĐT Thái Bình
---------------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Đề thi chọn đội tuyển HSG cấp tỉnh môn Toán lớp 12 năm học 2017 - 2018, Sở GD&ĐT Hòa Bình. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Sinh học, Thi thpt Quốc gia môn Văn, đề thi học kì 2 lớp 12, Thi thpt Quốc gia môn Lịch sử mà VnDoc tổng hợp và đăng tải.





