Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Công thức tính nhanh bán kính mặt cầu ngoại tiếp, ngoại tiếp hình khối

Công thức Toán 12

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Công thức bán kính mặt cầu ngoại tiếp, nội tiếp Toán 12

Bài viết Công thức tính nhanh bán kính mặt cầu ngoại tiếp, ngoại tiếp hình khối – Công thức Toán 12 sẽ giúp bạn hệ thống hóa các công thức quan trọng, trình bày phương pháp áp dụng và mẹo giải nhanh trong từng dạng bài thường gặp. Thông qua các ví dụ minh họa, học sinh lớp 12 có thể rút ngắn thời gian làm bài và nâng cao độ chính xác khi xử lý các bài toán hình học không gian.

Mặt cầu ngoại tiếp đa diện

Mặt cầu đi qua tất cả các đỉnh của đa diện.

Các đa diện thường gặp có mặt cầu ngoại tiếp: Hình chóp có đáy là: tam giác, hình chữ nhật, hình thang cân và đa giác đều (tam giác đều, hình vuông, ngũ giác đều, lục giác đều, …).

Lăng trụ đứng và có đáy là các hình như trên.

Mặt cầu nội tiếp đa diện

Mặt cầu tiếp xúc với tất cả các mặt của đa diện.

Bán kính khối cầu ngoại tiếp hình lập phương

$R = \frac{cạ{nh}_{hình\ lập\ phương}\sqrt{3}}{2}$

Bán kính khối cầu nội tiếp hình lập phương

$R = \frac{cạ{nh}_{hình\ lập\ phương}}{2}$

Lưu ý: $AC' = A'C = BD' = B'D = cạnh\sqrt{3}$

Bán kinh khối cầu ngoại tiếp hình hộp chữ nhật hoặc khối chóp có ba cạnh đôi một vuông góc

$R = \frac{1}{2}\sqrt{\left( cạ{nh}_{1} \right)^{2} + \left( cạ{nh}_{2} \right)^{2} + \left( cạ{nh}_{3} \right)^{2}}$

Bán kính khối cầu ngoại tiếp lăng trụ đứng

$\ R = \sqrt{\left( \frac{{cao}_{lăng\ trụ}}{2} \right)^{2} + \left( bán\ kính\ đáy_{ngoại\ tiếp} \right)^{2}}$

Bán kính khối cầu ngoại tiếp hình chóp có SA vuông góc với đáy hoặc lăng trụ đứng:

$R = \sqrt{\left( \frac{{cao}_{hình\ chóp}}{2} \right)^{2} + \left( bán\ kính\ đáy_{ngoại\ tiếp} \right)^{2}}$

Bán kính khối cầu ngoại tiếp hình chóp đều

$\ R = \frac{(cạnh\ bên)^{2}}{2cao};\ \ R = \frac{(cạnh\ bên)^{2}}{2\sqrt{(cạnh\ bên)^{2} - \left( bán\ kính\ đáy_{ngoại\ tiếp} \right)^{2}}}$

Với cách tìm bán kính đáy là:

$r_{nội_{tam\ giác\ đều}} = \frac{cạnh\sqrt{3}}{6}$

$r_{ngoại_{tam\ giác\ đều}} = \frac{cạnh\sqrt{3}}{3}$ $r_{nội_{hình\ vuông}} = \frac{cạnh}{2}$

$r_{ngoại_{hình\ vuông}} = \frac{cạnh\sqrt{2}}{2}$

$r_{ngoại_{tam\ giác\ vuông}} = \frac{huyền}{2}$

$r_{ngoại_{hình\ chữ\ nhật}} = \frac{chéo_{hình\ chữ\ nhật}}{2}$

Ví dụ. Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a?

Hướng dẫn giải

Dựng hình

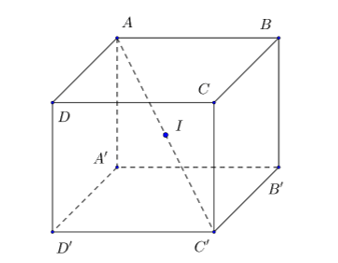
Gọi I là trung điểm A thì I cách đều các đỉnh A, B, C, D, , , , , ta dễ dàng chứng minh được:

IA = IB = IC = ID = IA' = IB' =
IC' = ID'

Vậy I là tâm mặt cầu ngoại tiếp hình lập phương. Bán kính mặt cầu là :

$R = IA = \frac{AC'}{2} = \frac{\sqrt{AB^{2} + AD^{2}\text{+A}\text{A}^{'2}}}{2} = \frac{AB\sqrt{3}}{2} = \frac{a\sqrt{3}}{2}$

Lưu ý: do khoảng cách từ I đến sáu mặt của hình lập phương bằng nhau và bằng $\frac{AB}{2}$ nên I cũng là tâm mặt cầu nội tiếp hình lập phương.

Ví dụ. Cho tứ diện có ba đường thẳng , , vuông góc với nhau từng đôi một, , , . Tính diện tích mặt cầu ngoại tiếp ?

Hướng dẫn giải

Cách 1: Dựng hình

Bước 1: Xác định tâm đường tròn ngoại tiếp đa giác đáy

Xét hình chóp có đáy là tam giác vuông SBC và đường cao SA.

Gọi I là tâm đường tròn ngoại tiếp tam giác đáy SBC.

Do SB vuông góc SC nên tam giác SBC vuông tại S.

$\Rightarrow$ I là trung điểm cạnh huyền BC

Bước 2: Dựng trục đường tròn ngoại tiếp của đa giác đáy.

Kẻ đường thẳng d qua điểm I và vuông góc mặt phẳng (SBC), khi đó đường thẳng d được gọi là trục đường tròn ngoại tiếp tam giác SBC.

$SA\bot(SBC) \Rightarrow SA \parallel d$ . Với mọi điểm O nằm trên d, ta có $OS = OB = OC\ (1)$ .

Bước 3: Dựng tâm mặt cầu ngoại tiếp hình chóp

Gọi M là trung điểm SA, kẻ $MO\bot d$ $(O \in d) \Rightarrow$ MO là đường trung trực của đoạn thẳng SA

$\Rightarrow OS = OA\ (2)$ .

Từ $\ (1)\ và\ \ (2),\ \ OS = OA = OB = OC$ nên O cách đều các điểm S, A, B, C. Hay O được gọi là tâm mặt cầu ngoại tiếp chóp S.ABC với bán kính .

Bước 4: Tìm bán kính mặt cầu

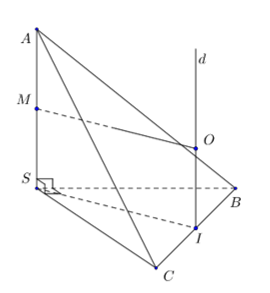
Với O là tâm mặt cầu được xác định, bán kính mặt cầu là đoạn thẳng OS

$R = SO = \sqrt{OI^{2} + SI^{2}} = \sqrt{SM^{2} + \left( \frac{BC}{2} \right)^{2}}$

$= \sqrt{\left( \frac{SA}{2} \right)^{2} + \frac{BC^{2}}{4}} = \sqrt{\frac{SA}{4}^{2} + \frac{SB^{2} + SC^{2}}{4}}$

$= \frac{1}{2}\sqrt{SA^{2} + SB^{2} + SC^{2}} = \frac{1}{2}\sqrt{3^{2} + 4^{2} + 5^{2}} = \frac{5\sqrt{2}}{2}$

Ví dụ. Tính bán kính của mặt cầu ngoại tiếp tứ diện đều cạnh bằng ?

Hướng dẫn giải

Dựng hình

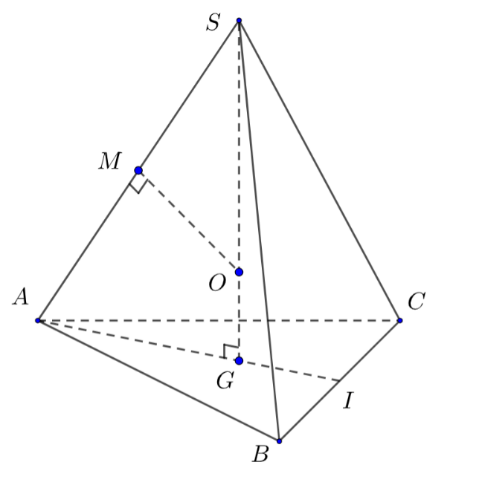
Bước 1: Xác định tâm đường tròn ngoại tiếp đa giác đáy

Tứ diện đều nên có đã giác đáy tam giác ABC là tam giác đều.

Vậy tâm đường tròn ngoại tiếp tam giác ABC là điểm G với G là trọng tâm tác giác ABC.

Bước 2: Dựng trục đường tròn ngoại tiếp của đa giác đáy.

Do tứ diện S.ABC là tứ diện đều nên $SG\bot(ABC)$ , vậy SG là trục đường tròn ngoại tiếp tam giác ABC.

Với điểm O bất kỳ nằm trên SG thì $OA = OB = OC\ (1)$ .

Bước 3: Dựng tâm mặt cầu ngoại tiếp hình chóp

Xét cạnh bên SA có trung điểm M. Trong mặt phẳng , dựng đường trung trực đoạn thẳng SA đi qua M và cắt SG tại điểm O. Khi đó $\text{OS} = OA$ .

Từ $\ (1)\ và\ \ (2),\ OS = OA = OB = OC$ nên O cách đều các điểm S, A, B, C.

Hay O được gọi là tâm mặt cầu ngoại tiếp tứ diện đều S.ABC với bán kính .

Bước 4: Tìm bán kính mặt cầu

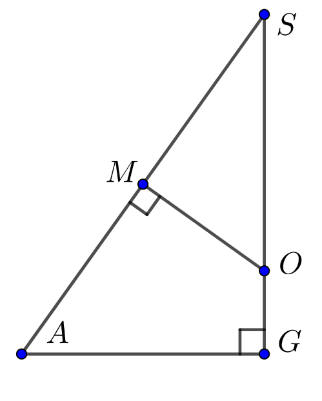
Xét hai tam giác đồng dạng SAG và SMO có:

$\frac{SO}{SA} = \frac{SM}{SG}$

$\Rightarrow SO = \frac{SA.SM}{SG} = \frac{SA.\frac{SA}{2}}{\sqrt{SA^{2} - AG^{2}}} = \frac{SA^{2}}{2\sqrt{SA^{2} - AG^{2}}}$

Do tam giác ABC là tam giác đều cạnh a nên

$AG = \frac{AB\sqrt{3}}{3} =\frac{a\sqrt{3}}{3}$

$\Rightarrow R = SO = \frac{SA^{2}}{2\sqrt{SA^{2} - AG^{2}}} = \frac{a^{2}}{2\sqrt{a^{2} - \left( \frac{a\sqrt{3}}{3} \right)^{2}}} = \frac{\sqrt{6}}{4}$ .

🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.

---------------------------------------------------------

Chuyên đề công thức tính nhanh bán kính mặt cầu ngoại tiếp hình khối giúp học sinh hiểu sâu hơn về mối liên hệ giữa hình học không gian và các công thức Toán 12 quan trọng. Khi nắm vững công thức và phương pháp áp dụng, học sinh sẽ dễ dàng nhận diện dạng toán và lựa chọn cách giải phù hợp.

Tải về

Chọn file muốn tải về: