Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Khoảng cách từ một điểm đến một đường thẳng trong không gian Oxyz

Khoảng cách giữa hai đường thẳng chéo nhau

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Công thức tính khoảng cách điểm đến đường thẳng trong Oxyz

Trong chương trình Toán 12, dạng toán khoảng cách từ một điểm đến một đường thẳng trong không gian Oxyz và khoảng cách giữa hai đường thẳng chéo nhau là nội dung quan trọng, thường xuất hiện trong đề thi THPT Quốc gia môn Toán. Việc nắm chắc công thức và phương pháp giải giúp học sinh xử lý bài toán nhanh và chính xác hơn.

Công thức tính khoảng cách từ một điểm đến một đường thẳng

Khoảng cách từ điểm M đến một đường thẳng dqua điểm M_o có vectơ chỉ phương $\overrightarrow{u}$ :

$d(M,d) = \frac{\left| \left\lbrack \overrightarrow{M_{0}M};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|}$

Công thức tính khoảng cách giữa hai đường thẳng

Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia.

Công thức tính khoảng cách giữa hai đường thẳng chéo nhau

Đường thẳng d đi qua điểm M và có vectơ chỉ phương $\overrightarrow{u}$ và d’ đi qua điểm M’ và có vectơ chỉ phương $\overrightarrow{u'}$ là:

$d(d,d') = \frac{\left| \left\lbrack \overrightarrow{u};\overrightarrow{u'} \right\rbrack.\overrightarrow{M_{0}M} \right|}{\left| \left\lbrack \overrightarrow{u};\overrightarrow{u'} \right\rbrack \right|}$

Khoảng cách từ giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm thuộc đường thẳng đến mặt phẳng hoặc khoảng cách từ một điểm thuộc mặt phẳng đến đường thẳng.

Bài tập minh họa tính khoảng cách từ điểm đến đường thẳng

Ví dụ. Trong không gian cho điểm và đường thẳng $d:\frac{x - 5}{2} = \frac{y - 1}{3} = \frac{z - 2}{- 2}$ . Điểm thuộc đường thẳng sao cho cách một khoảng bằng $\sqrt{17}$ . Tọa độ điểm là

A. và $(6;\ \ 9;\ \ 2)$ . B. và

C. và D. và

Hướng dẫn giải

Cách 1: Ta có:

$M(5 + 2t;1 + 3t;2 - 2t) \in d$ ; $\overrightarrow{AM}(2 + 2m;3 + 3m; - 2 - 2m)$

$\Rightarrow AM = \sqrt{17} \Leftrightarrow 17(1 + m)^{2} = 17$

$\Leftrightarrow \left\lbrack \begin{matrix} m = 0 \\ m = - 2 \end{matrix} \right.\ \Rightarrow \left\lbrack \begin{matrix} M(5;1;2) \\ M(1; - 5;6) \end{matrix} \right.$

Cách 2: Kiểm tra các điểm thuộc đường thẳng có 2 cặp điểm trong đáp án B và C thuộc đường thẳng . Dùng công thức tính độ dài suy ra đáp án C thỏa mãn.

Ví dụ. Trong không gian với hệ trục toạ độ cho 2 điểm $A(1;5;\ 0);\ B(3;\ 3;\ 6)$ và đường thẳng $d:\frac{x + 1}{2} = \frac{y - 1}{- 1} = \frac{z}{2}$ . Gọi là điểm trên đường thẳng sao cho diện tích tam giác nhỏ nhất. Khoảng cách giữa 2 điểm và là

A. B. $\sqrt{29}.$ C. $\sqrt{33}.$ D.

Hướng dẫn giải:

Hình vẽ minh họa:

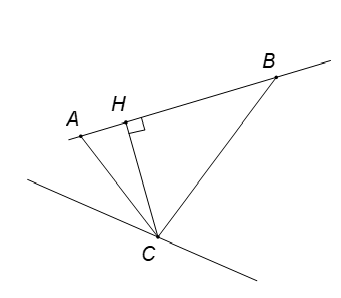
Ta có 2 đường thẳng và chéo nhau.

Gọi là điểm trên và là hình chiếu vuông góc của trên đường thẳng .

Vì $S_{ABC}\ = \ \frac{1}{2}AB \cdot \ CH\ = \ \sqrt{11} \cdot \ CH$ nên $S_{ABC}$ nhỏ nhất khi nhỏ nhất $\Leftrightarrow CH$ là đoạn vuông góc chung của 2 đường thẳng và .

Ta có $C(1;\ \ 0;\ \ 2)\ \Rightarrow \ AC\ = \ \sqrt{29}$ .

📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.

-----------------------------------------------------

Chuyên đề khoảng cách từ một điểm đến đường thẳng trong không gian Oxyz giúp học sinh hiểu rõ công thức và cách áp dụng trong Toán 12. Luyện tập thường xuyên dạng toán này sẽ giúp bạn nâng cao kỹ năng giải toán và tự tin hơn trong kỳ thi THPT Quốc gia môn Toán.

Xem thử Tải về

Chọn file muốn tải về: