Đề thi giải toán trên Máy tính cầm tay lớp 12 tỉnh Bến Tre năm 2012 - 2013 môn Toán

Vndoc.com xin giới thiệu đến các bạn: Đề thi giải toán trên Máy tính cầm tay lớp 12 tỉnh Bến Tre năm 2012 - 2013 môn Toán.

Đề thi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẾN TRE ĐỀ THI CHÍNH THỨC

ĐỀ THI GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY CẤP TỈNH NĂM HỌC 2012 - 2013 MÔN THI: TOÁN - LỚP 12 Ngày thi: 23/01/2013 Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Bài 1:

Đồ thị hàm số y = ax⁴ + bx³ + cx² + d đi qua bốn điểm A(-2; -32); B(0; -4); C(1; 5) và D(3; 113).

1. Xác định giá trị của a, b, c, d

2. Tìm tọa độ gần đúng các điểm cực trị của đồ thị hàm số.

Bài 2:

Cho dãy số {x_n} với n = 1, 2, 3,... thỏa mãn x₁ = 1,49999999 và x_n+1 = 2x_n³ - 5x_n² + 4x_n với n = 1, 2, 3,...

1. Chứng minh rằng dãy ố có giói hạn hữu hạn.

2. Tìm giá trị nhỏ nhất của n để cho |x_n - 1| < 10^-7

Bài 3:

Tìm gần đúng giá trị lớn nhất và nhỏ nhất của hàm số:

Bài 4:

Tìm nghiệm gần đúng của hệ phương trình: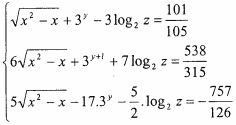

Bài 5:

Cho dãy số {u_n} được xác định như sau: u1 = 2; u2 = 5;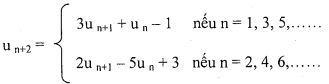

1. Viết quy trình bấm phím liên tục tính giá trị của u8; u12; u16 của dãy.

2. Gọi Sn là tổng của n số hạng đầu tiên của dãy. Tính S10; S15; S20

Bài 6:

Cho hình tư diện SABC. Gọi G là trọng tâm tam giác SBC, mặt phẳng (P) đi qua A, G cắt SB, SC lần lượt tại M, N.

1. Chứng minh hệ thức: x + y = 3xy

2. Gọi V1, V lần lượt là thể tích tứ diện SAMN, SABC. Tìm tập giá trị của V1/V khi x thay đổi.