Đề thi giữa kì 1 Toán 8 năm 2021 - 2022 (đề 4)

Đề kiểm tra giữa kì 1 Toán 8 có đáp án

Đề thi giữa kì 1 Toán 8 năm 2021 đề 4

Đề thi giữa kì 1 Toán 8 năm 2021 - 2022 (đề 4) được VnDoc sưu tầm và đăng tải. Đề thi giữa học kì 1 lớp 8 môn Toán này là tài liệu tham khảo hữu ích dành cho thầy cô trong quá trình giảng dạy, ôn luyện kiến thức đã học cho các em học sinh đồng thời cũng giúp học sinh làm quen nhiều dạng đề kiểm tra Toán lớp 8 khác nhau. Mời các em cùng tham khảo

Phòng Giáo dục và Đào tạo .....

Đề thi Giữa kì 1

Môn: Toán lớp 8

Thời gian làm bài: 90 phút

(Đề 4)

Câu 1 (2 điểm) Phân tích đa thức thành nhân tử

a. 8x² - 8xy - 4x + 4y b. x³ + 10x² + 25x - xy²

c. x² + x - 6 d. 2x² + 4x - 16

Câu 2 (2 điểm) Tìm giá trị của x, biết:

a. x³ - 16x = 0 b. (2x + 1)² - (x - 1)² = 0

Câu 3 (2 điểm) Chứng minh biểu thức sau không phụ thuộc vào x

a. A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

b. B = x(2x + 1) - x²(x + 2) + x³ - x + 5

Câu 4 (1 điểm) Tính giá trị nhỏ nhất của biểu thức P = x² - 2xy + 6y² - 12x + 2y + 45

Câu 5 (2 điểm) Cho hình thang ABDC (AB // CD). Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Từ M và N kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự E và F. Chứng minh rằng:

a. BE = EF = FD

b. Cho CD = 8cm, ME = 6cm. Tính độ dài AB và FN

Câu 6 (0.5 điểm) Cho x, y, z là các số dương. Tìm giá trị nhỏ nhất của:

$P=(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)$ $P=(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)$

Đáp án và Hướng dẫn làm bài

Câu 1:

a. 8x² - 8xy - 4x + 4y = 8x(x - y) - 4(x - y) = (x - y)(8x - 4) = 4(x - y)(2x - 1)

b.

x³ + 10x² + 25x - xy² = x(x² + 10x + 25 - y²) = x[(x - 5)² - y²] = x(x - 5 - y)(x - 5 + y)

c. x² + x - 6 = x² - 2x + 3x - 6 = x(x - 2) + 3(x - 2) = (x - 2)(x + 3)

d.

2x² + 4x - 16 = 2(x² - 2x - 8) = 2(x² - 2x + 1 - 9)

= 2[(x - 1)² - 9] = 2(x - 1 - 9)(x - 1 + 9) = 2(x - 10)(x + 8)

Câu 2:

a.

x³ - 16x = 0

x(x² - 16) = 0

x(x - 4)(x + 4) = 0

Suy ra x = 0, x = 4, x = -4

b.

(2x + 1)² - (x - 1)² = 0

(2x + 1 - x + 1)(2x + 1 + x - 1) = 0

(x + 2)(3x) = 0

Suy ra x = 0 hoặc x = -2

Câu 3:

a.

A = (2x - 1)(4x² + 2x + 1) - (2x + 1)(4x² - 2x + 1)

A = (2x)³ - 1 - [(2x)³ + 1]

A = 8x³ - 1 - 8x³ - 1

A = -2

Vậy giá trị của biểu thức A không phụ thuôc vào giá trị của x.

b.

B = x(2x + 1) - x²(x + 2) + x³ - x + 5

B = 2x² + x - x³ - 2x² + x³ - x + 5

B = 5

Vậy biểu thức không phụ thuộc vào x

Câu 4:

$\begin{aligned} &P=x^{2}-2 x y+6 y^{2}-12 x+2 y+45 \\ &P=x^{2}+y^{2}+36-2 x y-12 x+12 y+5 y^{2}-10 y+5+4 \\ &P=(x-y-6)^{2}+5(y-1)^{2}+4 \end{aligned}$ $\begin{aligned} &P=x^{2}-2 x y+6 y^{2}-12 x+2 y+45 \\ &P=x^{2}+y^{2}+36-2 x y-12 x+12 y+5 y^{2}-10 y+5+4 \\ &P=(x-y-6)^{2}+5(y-1)^{2}+4 \end{aligned}$

Do $\left\{\begin{array}{c} (x-y-6)^{2} \geq 0 \\ (y-1)^{2} \geq 0 \end{array}, \forall x, y\right.$ $\left\{\begin{array}{c} (x-y-6)^{2} \geq 0 \\ (y-1)^{2} \geq 0 \end{array}, \forall x, y\right.$

$\Rightarrow P\geqslant 4$ $\Rightarrow P\geqslant 4$

Vậy giá trị nhỏ nhất của biểu thức P là 4 khi và chỉ khi x = 7 và y = 1

Câu 5:

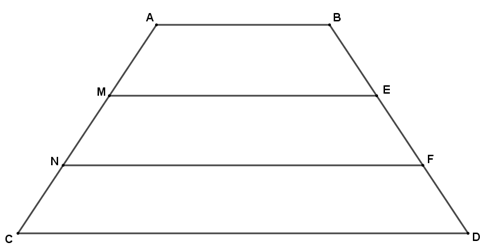
Đề thi giữa kì 1 Toán 8 năm 2021 - 2022 (đề 4)

a. Ta có ABCD là hình thang AB // CD

Ta có AB // CD, FN // CD suy ra AB // NF

Vậy ABFN là hình thang (dấu hiệu nhận biết).

Xét hình thang ABFN có ME // NF, ME = NF nên ME là đường trung bình của hình thang ABFN

Suy ra BE = EF.

Xét tương tự với hình thang MEDC ta suy ra EF = FD

Ta có điều phải chứng minh.

b. Theo chứng minh trên ta có

Vì NF là đường trung bình của hình thang MEDC nên ta có:

$N F=\frac{1}{2}(M E+C D)=\frac{1}{2}(6+8)=7 \mathrm{~cm}$ $N F=\frac{1}{2}(M E+C D)=\frac{1}{2}(6+8)=7 \mathrm{~cm}$

Vì ME là đường trung bình của hình thang ABFN

Suy ra: $M E=\frac{1}{2}(A B+N F) \Rightarrow A B=2 M E-N F=2.6-7=5 \mathrm{~cm}$ $M E=\frac{1}{2}(A B+N F) \Rightarrow A B=2 M E-N F=2.6-7=5 \mathrm{~cm}$

Câu 6:

$P=(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1$ $P=(x+y+z)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1$

$=3+\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)$ $=3+\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)$

Mặt khác $\left(\frac{x}{y}+\frac{y}{x}\right) \geq 2$ $\left(\frac{x}{y}+\frac{y}{x}\right) \geq 2$với mọi số dương x, y nên

P = 3 + 2 + 2 + 2 = 9

Vậy giá trị nhỏ nhất của P là 9 khi x = y = z

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 8. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Như vậy VnDoc đã chia sẻ tới các em Đề thi giữa kì 1 Toán 8 năm 2021 - 2022 (đề 4). Hy vọng với tài liệu này sẽ giúp ích cho các em hệ thống lại những kiến thức đã học trong bài, định hướng phương pháp giải các bài tập cụ thể. Ngoài ra việc tham khảo tài liệu còn giúp các em học sinh rèn luyện và nâng cao kỹ năng giải đề thi. Chúc các em ôn tập tốt, để ôn thi tốt hơn các em nên làm thêm nhiều đề thi giữa học kì 1 tại link bên cạnh này nhé: Đề thi giữa kì 1 lớp 8

............................................

Ngoài Đề thi giữa kì 1 Toán 8 năm 2021 - 2022 (đề 4). Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 8, đề thi học kì 2 lớp 8 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

1

1.028