VnDoc.com

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020

Đề kiểm tra học HK2 môn Toán lớp 9 có đáp án

Bài trước

Bài sau

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm 2020

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020. Được VnDoc sưu tầm và đăng tải, kèm lời giải chi tiết cho các bạn đánh giá so sánh, hy vọng tài liệu này sẽ giúp ích cho các bạn học tốt môn Toán lớp 9 này. Mời các bạn cùng tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

A. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm):

Học sinh chọn chữ cái đứng trước câu trả lời đúng và ghi vào tờ giấy làm bài kiểm tra

Câu 1: Điểm A(1;2) thuộc đồ thị hàm số nào?

$B.\ y=-x^2$ $B.\ y=-x^2$

$C.\ y=x^2$ $C.\ y=x^2$

$D.\ y=-2x^2$ $D.\ y=-2x^2$

Câu 2: Gọi $x1, x2$ là 2 nghiệm của phương trình: $x^2 - 5x + 4 = 0$, ta có:

$A. x_1+x_2 = -5;x_1x_2 = 4$

$B.\ x_1+x_2 = 5;x_1x_2 =- 4$ $B.\ x_1+x_2 = 5;x_1x_2 =- 4$

$C.\ x_1+x_2 = 5;x_1x_2 = 4$ $C.\ x_1+x_2 = 5;x_1x_2 = 4$

$D.\ x_1+x_2 = -5;x_1x_2 = -4$ $D.\ x_1+x_2 = -5;x_1x_2 = -4$

Câu 3: Trong hình 1, số đo góc AOB bằng:

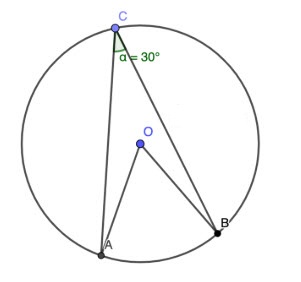
Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020

A. 30°

B. 60°

C. 15°

D. 45°

Câu 4: Cho tứ giác ABCD nội tiếp đường tròn (O), biết ∠A = 115°; ∠B = 75°. Thì ∠C và ∠D có số đo là:

A. ∠C = 105°; ∠D = 65°

B. ∠C = 115°; ∠D = 65°

C. ∠C = 65°; ∠D = 115°

D. ∠C = 65°; ∠D = 105°

B. PHẦN TỰ LUẬN (8,0 điểm)

Câu 1 (2,0 điểm). Giải phương trình và hệ phương trình sau:

$a)\ x^2 + 3x + 2 = 0$ $a)\ x^2 + 3x + 2 = 0$

$b)\ x^4 - 3x^2 - 4 = 0$ $b)\ x^4 - 3x^2 - 4 = 0$

$c)\ \left\{ \matrix{ 3x + y = 5 \hfill \cr 2x + y =4 \hfill \cr} \right.$ $c)\ \left\{ \matrix{ 3x + y = 5 \hfill \cr 2x + y =4 \hfill \cr} \right.$

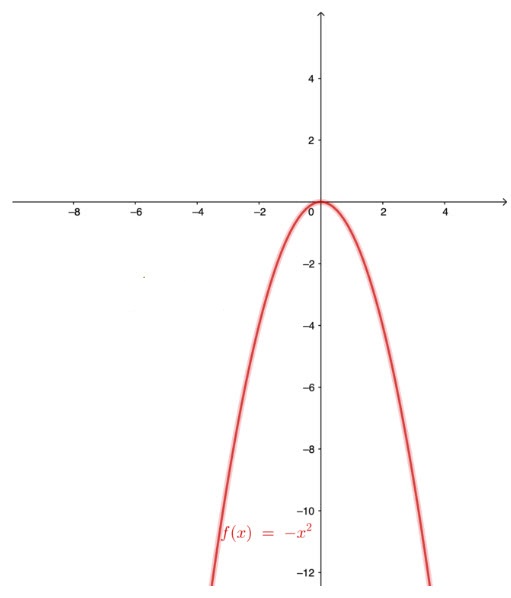
Câu 2 (1,0 điểm). Vẽ đồ thị hàm số $y=-x^2$

Câu 3 (2,0 điểm). Cho phương trình bậc hai:

$x^2 - 2(m+2)x+m^2 + 7 =0\ (1)$ $x^2 - 2(m+2)x+m^2 + 7 =0\ (1)$

(m là tham số).

a) Giải phương trình (1) khi m = 1.

b) Tìm m để phương trình (1) có hai nghiệm $x1, x2$ thoả mãn:

$x_1x_2 - 2(x_1+x_2) = 4$

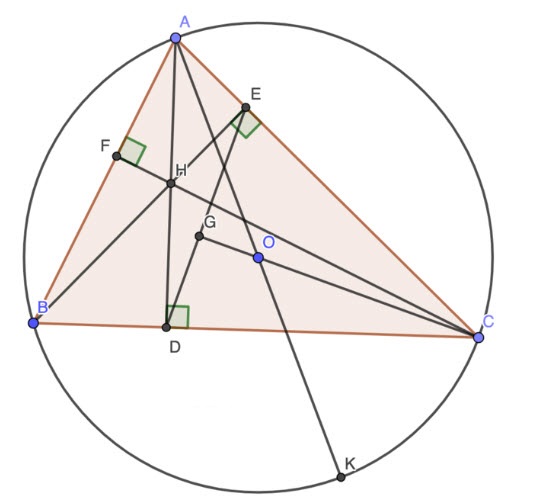
Câu 4 (3,0 điểm)

Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn (O). Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.

a) Chứng minh rằng AEHF là tứ giác nội tiếp.

b) Vẽ đường kính AK của đường tròn (O). Chứng minh AB.AC = AK.AD.

c) Chứng minh rằng OC vuông góc với DE.

Hết

Đáp án đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm 2020

A. PHẦN TRẮC NGHIỆM KHÁCH QUAN

Câu 1. A

Câu 2. C

Câu 3. B

Câu 4. D

B. PHẦN TỰ LUẬN

Câu 1 (2,0 điểm).

$a)\ x^2 + 3x + 2 = 0$ $a)\ x^2 + 3x + 2 = 0$

$\Leftrightarrow (x+2)(x+1) = 0$ $\Leftrightarrow (x+2)(x+1) = 0$

$\Leftrightarrow \left[ \matrix{ x=-1 \hfill \cr x=-2 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x=-1 \hfill \cr x=-2 \hfill \cr} \right.$

$b)\ x^4 - 3x^2 - 4 = 0$ $b)\ x^4 - 3x^2 - 4 = 0$

$\Leftrightarrow (x^2-4)(x^2+1) = 0$ $\Leftrightarrow (x^2-4)(x^2+1) = 0$

$\Leftrightarrow x^2 = 4 \Leftrightarrow x =±2$ $\Leftrightarrow x^2 = 4 \Leftrightarrow x =±2$

$c)\ \left\{ \matrix{ 3x + y = 5 \hfill \cr 2x + y =4 \hfill \cr} \right.$ $c)\ \left\{ \matrix{ 3x + y = 5 \hfill \cr 2x + y =4 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x=1 \hfill \cr y=2 \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ x=1 \hfill \cr y=2 \hfill \cr} \right.$

Câu 2 (1,0 điểm). Vẽ đồ thị hàm số $y=-x^2$

Các em kẻ bảng giá trị rồi vẽ hình:

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020

Câu 3 (2,0 điểm).

a)

Với m = 1, ta có:

$(1) \Leftrightarrow x^2 - 2(1+2)x+1^2 + 7 =0$ $(1) \Leftrightarrow x^2 - 2(1+2)x+1^2 + 7 =0$

$\Leftrightarrow x^2 - 6x+8 =0$ $\Leftrightarrow x^2 - 6x+8 =0$

$\Leftrightarrow \left[ \matrix{ x=4 \hfill \cr x=2 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x=4 \hfill \cr x=2 \hfill \cr} \right.$

b)

Phương trình (1) có hai nghiệm khi:

$\Delta$ $\Delta' = (m+2)^2 -m^2-7 = 4m -3 \geq 0 \Leftrightarrow m \geq \dfrac{3}4$

Áp dụng hệ thức Vi-ét cho (1), ta có:

$\left\{ \matrix{ x_1+x_2 = 2(m+2) \hfill \cr x_1x_2 =m^2+7 \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = 2(m+2) \hfill \cr x_1x_2 =m^2+7 \hfill \cr} \right.$

Thay vào biểu thức $x_1x_2 - 2(x_1+x_2) = 4$, có:

$m^2+7 - 4(m+2) = 4$

$\Leftrightarrow m^2-4m -5 = 0$ $\Leftrightarrow m^2-4m -5 = 0$

$\Leftrightarrow \left[ \matrix{ m=5 \hfill \cr m=-1 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ m=5 \hfill \cr m=-1 \hfill \cr} \right.$

Kết hợp với điều kiện để phương trình có nghiệm $m \geq \dfrac{3}4 \Rightarrow m = 5.$ $m \geq \dfrac{3}4 \Rightarrow m = 5.$

Kết luận....

Câu 4 (3,0 điểm)

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020

a)

Vì BE, CF là đường cao của △ABC ⇒ BE ⊥ AC và CF ⊥ AB hay ∠AFH = ∠AEH = 90°

Suy ra E, F cùng thuộc đường tròn đường kính AH, hay tứ giác AEHF nội tiếp (đpcm).

b)

Vì AK là đường kính $⇒ ∠ACK = 90° = ∠ADB$ (góc nội tiếp chắn đường kính)

Vì 4 điểm A,B,K,C cùng thuộc đường tròn $(O) ⇒ ∠ABD = ∠AKC$ (góc nội tiếp cùng chắn cung AC)

Xét △ABD và △AKC có:

$∠ACK = ∠ADB (cmt)$

$∠ABD = ∠AKC (cmt)$

Suy ra $△ABD ∽ △AKC ⇒ \dfrac{AB}{AD} = \dfrac{AK}{AC} ⇒ AB.AC = AK.AD (đpcm).$ $△ABD ∽ △AKC ⇒ \dfrac{AB}{AD} = \dfrac{AK}{AC} ⇒ AB.AC = AK.AD (đpcm).$

c)

Lấy điểm G là giao điểm của OC với EF.

Vì $△ABD ∽ △AKC (cmt) ⇒ ∠BAD = ∠KAC = ∠OCA$ (do △OAC cân tại O)

Vì ∠AFB = ∠ADB = 90° ⇒ Tứ giác AEDB nội tiếp ⇒ ∠ABD = 180° - ∠AED = ∠DEC

Xét △EGC, có:

$∠EGC = 180° - ∠GCE - ∠GEC = 180° - ∠OCA - ∠DEC$

$= 180° - ∠BAD - ∠ABD = ∠ADB = 90°$

Suy ra CG ⊥ GE hay CO ⊥ DE (đpcm).

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020 được VnDoc chia sẻ trên đây. Đây là đề cương hay giúp các bạn học sinh củng cố kiến thức Toán lớp 9, đồng thời là giúp các bạn chuẩn bị tốt kiến thức cho kì thi HK 2 sắp tới. Mời các bạn tham khảo tài liệu trên

.......................................................................

Ngoài Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Bình Phước năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt