Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020

Đề kiểm tra học HK2 môn Toán lớp 9 có đáp án

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm 2020

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020 được VnDoc sưu tầm và đăng tải. Nội dung đề thi gồm có 5 bài toán tự luận, đề thi gồm 01 trang. Với tổng thời gian học sinh làm bài thi là 120 phút, sẽ giúp ích cho các bạn học sinh ôn tập thử sức với các đề thi khác nhau. Sau đây là nội dung đề thi mời các bạn tham khảo

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Tài liệu học tập lớp 9. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đáp án đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm 2020

Phần I. Trắc nghiệm

Câu 1	C	Câu 5	B
Câu 2	A	Câu 6	C
Câu 3	D	Câu 7	D
Câu 4	A	Câu 8	B

Phần II. Tự luận (8,0 điểm)

Câu 1. (1,5 điểm)

1) Ta có:

$VT = \sqrt{7+4\sqrt3} + \sqrt{7-4\sqrt3}$ $VT = \sqrt{7+4\sqrt3} + \sqrt{7-4\sqrt3}$

$= \sqrt{4+2.2\sqrt3+3 }+ \sqrt{4-2.2\sqrt3+3}$ $= \sqrt{4+2.2\sqrt3+3 }+ \sqrt{4-2.2\sqrt3+3}$

$= \sqrt{(2+\sqrt3)^2} + \sqrt{(2-\sqrt3)^2}$ $= \sqrt{(2+\sqrt3)^2} + \sqrt{(2-\sqrt3)^2}$

$= (2+\sqrt3) + (2-\sqrt3) = 4 (đpcm).$ $= (2+\sqrt3) + (2-\sqrt3) = 4 (đpcm).$

2)

Với x> 0; x ≠ 1, ta có:

$Q= \dfrac{\sqrt x -1}{x^2-x}: \left( \dfrac{1}{\sqrt x}- \dfrac{1}{\sqrt x+1} \right)$ $Q= \dfrac{\sqrt x -1}{x^2-x}: \left( \dfrac{1}{\sqrt x}- \dfrac{1}{\sqrt x+1} \right)$

$= \dfrac{\sqrt x -1}{x(\sqrt x-1)(\sqrt x+1)}: \dfrac{1}{\sqrt x(\sqrt x+1)}$ $= \dfrac{\sqrt x -1}{x(\sqrt x-1)(\sqrt x+1)}: \dfrac{1}{\sqrt x(\sqrt x+1)}$

$= \dfrac{1}{x(\sqrt x+1)}.{\sqrt x(\sqrt x+1)} = \dfrac{1}{\sqrt x}.$ $= \dfrac{1}{x(\sqrt x+1)}.{\sqrt x(\sqrt x+1)} = \dfrac{1}{\sqrt x}.$

Câu 2. (1,5 điểm)

Cho phương trình $x^2-3x+m=0 (1)$ với m là tham số, .

1)

Thay m = 1 vào (1), ta có:

$(1) ⇔ x^2-3x+1=0$

$⇔ \left[ \matrix{ {x} = \dfrac{3+\sqrt 5}{2} \hfill \cr {x} = \dfrac{3-\sqrt 5}{2} \hfill \cr} \right.$ $⇔ \left[ \matrix{ {x} = \dfrac{3+\sqrt 5}{2} \hfill \cr {x} = \dfrac{3-\sqrt 5}{2} \hfill \cr} \right.$

2) Để phương trình (1) có hai nghiệm phân biệt khi và chỉ khi:

$\Delta = 3^2 - 4m = 9 - 4m > 0 ⇔ m < \dfrac{9}{4}$ $\Delta = 3^2 - 4m = 9 - 4m > 0 ⇔ m < \dfrac{9}{4}$

Áp dụng hệ thức Vi-ét vào phương trình (1), ta có:

$\left\{ \matrix{ x_1+x_2 = 3 \hfill \cr x_1x_2 = m \hfill \cr} \right.$ $\left\{ \matrix{ x_1+x_2 = 3 \hfill \cr x_1x_2 = m \hfill \cr} \right.$

Ta có:

$x_1^2+x_2^2 = 2020$

$⇔ (x_1+x_2)^2 -2 x_1x_2= 2020$

$⇔ 3^2 -2 m= 2020$

$⇔ m = \dfrac{-2011}{2}$ $⇔ m = \dfrac{-2011}{2}$(thoả mãn đk)

⇒ Kết luận.....

Câu 3. (1,0 điểm) Giải hệ phương trình:

$\left\{ \matrix{ 2\sqrt{x+1} + \dfrac{3}{y-1} = 5 \hfill \cr 3\sqrt{x+1} + \dfrac{2}{y-1} = 5 \hfill \cr} \right.$ $\left\{ \matrix{ 2\sqrt{x+1} + \dfrac{3}{y-1} = 5 \hfill \cr 3\sqrt{x+1} + \dfrac{2}{y-1} = 5 \hfill \cr} \right.$

$ĐKXĐ: x \geq -1; y≠1$ $ĐKXĐ: x \geq -1; y≠1$

$⇔ \left\{ \matrix{ \sqrt{x+1} =1 \hfill \cr \dfrac{1}{y-1} = 1 \hfill \cr} \right.$ $⇔ \left\{ \matrix{ \sqrt{x+1} =1 \hfill \cr \dfrac{1}{y-1} = 1 \hfill \cr} \right.$

$⇔ \left\{ \matrix{x = 0 \hfill \cr y = 2 \hfill \cr} \right.$ $⇔ \left\{ \matrix{x = 0 \hfill \cr y = 2 \hfill \cr} \right.$ (thoả mãn đkxđ)

⇒ Kết luận.....

Câu 4. (3,0 điểm)

Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O). Gọi H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác ABC.

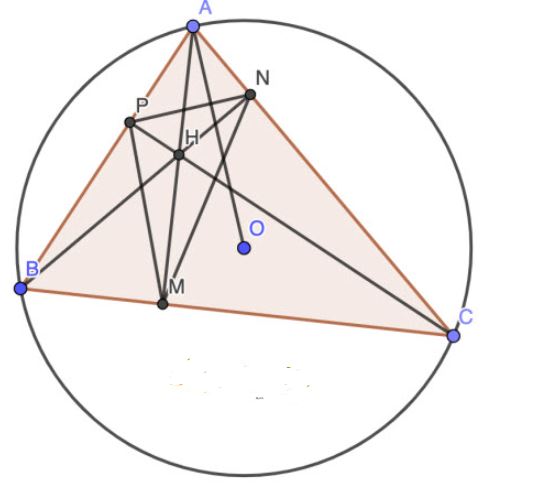
Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020

1)

Vì H là trực tâm và M, N, P lần lượt là chân đường cao kẻ từ các đỉnh A, B, C của tam giác $ABC ⇒ ∠APH = ∠ANH = 90° ⇒ P$ và N cùng thuộc đường tròn đường kính AH, hay tứ giác APHN là tứ giác nội tiếp (đpcm).

Tương tự ta có $∠BPC = ∠BNC = 90° ⇒ P$ và N cùng thuộc đường tròn đường kính BC, hay tứ giác BPNC là tứ giác nội tiếp (đpcm).

2)

Vì tứ giác APHN là tứ giác nội tiếp$⇒ ∠HPN = ∠HAN$ (Góc nội tiếp (ABHN) cùng chắn cung HN)

Tương tự ý trên, ta chứng minh được các tứ giác BPHM và CNHM nội tiếp.

$⇒ ∠HPM = ∠HBM = 90° - ∠BHM = 90° - ∠AHN = ∠HAN = ∠HPN$

Hay PH là phân giác trong của góc NPM.

Chứng minh tương tự ta có: $∠PNH = ∠HNM ⇒ PH$ là phân giác trong của góc PNM.

Hay H là giao của ba đường phân giác trong của tam giác MNP, hay H là tâm đường tròn nội tiếp tam giác MNP (đpcm).

3) Chứng minh đường thẳng OA vuông góc với đường thẳng NP.

Vì tứ giác BPNC nội tiếp (cmt) $⇒ ∠ACB = ∠NCB = 180° - ∠NPB = ∠APN (1)$

Ta lại có: $∠PAO = 90° - ∠AOB/2 = 90° - ∠ACB (2)$

Từ (1) và (2) ta có: $∠PAO + ∠APN = 90° ⇒ AO ⊥ PN (đpcm).$

Câu 5. (1,0 điểm)

1) Giải phương trình $\sqrt{x-2} + \sqrt{10-x}=(x-6)^2 (x - 2)(10 - x) +4\ (1)$ $\sqrt{x-2} + \sqrt{10-x}=(x-6)^2 (x - 2)(10 - x) +4\ (1)$

$ĐKXĐ: 2 \leq x \leq 10$ $ĐKXĐ: 2 \leq x \leq 10$

Ta có 2 $\leq x \leq 10$ $\leq x \leq 10$

$\Rightarrow (x-6)^2 (x - 2)(10 - x) \geq 0$ $\Rightarrow (x-6)^2 (x - 2)(10 - x) \geq 0$

$\Rightarrow VP(1) = (x-6)^2 (x - 2)(10 - x) + 4 \geq 4 (*)$ $\Rightarrow VP(1) = (x-6)^2 (x - 2)(10 - x) + 4 \geq 4 (*)$

Áp dụng BĐT Bunhya Cốp-xki, ta có:

$VT (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq \sqrt{(1+1)(x-2+10-x)} = 4 (**)$ $VT (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq \sqrt{(1+1)(x-2+10-x)} = 4 (**)$

Từ (*) và (**) ta có:

$VT\ (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq 4 \leq (x-6)^2 (x - 2)(10 - x) + 4 = VP\ (1)$ $VT\ (1) = 1.\sqrt{x-2} + 1.\sqrt{10-x} \leq 4 \leq (x-6)^2 (x - 2)(10 - x) + 4 = VP\ (1)$

Vậy (1) xảy ra $\Leftrightarrow VT(1) = VP(1) = 4$ $\Leftrightarrow VT(1) = VP(1) = 4$

$\Leftrightarrow \left\{ \matrix{ (x-6)^2 (x - 2)(10 - x) = 0 \hfill \cr \sqrt{x-2} = \sqrt{10-x} \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ (x-6)^2 (x - 2)(10 - x) = 0 \hfill \cr \sqrt{x-2} = \sqrt{10-x} \hfill \cr} \right.$

$\Leftrightarrow x=6$ $\Leftrightarrow x=6$

Kết luận ......

2) Ta có:

$a\left(a - \dfrac{2021}{3} \right) + b\left(b - \dfrac{2021}{3} \right) + c\left(c - \dfrac{2021}{3} \right) + \dfrac{2020}{3} \leq 0$ $a\left(a - \dfrac{2021}{3} \right) + b\left(b - \dfrac{2021}{3} \right) + c\left(c - \dfrac{2021}{3} \right) + \dfrac{2020}{3} \leq 0$

$\Leftrightarrow a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$ $\Leftrightarrow a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$

Áp dụng BĐT quen thuộc:

$a^2+b^2+c^2 \geq \dfrac{1}{3}(a+b+c)^2$ $a^2+b^2+c^2 \geq \dfrac{1}{3}(a+b+c)^2$

$\Leftrightarrow \dfrac{1}{3} (a+b+c)^2 - \dfrac{2021}{3}$ $\Leftrightarrow \dfrac{1}{3} (a+b+c)^2 - \dfrac{2021}{3}$

$(a+b+c)+ \dfrac{2020}{3} \leq a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$ $(a+b+c)+ \dfrac{2020}{3} \leq a^2+b^2+c^2 - \dfrac{2021}{3} (a+b+c)+ \dfrac{2020}{3} \leq 0$

$\Leftrightarrow (a+b+c)^2 -{2021}(a+b+c)+ {2020} \leq 0$ $\Leftrightarrow (a+b+c)^2 -{2021}(a+b+c)+ {2020} \leq 0$

$\Leftrightarrow (a+b+c - 1)(a+b+c-2020) \leq 0$ $\Leftrightarrow (a+b+c - 1)(a+b+c-2020) \leq 0$

$\Leftrightarrow 1 \leq S \leq 2020$ $\Leftrightarrow 1 \leq S \leq 2020$

Vậy ${min} _S = 1 \Leftrightarrow a=b=c= \dfrac{1}{3}$ ${min} _S = 1 \Leftrightarrow a=b=c= \dfrac{1}{3}$

${max} _S = 2020 \Leftrightarrow a=b=c= \dfrac{2020}{3}.$ ${max} _S = 2020 \Leftrightarrow a=b=c= \dfrac{2020}{3}.$

Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020 được VnDoc chia sẻ trên đây. Đây là đề cương hay giúp các bạn học sinh củng cố kiến thức Toán lớp 9, đồng thời là giúp các bạn chuẩn bị tốt kiến thức cho kì thi HK 2 sắp tới. Mời các bạn tham khảo tài liệu trên

.......................................................................

Ngoài Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Nam Định năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

2

11.316

Bài trước

Bài sau