Đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 trường THPT Thuận Thành 1, Bắc Ninh năm học 2015 - 2016
Đề thi khảo sát chất lượng đầu năm môn Toán lớp 12
Đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 trường THPT Thuận Thành 1, Bắc Ninh năm học 2015 - 2016 là đề kiểm tra đầu năm nhằm đánh giá chất lượng học sinh sau dịp hè. Đề thi môn Toán có đáp án đi kèm, sẽ giúp các em ôn tập và củng cố kiến thức hiệu quả. Mời các em cùng tham khảo.
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 12 LẦN 1
NĂM HỌC 2015-2016
Môn: TOÁN THPT
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu 1 (2,0 điểm)
a) Viết phương trình tiếp tuyến của đồ thị hàm số y = x3 + x2 - 2x +1 tại điểm có hoành độ x = 1.
b) Tìm m để phương trình: ![]() có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
Câu 2 (1,0 điểm).
a) Giải phương trình: 2cosx + sinx = 1 + sin2x.
b) Cho cosα = 1/3, -π/2 < α < 0. Tính ![]() .
.
Câu 3 (1,0 điểm). Tìm giá trị nhỏ nhất của hàm số: 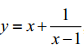 .
.
Câu 4 (1,0 điểm).
a) Tìm số hạng không chứa x trong khai triển Niu-tơn của biểu thức ![]() , với x ≠ 0.
, với x ≠ 0.
b) Từ các chữ số 0; 1; 2; 3; 4 lập được bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau. Lấy ngẫu nhiên một số trong các số lập được, tính xác suất để lấy được số chẵn.
Câu 5 (1,5 điểm). Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC), SA = a√6, AB = AC = a√3, góc BAC bằng 1200; lấy điểm M trên cạnh BC sao cho MC = 2MB.
a) Tính góc giữa đường thẳng SB với mặt phẳng (ABC).
b) Tính theo a thể tích của khối chóp S.ABC và khoảng cách giữa hai đường thẳng SM và AC.
Câu 6 (1,5 điểm)
a) Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x - y + 2 = 0 và A(1;1). Viết phương trình đường tròn tâm A và tiếp xúc với d.
b) Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác nhọn ABC. Đường thẳng chứa đường trung tuyến kẻ từ đỉnh A và đường thẳng BC lần lượt có phương trình là 3x + 5y - 8 = 0, x - y - 4 = 0. Đường thẳng qua A vuông góc với đường thẳng BC cắt đường tròn ngoại tiếp tam giác ABC tại điểm thứ hai là D(-4; -2). Viết phương trình các đường thẳng AB, AC; biết rằng hoành độ của điểm B không lớn hơn 3.
Câu 7 (1,0 điểm). Giải hệ phương trình: 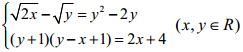
Câu 8 (1,0 điểm). Cho a, b, c > 0 thỏa mãn: a2 + b2 + c(a + b) + 4c2 = 4. Tìm giá trị lớn nhất của biểu thức: 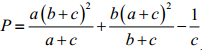
Đáp án đề thi khảo sát chất lượng đầu năm môn Toán lớp 12








