Đề thi thử THPT Quốc gia môn Toán lần 3 năm 2015 trường THPT Hai Bà Trưng, Thừa Thiên Huế
Đề thi thử THPT Quốc gia môn Toán
Kỳ thi THPT Quốc gia năm 2015 đang tới gần. Nhằm giúp các bạn thí sinh gấp rút luyện thi, thử sức trước các kỳ thi quan trọng, VnDoc.com xin giới thiệu đề thi thử THPT Quốc gia môn Toán lần 3 năm 2015 trường THPT Hai Bà Trưng, Thừa Thiên Huế có đáp án chi tiết. Mời các bạn cùng tham khảo.
Đề thi thử THPT môn Toán lần 2 năm 2015 trường THPT Hai Bà Trưng, Thừa Thiên Huế
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Triệu Sơn 3, Thanh Hóa
| SỞ GD&ĐT THỪA THIÊN HUẾ TRƯỜNG THPT HAI BÀ TRƯNG (ĐỀ CHÍNH THỨC) | THI THỬ KỲ THI THPT NĂM HỌC 2014-2015 Lần thứ ba - Môn: Toán Thời gian làm bài: 180 phút (không kể thời gian phát đề) |
Họ và tên thí sinh: ........................................................ Số báo danh: ..........
| Câu 1 (2,0 điểm): Cho hàm số | (1) |
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1) khi m = 1.
b. Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp điểm có tung độ y = 3.
c. Tìm các giá trị m ≠ 3 để hàm số (1) đồng biến trên các khoảng xác định của nó.
Câu 2 (1,0 điểm):
a. Cho sin(π + α) = -1/2 với π/2 < α < π. Tính tan(7π/2 - α).
b. Giải bất phương trình 8.3√x-x + 9√x-x+1 ≥ 1.
Câu 3 (1,0 điểm): Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng x = ln 3, x = ln8.
, trục hoành và hai đường thẳng x = ln 3, x = ln8.
Câu 4 (1,0 điểm): Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc BAD = 600 và AC' = 2a. Gọi O là giao điểm của AC và BD, E là giao điểm của A'C và OC'. Tính thể tích khối lăng trụ ABCD.A'B'C'D' và khoảng cách từ điểm A đến mặt phẳng (EBD).
Câu 5 (1,0 điểm): Trong mặt phẳng tọa độ Oxy, cho tam giác nhọn ABC, gọi E, F lần lượt là hình chiếu của các đỉnh B, C lên các cạnh AC, AB. Các đường thẳng BC và EF lần lượt có phương trình là BC: x - 4y - 12 = 0, EF: 8x + 49y - 6 = 0, trung điểm I của EF nằm trên đường thẳng Δ: x - 12y = 0. Tìm tọa độ các đỉnh của tam giác ABC biết BC = 2√17 và đỉnh B có hoành độ âm.
Câu 6 (1,0 điểm): Trong không gian Oxyz cho ba điểm A B (-1; -2;0), B(-5; -3;1), C(-2; -3; 4) và đường thẳng ![]()
a. Chứng minh tam giác ABC đều. Tính diện tích tam giác ABC.
b. Tìm tọa độ điểm D thuộc đường thẳng Δ sao cho thể tích tứ diện D.ABC bằng 3.
Câu 7 (1,0 điểm):
a. Giải phương trình: ![]()
b. Từ tập E = {1;2;3;4;5}, lập các số tự nhiên có ba chữ số. Lấy ngẫu nhiên hai số trong các số vừa lập. Tính xác suất để trong hai số được lấy ra có ít nhất một số có đúng hai chữ số phân biệt.
Câu 8 (1,0 điểm): Tìm số phức z biết (z + 3 - i)2 - 6(z + 3 - i) + 13 = 0.
Câu 9 (1,0 điểm): Cho a, b, c ≥ 1 là các số thực thỏa mãn a + b + c = 6. Tìm giá trị lớn nhất của P = (a2 + 2)(b2 + 2)(c2 + 2).
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1 (2,0 điểm)
a. 1,0 điểm
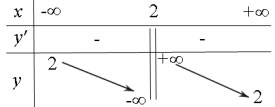
* Tập xác định: D= R \ {2}.
* Sự biến thiên:
Đạo hàm y' = -2/(x - 2)2 < 0, ∀x ∈ D. Hàm số nghịch biến trên mỗi khoảng (-∞; 2); (2; +∞)
Giới hạn:
![]() , nên đường thẳng y = 2 là tiệm cận ngang của đồ thị (C1).
, nên đường thẳng y = 2 là tiệm cận ngang của đồ thị (C1).
![]() , nên đường thẳng x = 2 là tiệm cận đứng của đồ thị (C1).
, nên đường thẳng x = 2 là tiệm cận đứng của đồ thị (C1).
Bảng biến thiên
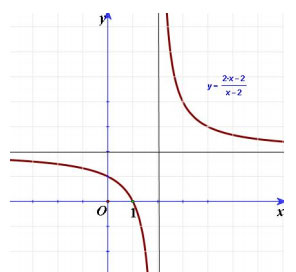
* Đồ thị: Đồ thị hàm số nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Điểm đặc biệt
![]()
b. 0,5 điểm
Ta có y = 3 → x = 4; y'(4) = -1/2
Phuowng trình tiếp tuyến của (C) tại điểm M(4; 3):
y -1/2(x - 4) + 3 ↔ y = -1/2x + 5
c. 0,5 điểm
Ta có y' = (-3 + m)/(x - 2)2, tập xác định D = R\{2}
Với m ≠ 3, hàm số đồng biến trên các khoảng (-∞; 2) và (2; +∞) khi và chỉ khi y' > 0, ∀x ≠ 2 ↔ m > 3.
Câu 2 (1,0 điểm)
a. 0,5 điểm
Ta có sin(π + α) = -1/2 → sinα = 1/3.
Do π/2 < α < π nên cosπ < 0 → cosα = -√(1 - 1/9) = -2√2/3.
tan(7π/2 - α) = tan(3π + π/2 - α) = tan(π/2 - α) = cotα = cosα/sinα = -2√2.
b. 0,5 điểm
Điều kiện: x ≥ 0
Bất phương trình tương đương với 8.3√x-x + 9.(3√x-x)2 - 1 ≥ 0
Đặt t = 3√x-x, t > 0, ta có 9t2 + 8t - 1 ≥ 0 ↔ t ≤ -1 (loại) hoặc t ≥ 1/9
Do vậy
3√x-x ≥ 1/9 ↔ √x - x ≥ -2 ↔ -x + √x + 2 ≥ 0 ↔ 0 ≤ √x ≤ 2 ↔ 0 ≤ x ≤ 4.
Vậy tập nghiệm của bất phương trình là T = [0; 4].






