Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Nguyễn Siêu, Hưng Yên

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Nguyễn Siêu, Hưng Yên có đáp án đi kèm, được VnDoc.com sưu tầm và đăng tải, giúp các bạn có nhiều đề để luyện tập, từ đó nâng cao kỹ năng làm bài. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Trung Giã, Hà Nội

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Marie Curie

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Hà Nội - Amsterdam

TRƯỜNG THPT NGUYỄN SIÊU (Đề gồm 9 câu 1 trang)

ĐỀ THI THỬ KỲ THI THPT QUỐC GIA ĐỢT I NĂM HỌC: 2015 - 2016 MÔN: TOÁN (Thời gian làm bài: 180 phút, không kể thời gian phát đề)

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x⁴ - 2x² - 3.

Câu 2 (1,0 điểm). Viết phương trình tiếp tuyến với đồ thị (C) của hàm số f(x) = x³ - 6x² + 9x + 1 tại điểm thuộc đồ thị (C) có hoành độ là nghiệm của phương trình 2f'(x) - xf"(x) - 6 = 0.

Câu 3 (1,5 điểm).

a) Giải phương trình sin2x - 2√3cos2x - 2cosx = 0.

b) Giải phương trình 9^√x - 4.3^√x + 3 = 0.

c) Chị Mai ra chợ mua 4 quả cam, 3 quả lê, 6 quả quýt, 1 quả bưởi và 2 quả thanh long. Chị Mai chọn 8 quả trong số các quả mua về để bày thành mâm ngũ quả ngày tết. Tính xác suất để mâm ngũ quả chị Mai bày có đủ các loại quả mà chị mua về trong đó có ít nhất 3 quả cam.

Câu 4 (1,0 điểm). Tính nguyên hàm

Câu 5 (1,0 điểm). Tìm hệ số của x⁴ trong khai triển nhị thức Newton của , biết rằng A³_n + C¹_n = 49 + 8C²_n

Câu 6 (1,5 điểm). Cho hình lăng trụ tam giác ABC.A'B'C' biết AB = a, AC = 2a và BAC = 60^o. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC, góc giữa AA' và mặt phẳng (ABC) bằng 60^o. Tính theo a:

a) Thể tích khối lăng trụ ABC.A'B'C'

b) Khoảng cách từ C' đến mặt phẳng (A'BC).

Câu 7 (1,0 điểm). Trong mặt phẳng Oxy, cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC, G là trọng tâm tam giác ABM, D(7; 2) là điểm nằm trên đoạn MC sao cho GA=GD, phương trình đường thẳng AG là 3x - y - 13 = 0. Xác định tọa độ các đỉnh của tam giác ABC biết đỉnh A và B có hoành độ nhỏ hơn 4.

Câu 8 (1,0 điểm). Giải hệ phương trình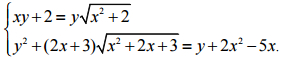

Câu 9 (1,0 điểm). Cho a, b, c là các số thực thỏa mãn 0 ≤ a ≤ b ≤ c.

Tìm giá trị nhỏ nhất của biểu thức

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán

Câu 1:

TXĐ : R

Sự biến thiên:

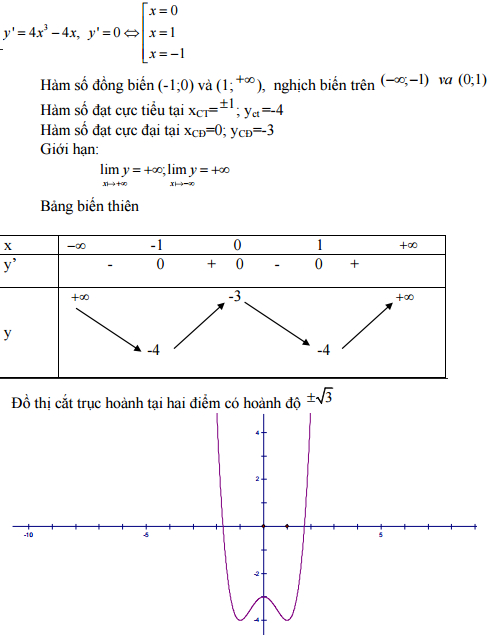
Câu 2:

Ta có f'(x)=3x² - 12x + 9; f''(x)=6x-12

2f'(x) - xf"(x) - 6 = 0 ↔ 2(3x² - 12x + 9) - x(6x - 12) - 6 = 0 ↔ x = 1

Tung độ là y = f(1) = 1³ - 61² + 9 + 1 = 5, hệ số góc k = f'(1) = 0

Phương trình tiếp tuyến là y = k(x - 1) + 5 = 5

(Còn tiếp)