Đề thi thử Toán vào lớp 10 phòng GD&ĐT Giao Thủy, Nam Định năm 2025 - 2026
Đề thi tuyển sinh lớp 10 môn Toán có đáp án
Lớp:
Ôn vào 10
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang
1
/2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN GIAO THỦY
ĐỀ THI THỬ TUYỂN SINH VÀO 10 THPT
NĂM HỌC 2025 – 2026
MÔN: Toán lớp 9 THCS
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Đề thi thử gồm có: 02 trang.
Phần I. Trắc nghiệm (2,0 điểm)
Hãy chọn chữ cái đứng trước phương án trả lời đúng và ghi chữ cái đó vào bài làm.
Câu 1. Tổng hai nghiệm của phương trình
2
2 6 3 0x x
bằng
A.
3.
B.
3.
C.
6.
D.
3
.
2
Câu 2. Hệ phương trình
2 0
3 2 8
x y
x y
có nghiệm
0 0
( ; y )x
. Khi đó
0 0
yx
bằng
A.
1.
B.
0.
C.
1.
D.
3.
Câu 3. Tất cả các giá trị của
x
để biểu thức
2025 2026P x
có nghĩa là
A.
2026.x
B.
2026.x
C.
2026.x
D.
2026.x
Câu 4
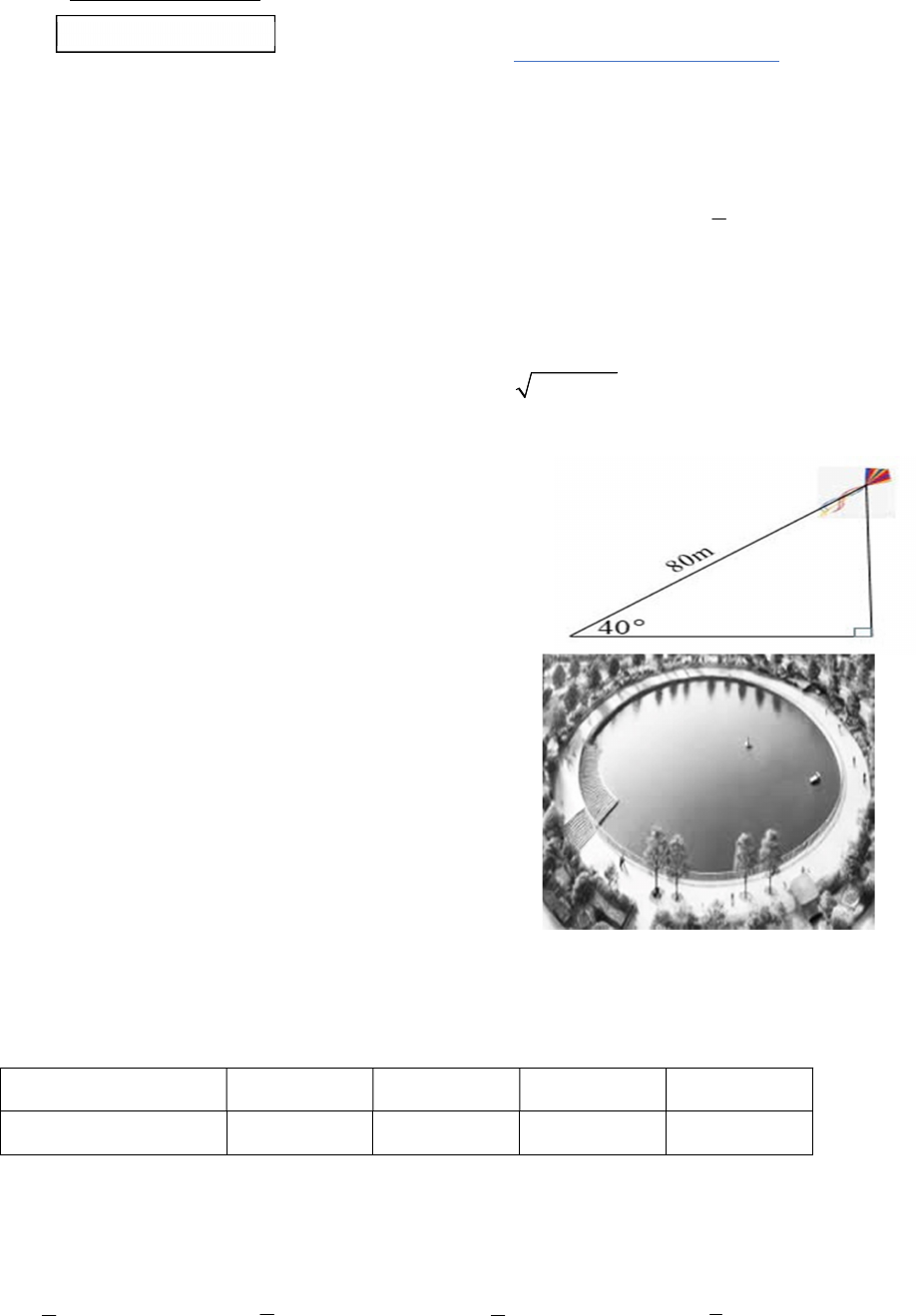
.
Một con diều đang bay với đầu dây buộc cố định
trên mặt đất. Sợi dây có độ dài
80 m
và tạo với mặt đất
một góc
40
(hình vẽ minh hoạ). Hỏi con diều đang bay
ở độ cao bao nhiêu
m
so với mặt đất (làm tròn đến chữ
số thập phân thứ nhất)?
A.
51, 4 .m
B.
61,3 .m
C.
67,1 .m
D.
95,3 .m
C
âu
5
.
Một hồ nước hình tròn, mặt hồ có đường kính
20 ,m
quanh hồ có một lối đi hình vành khăn rộng
2 .
m
Diện tích lối đi bằng (kết quả làm tròn đến hàng phần
trăm của
2
m
)
A.
2
128,23 .m
B.
2
138,23 .m
C.
2
12,57 .m
D.
2
314,16 .m
Câu 6. Diện tích xung quanh của hình nón có bán kính đáy
4 cm
và độ dài đường sinh
10 cm
là
A.
40 cm.
B.
2
400 cm .
C.
2
40 cm .
D.
2
40 cm .
Câu 7. Để tìm hiểu thói quen học tập của học sinh lớp 9A, cô giáo chủ nhiệm đã thực hiện khảo
sát và ghi nhận số giờ học bài mỗi ngày của học sinh lớp 9A như sau:
Thời gian học (giờ)
[0;1)
[1; 2)
[2;3)
[3; 4)
Tần số tương đối
25%
50%
20%
5%
Nếu lớp 9A có 40 học sinh thì bao nhiêu học sinh học bài từ 2 đến dưới 3 giờ mỗi ngày?
A.
12.
B.
10.
C.
9.
D.
8.
Câu 8. Bạn Nam gieo đồng thời hai đồng xu (có một mặt sấp và một mặt ngửa, cần đối, đồng
chất). Xác suất để “Hai đồng xu có đúng một đồng xu xuất hiện mặt sấp” là
A.
1
.
2
B.
1
.
4
C.
3
.
4
D.
1
.
3
Đ
Ề
CHÍNH TH
Ứ
C

Trang
2
/2
Phần II. Tự luận (8,0 điểm)
Bài 1 (1,5 điểm).
a) Tính giá trị của biểu thức
2
9 4 2.
2 1
A
b) Rút gọn biểu thức
5
9
3
1 3
x x
x x
B
x
x x
với
0; 1.x x
Bài 2 (1,0 điểm). Một hộp chứa
30
thẻ cùng loại, trên mỗi thẻ được đánh số từ
1
đến
30
. Các
thẻ khác nhau ghi số khác nhau. Rút ngẫu nhiên một thẻ trong hộp đó.
1) Xác định số phần tử không gian mẫu của phép thử.
2) Tính xác suất của biến cố “Số ghi trên thẻ rút được là một số chính phương”.
Bài 3 (1,5 điểm).
1. Nhà bác học Galileo Galilei
1564 1642
là người đầu tiên phát hiện ra quãng đường
chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Liên hệ
giữa quãng đường chuyển động
S
(mét) và thời gian chuyển động
t
(giây) được cho bởi hàm số
2
4, 9S t
. Trong một thí nghiệm Vật lí, người ta thả một vật nặng rơi tự do từ độ cao
122,5 m
xuống đất (coi sức cản của không khí không đáng kể).
a) Hỏi sau thời gian bao nhiêu giây vật nặng rơi tự do sẽ chạm đất?
b) Sau thời gian
3
giây vật nặng rơi tự do còn cách mặt đất bao nhiêu mét?
2. Biết phương trình
2
2 5 0x x
có hai nghiệm phân biệt
1 2
; .x x
Không giải phương
trình, hãy tính giá trị của biểu thức
2 2
1 2
.M x x
Bài 4 (1,0 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Tiền cước điện thoại
y
(nghìn đồng) là số tiền mà người sử dụng cần trả hằng tháng, số
tiền đó phụ thuộc vào thời gian gọi
x
(phút) của người đó trong tháng. Mối liên hệ giữa hai đại
lượng này là một hàm số bậc nhất
0y ax b a
. Hãy xác định hàm số trên trong trường
hợp mẹ bạn An trong tháng 1/2025 đã gọi
100
phút với số tiền cước là
40
nghìn đồng và trong
tháng 2/2025 đã gọi
40
phút với số tiền cước là
28
nghìn đồng.
Bài 5 (1,0 điểm).
Một chi tiết máy có dạng hình trụ với bán kính
đáy bằng chiều cao và bằng
17 cm
. Người ta
khoan rỗng ở giữa chi tiết máy đó một lỗ cũng có
dạng hình trụ có bán kính đáy và độ sâu bằng
6 cm
(như hình vẽ). Tính thể tích của phần chi tiết
máy còn lại sau khi khoan (kết quả làm tròn đến
chữ số thập phân thứ hai của đơn vị tính).
Bài 6 (2,0 điểm). Qua điểm
P
nằm ngoài đường tròn
( )O
kẻ hai tiếp tuyến
PC
và
PN
. Đường
thẳng qua
P
cắt đường tròn
( )O
tại hai điểm
A
và
( ) B PA PB
sao cho ba điểm
, ,A B C
nằm
cùng một phía đối với
PO
. Vẽ đường kính
CD
của đường tròn
( )O
. Gọi
M
là trung điểm của
.AB
a) Chứng minh tứ giác
PCMO
nội tiếp và
//PO ND
.
b) Gọi
E
là giao điểm của
PO
và
BD
. Tia
CE
cắt
( )O
tại điểm thứ hai là
K
. Chứng minh
. .CM OD OE AM
và ba điểm
, ,A O K
thẳng hàng.
--------------- HẾT ---------------
Họ tên học sinh:………………………..
Số báo danh:……………….…………....
Họ tên, chữ kí giám thị số 1:…………………………
Họ tên, chữ kí giám thị số 2:……………..….………
Trang 1/5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN GIAO THỦY
HƯỚNG DẪN CHẤM
ĐỀ THI THỬ TUYỂN SINH VÀO 10 THPT
NĂM HỌC 2025 – 2026
MÔN: Toán lớp 9 THCS
Phần I: Trắc nghiệm (2,0 điểm)
Câu 1 2 3 4 5 6 7 8
Đáp án B C D A B C D A
Phần II: Tự luận (8,0 điểm)
Bài Ý Nội dung Điểm
Bài 1
1,5đ
Bài 1 (1,5 điểm).
a) Tính giá trị của biểu thức
2
9 4 2.
2 1
A
b) Rút gọn biểu thức
5
9
3
1 3
x x
x x
B
x
x x
với
0; 1.
x x
2
2
) 9 4 2
2 1
2( 2 1)
(2 2) 4 2 1
( 2 1)( 2 1)
a A
0,25
2
2( 2 1)
2 2 1
2 1
0,25
2( 2 1) 2 2 1
=2( 2 1) (2 2 1)
1
0,25
b) Với
0; 1,
x x
ta có:
5 1
9
3
1 3
5 9
=
3 3
x x
x x
B
x
x x
x x x
x x
0,25
5 9
=
3
6 9
=
3
x x x
x
x x
x
0,25
2
3
=
3
3
x
x
x
Vậy
3
B x
với
0; 1.
x x
0,25
Đề thi thử tuyển sinh vào lớp 10 môn Toán phòng GD&ĐT Giao Thủy, Nam Định năm 2025 - 2026
Mời các bạn tham khảo Đề thi thử Toán vào lớp 10 phòng GD&ĐT Giao Thủy, Nam Định năm 2025 - 2026 . Tài liệu với cấu trúc trắc nghiệm và tự luận, thời gian làm bài 120 phút. Đề thi có đáp án đi kèm cho các em so sánh đối chiếu sau khi làm xong. Mời các em thử sức làm bài.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.



