Phân dạng đề thi đại học môn Toán từ năm 2002 đến năm 2015
Phân dạng đề thi đại học môn Toán từ năm 2002 đến năm 2015
Phân dạng đề thi đại học môn Toán từ năm 2002 đến năm 2015 là tài liệu do Hoàng Ngọc Thế biên soạn, tổng hợp đề thi đại học các năm, được phân chia theo từng chuyên đề riêng như: khảo sát hàm số, lượng giác, phương trình, hệ phương trình, bất phương trình, tích phân và ứng dụng, hình học tổng hợp trong không gian... Hi vọng tài liệu này giúp các bạn ôn thi đại học môn Toán hiệu quả. Mời các bạn cùng tham khảo.
Ôn thi Đại học môn Toán - Chuyên đề: Số phức
Lời nói đầu
Tài liệu nhỏ này giới thiệu Đề thi ĐH môn toán từ năm 2002 (năm đầu tiên toàn quốc thi đề chung) đến năm 2015. Các đề thi được phân dạng và sắp xếp theo các chủ đề lớn:
- Khảo sát hàm số
- Lượng giác
- Phương trình, hệ phương trình, bất phương trình
- Tích phân và ứng dụng
- Hình học tổng hợp trong không gian
- Bất đẳng thức
- Phương pháp tọa độ trong không gian
- Phương pháp tọa độ trong mặt phẳng
- Số phức
- Tổ hợp - xác suất
Ở mỗi chủ đề, đề bài được sắp xếp theo năm thi và có đáp án hoặc hướng dẫn đi kèm giúp bạn đọc dễ theo dõi và kiểm tra kết quả của mình. Bạn đọc nên tự làm các đề thi sau đó so sánh với đáp án. Để làm được các đề thi này, đòi hỏi bạn đọc cần có một quá trình ôn tập kiên trì và có hiệu quả.
Trong quá trình tổng hợp vội vàng, hẳn là sẽ có nhiều thiếu sót. Rất mong nhận được sự đóng góp của các bạn.
1. Khảo sát hàm số
1. (A-2002) Cho hàm số
y = −x3 + 3mx2 + 3(1 − m2)x + m3 - m2 (1)
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 1.
b) Tìm k để phương trình: −x3 + 3x2 + k3 - 3k2 = 0 có 3 nghiệm phân biệt.
c) Viết phương trình đường thẳng qua 2 điểm cực trị của hàm số (1).
ĐA: b) − 1 < k < 3, k ≠ 0; k ≠ 2; c) y = 2x − m2 + m
2. (B-2002) Cho hàm số
y = mx4 + (m2 − 9)x2 + 10 (2)
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (2) khi m = 1.
b) Tìm m để hàm số (2) có ba cực trị.
ĐA: 0 < m < 3; m < -3
3. (D-2002) Cho hàm số
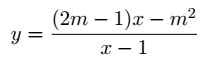 (3)
(3)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (3) khi m = −1.
b) Tính diện tích giới hạn bởi đồ thị (C) và 2 trục toạ độ.
c) Tìm điều kiện của tham số m đề đồ thị hàm số (3) tiếp xúc với đường thẳng y = x
ĐA: b) S = 4 ln4/3 - 1; c) m ≠ 1
4. (A-2003) Cho hàm số
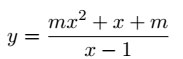 (4)
(4)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (4) khi m = −1.
b) Tìm điều kiện của tham số m để đồ thị hàm số (4) cắt Ox tại hai điểm phân biệt có hoành độ dương
ĐA: −1/2 < m < 0
5. (B-2003) Cho hàm số
y = x3 − 3x2 + m (5)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (5) khi m = 2.
b) Tìm điều kiện của tham số m để đồ thị hàm số (5) có hai điểm phân biệt đối xứng nhau qua gốc toạ độ.
ĐA: m > 0


