33 Thủ thuật Casio giải nhanh trắc nghiệm Toán 12
Thủ thuật Casio giải trắc nghiệm Toán 12
33 Thủ Thuật Casio Giải Nhanh Trắc Nghiệm Toán 12 vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Đây là một tài liệu tham khảo hay cho các bạn học sinh lớp 12 tự học và rèn luyện kĩ năng làm bài trắc nghiệm, ôn luyện cho kì thi THPT quốc gia và dành cho giáo viên tham khảo. Mời thầy cô cùng các bạn tham khảo chi tiết bài viết dưới đây để hiểu rõ hơn về thủ thuật Casio giải nhanh trắc nghiệm nhé.
Thi THPT Quốc gia môn Toán đã chuyển sang hình thức thi trắc nghiệm nhiều năm dự kiến trong kì thi THPT 2026 cũng không có nhiều thay đổi nhiều về hình thức thi nên việc rèn luyện kĩ năng sử dụng máy tính Casio thành thạo, giải nhanh các bài toán trắc nghiệm bằng máy tính Casio trong thời gian ngắn nhất là một lợi thế không nhỏ. Hiểu được sự lo lắng và cần thiết của vấn đề này, mời các bạn học sinh tham khảo nội dung của 33 Thủ thuật Casio giải nhanh trắc nghiệm Toán 12.
⇒ Bộ đề 9 môn thi thử THPT Quốc gia 2023
Trong tài liệu này tác giả xin giới thiệu 33 thủ thuật máy tính Casio để giải nhanh các dạng toán trắc nghiệm toán 12. Mỗi thủ thuật ứng với một chủ đề.Trong mỗi chủ đề được chia ra thành hai phần: các ví dụ đầu được thiết kế ở dạng đơn giản, học sinh chỉ được biết thủ thuật, bấm máy tính Casio là biết được đáp án nào là đáp án đúng A, B, C hay D mà không cần biết cách làm tự luận.
Phần hai là các ví dụ được thiết kế ở dạng nâng cao, dạng hạn chế sự lợi hại của máy tính casio, để làm được các bài toán này thì đòi hỏi sự phối hợp cao giữa tư duy tự luận và thủ thuật máy tính Casio.
Tài liệu gồm 5 phần trong chương trình Toán lớp 12, bao gồm:
- 8 thủ thuật tư duy Casio tìm nhanh GTLN, GTNN, tính đồng biến, nghịch biến, cực trị, tiếp tuyến, giới hạn, đạo hàm ... của hàm số, tìm nhanh tiệm cận, sự tương giao của đồ thị hàm số.
- 9 thủ thuật tư duy Casio tìm nhanh nghiệm, số nghiệm của phương trình, bất phương trình mũ - logarit, so sánh 2 đại lượng mũ - logarit, tính giá trị biểu thức mũ - logarit, Ôn thi Đại học môn Toán - Chuyên đề: Mũ và Logarit
- 6 thủ thuật tư duy Casio tìm nhanh nguyên hàm - tích phân, diện tích hình phẳng, thể tích khối tròn xoay, quãng đường vật chuyển động, giải các bài toán hạn chế máy tính Casio.
- 5 thủ thuật tư duy Casio giải nhanh bài toán vị trí tương đối, góc, khoảng cách, thể tích, hình chiếu vuông góc trong hình tọa độ không gian Oxyz.
- 5 thủ thuật tư duy Casio giải nhanh bài toán tìm số phức, mô-đun, số phức liên hợp, số phức nghịch đảo, acgument số phức, biểu diễn hình học số phức, quỹ tích điểm biểu diễn số phức, tìm min-max mô-đun số phức, giải phương trình số phức.
Hơn nữa, các ví dụ minh họa trong cuốn sách đều được cập nhật nhanh nhất theo cấu trúc của Bộ Giáo dục - Đào tạo. Các ví dụ được trích từ nguồn uy tín là đề thi thử Đại học của các trường chuyên trên cả nước vừa thi cách đây ít hôm như: Chuyên Khoa học Tự nhiên, chuyên Lam Sơn, chuyên Sư phạm, chuyên Vĩnh Phúc, chuyên Bắc Ninh, ...
Hy vọng tài liệu sẽ giúp các em học sinh rút ngắn thời gian hoàn thành đề thi và tránh sai sót trong quá trình tính toán, đồng thời giúp cộng đồng giáo viên có nguồn tài liệu tham khảo quý giá.
HÀM SỐ VÀ BÀI TOÁN LIÊN QUAN
Casio giải đề minh họa bộ giáo dục và đào tạo các năm
Câu 1. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
A. B.
C.
D.
Hướng dẫn giải
Ta có : là tiệm cận đứng

Đáp số chính xác là B
Chú ý: Ta thường nhầm lẫn đường thẳng với
là nghiệm của phương trình mẫu số bằng 0 luôn là tiệm cận đứng là không đúng!
(Xem chi tiết thủ thuật và bài tập tương tự tại bài: Casio tìm nhanh tiệm cận của đồ thị hàm sô)
Câu 2. Đồ thị hàm số và đồ thị hàm số
có tất cả bao nhiêu điểm chung?
A. 0 B. 4 C. 1 D. 2
Hướng dẫn giải
Số điểm chung cúa hai đô thị hàm số chính là số nghiệm của phương trình hoành độ giao điểm:
(1)
Máy tính Casio chí giải được phương trình bậc 3, không giải được phương trình bậc 4.
Vì vậy để máy tính có thể làm được ta tiến hành đặt ẩn phụ .
Khi đó (1)
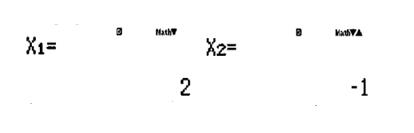
Với ,
Với (vô nghiêm)
Tóm lại có 2 nghiệm suy ra 2 giao điểm.
Câu 3. Cho hàm số . Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng -3. B. Cực tiểu của hàm số bằng 1.
C. Cực tiểu cúa hàm số bằng -6. D. Cực tiểu của hàm số bằng 2.
Hướng dẫn giải
Tính đạo hàm .
Ta chỉ quan tâm đến từ sỗ vì hoành độ điểm cực trị là nghiệm phương trình tử số .
Giải phương trình
Tiếp theo là xác định hoành độ điểm cực tiểu là bao nhiêu? Ta sử dụng tính năng tính đạo hàm
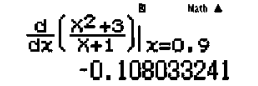
Ta thấy
Qua diểm
đạo hàm đối dấu từ âm ( - ) sang dương ( + )
Hàm số có điểm cực tiểu
Cực tiểu (giá trị cực tiểu) là: 2
Đáp số chính xác là
(Xem chi tiêt thủ thuật và bài tộp tương tụ tại bài: Casio giâi nhanh bài toán cục trị hàm số)
Câu 4. Một vật chuyển động theo quy luật với
(giây) là khoảng thời gian tírh từ lúc vật bắt đầu chuyển động và
(mét) là quāng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoàng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn rhất cúa vật đạt được bằng bao nhiêu (đơn vị
)?
A. 216 B. 30 C. 400 D. 54
Hướng dẫn giải
Gọi hàm số của vận tốc là .
Quãng đường vật đi được tính theo công thức
Hay ta hiểu
Bài toán lúc này trở thành tìm giá trị lớn nhất của hàm số trên miền thời gian từ 0 đến 10 giây.
Để làm việc này ta sử dụng tính năng lập bảng giá trị MODE 7 của Casio.
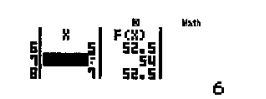
Quan sát bảng giá trị ta thấy giá trị lớn nhất xuất hiện là 54.
=> Đáp án chính xác là D.
(Xem chi tiết tại thủ thuật và bài tập tương tự tại bài: Casio giải nhanh bài toán thực tế cực trị)
Đạt điểm cao môn Toán là điều mà bất kì học sinh nào cũng mong muốn trong các kì thi, nhưng khối lượng kiến thức lớn, thi ở nhiều nội dung cũng như nhiều cách giải, tính toán nhiều dễ gặp sai lầm nên tìm kiếm tài liệu học tập, ôn thi luyện trắc nghiệm Toán các nội dung như Bài tập hàm số mũ và logarit, hệ thống kiến thức hình Oxyz, .....
Ngoài ra, không chỉ môn Toán mà các môn học khác cũng đóng vai trò quan trọng kém để các em có thể học tập toàn diện, không lệch tủ mời các em tham khảo thêm những tài liệu học tập chọn lọc khác như là:
- Tổng hợp 150 đoạn văn nghị luận xã hội 200 chữ
- Sơ đồ tư duy lý thuyết môn Sinh học lớp 12
- Công thức tính nhanh bài tập con lắc lò xo
- Bảng nhận biết các chất hữu cơ
- Cách tính nhanh đạo hàm
- Cách bấm máy tính đạo hàm
- 300 câu trắc nghiệm đạo hàm theo chủ đề có đáp án
Để tự tin bước vào thi THPT Quốc gia (Thi Đại học - Thi Tốt nghiệp THPT) VnDoc xin giới thiệu tới các bạn học sinh cùng tham khảo thêm một số tài liệu học tập các môn tại các mục Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học mà VnDoc tổng hợp và đăng tải để hỗ trợ các em vượt vũ môn thành công. Chúc các em đạt điểm cao trong các kì thi.







