Đề tham khảo tuyển sinh lớp 10 môn Toán sở GD&ĐT Vĩnh Phúc năm 2025 - 2026
Đề ôn thi vào lớp 10 môn Toán có đáp án
Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỪ NĂM HỌC 2025-2026
ĐỀ THI MÔN: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
Viết vào tờ giấy thi đáp án đúng mà em chọn (Ví dụ: Câu 1 nếu chọn A là đúng thì viết Câu 1: A).
Câu 1. Điều kiện xác định của biểu thức
2025x
là
A.
2025.x
B.
2025.x
C.
2025.x
D.
2025.x
Câu 2. Cặp số
; 3;2xy
là nghiệm của phương trình nào sau đây?
A.
3 9.xy
B.
2 3 12.xy
C.
5.xy
D.
2 1.xy
Câu 3. Hệ phương trình
3
31
xy
xy
có nghiệm là
A.
; 2;1 .xy
B.
; 0; 1 .xy
C.
; 3;0 .xy
D.
; 1;2 .xy
Câu 4. Tổng hai nghiệm của phương trình
2
2 3 1 0xx
là
A.
3
.
4
B.
3
.
2
C.
3
.
2
D.
3
.
4
Câu 5. Thống kê điểm kiểm tra giữa kì môn Toán của lớp 9A, ta thu được bảng số liệu sau:
Điểm
4
5
6
7
8
9
10
Số học sinh
2
3
4
8
13
8
7
Theo bảng số liệu trên, lớp 9A có bao nhiêu bạn đạt điểm 10?
A.
8.
B.
13.
C.
7.
D.
9.
Câu 6. Thống kê cân nặng của 25 quả bơ ta thu được bảng sau:
Cân nặng (g)
145;155
155;165
165;175
175;185
185;195
195;205
Số quả
2
4
7
8
3
1
Giá trị nào sau đây (tính bằng gam) đại diện cho nhóm
185;195 ?
A.
380.
B.
190.
C.
185.
D.
195.
Câu 7. Cho tam giác ABC vuông tại A. Khẳng định nào sau đây đúng?
A.
.sin .AB BC ABC
B.
.sin .AB BC ACB
C.
.cos .AB AC ACB
D.
.cos .AB BC ACB
Câu 8. Cho mặt cầu có bán kính bằng
1 cm.
Diện tích mặt cầu đó bằng
A.
2
4 .cm
B.
2
8 .cm
C.
2
16 .cm
D.
2
.cm
ĐỀ THAM KHẢO
Đề thi có 02 trang
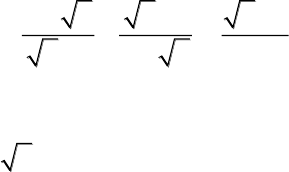
Trang 2
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 1 (1,0 điểm). Gieo một lần một con xúc xắc có dạng khối lập phương 6 mặt, cân đối và đồng
chất. Tính xác suất của biến cố: “Số chấm xuất hiện nhỏ hơn 3”.
Câu 2 (1,0 điểm). Cho biểu thức
11
:
1
x x x x
A
x
x x x
( 0, 1).xx
a) Rút gọn biểu thức
.A
b) Tìm giá trị nhỏ nhất của
2.B A x
Câu 3 (1,0 điểm). Thả một vật nặng hình cầu lăn từ trên đỉnh xuống chân một con dốc thẳng, dài
50m.
Quan hệ giữa quãng đường
y
(tính bằng mét) và thời gian
x
(tính bằng giây, kể từ khi bắt
đầu lăn) được thể hiện bởi công thức
2
1y a x
(với
a
là một hằng số nào đó). Biết rằng hết
4 giây đầu, vật lăn xuống được
8m.
Tính thời gian để vật đó lăn từ đỉnh xuống đến chân dốc.
Câu 4 (1,0 điểm). Bạn An và bạn Bình đến cửa hàng văn phòng phẩm mua bút chì và bút bi. Bạn
An mua 3 bút chì và 2 bút bi hết tổng số tiền 13500 (đồng), bạn Bình mua 2 bút chì và 4 bút bi
hết tổng số tiền 17000 (đồng). Biết rằng, giá mỗi loại bút chì, bút bi mà hai bạn mua là như nhau.
Hỏi giá mỗi bút chì và mỗi bút bi là bao nhiêu?
Câu 5 (3,0 điểm). Cho đường tròn
O
đường kính
2.AB R
Dây
MN
vuông góc với
AB
tại
,I
với
.IA IB
Trên đoạn
MI
lấy điểm
E
(
E
khác
M
và
I
). Tia
AE
cắt đường tròn
O
tại
điểm thứ hai là
.K
a) Chứng minh rằng tứ giác
IEKB
nội tiếp một đường tròn.
b) Chứng minh rằng tam giác AME đồng dạng với tam giác AKM và
2
. . 4 .AE AK BI BA R
c) Tính độ dài đoạn thẳng
OI
theo
R
khi chu vi tam giác
MIO
đạt giá trị lớn nhất.
Câu 6 (1,0 điểm). Cho ba số thực
,,abc
thỏa mãn các điều kiện
; 0a b c a b c
và
2 2 2
6.abc
Tìm giá trị nhỏ nhất của biểu thức
.P a b
—— Hết——
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:…………………………………….................; Số báo danh………………………....
Trang 1/4 - HDC
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
ĐỀ THAM KHẢO
HƯỚNG DẪN CHẤM TUYỂN SINH VÀO LỚP 10 THPT
TỪ NĂM HỌC 2025-2026
MÔN: TOÁN
(Hướng dẫn chấm có 04 trang)
Lưu ý:
- Hướng dẫn chỉ trình bày các bước cơ bản của một cách giải, nếu thí sinh có cách giải khác và
đúng vẫn cho điểm theo thang điểm của hướng dẫn chấm.
- Trong một bài, thí sinh giải đúng đến đâu cho điểm đến đó.
- Bài hình học, nếu không vẽ hình thì không cho điểm, nếu vẽ hình sai thì không cho điểm ứng với
phần vẽ hình sai.
- Trong các bài toán Giải phương trình, bất phương trình; Biến đổi, rút gọn biểu thức; Chứng
minh đẳng thức, bất đẳng thức ... thí sinh có thể sử dụng các dấu
,
hoặc không sử dụng,
nếu làm đúng, đều cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
I. PHẦN TRẮC NGHIỆM (2,0 điểm) Mỗi câu đúng cho 0,25 điểm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Câu 1 (1,0 điểm). Gieo một lần một con xúc xắc có dạng khối lập phương 6 mặt, cân đối và đồng
chất. Tính xác suất của biến cố: “Số chấm xuất hiện nhỏ hơn 3”.
Nội dung trình bày
Điểm
Con xúc xắc chỉ có thể xuất hiện các mặt có số chấm là: 1, 2, 3, 4, 5 hoặc 6
(hay không gian mẫu có 6 phần tử,
6n
).
0,50
Vì con xúc xắc cân đối và đồng chất nên khả năng xuất hiện các mặt là như nhau.
Gọi
E
là biến cố “Số chấm xuất hiện nhỏ hơn 3” ta suy ra
1; 2 ,E
hay
( ) 2.nE
0,25
Vậy xác suất cần tìm là
( ) 2 1
.
( ) 6 3
nE
PE
n
0,25
Câu 2 (1,0 điểm). Cho biểu thức
11
:
1
x x x x
A
x
x x x
(
0, 1xx
)
a) Rút gọn biểu thức
.A
Nội dung trình bày
Điểm
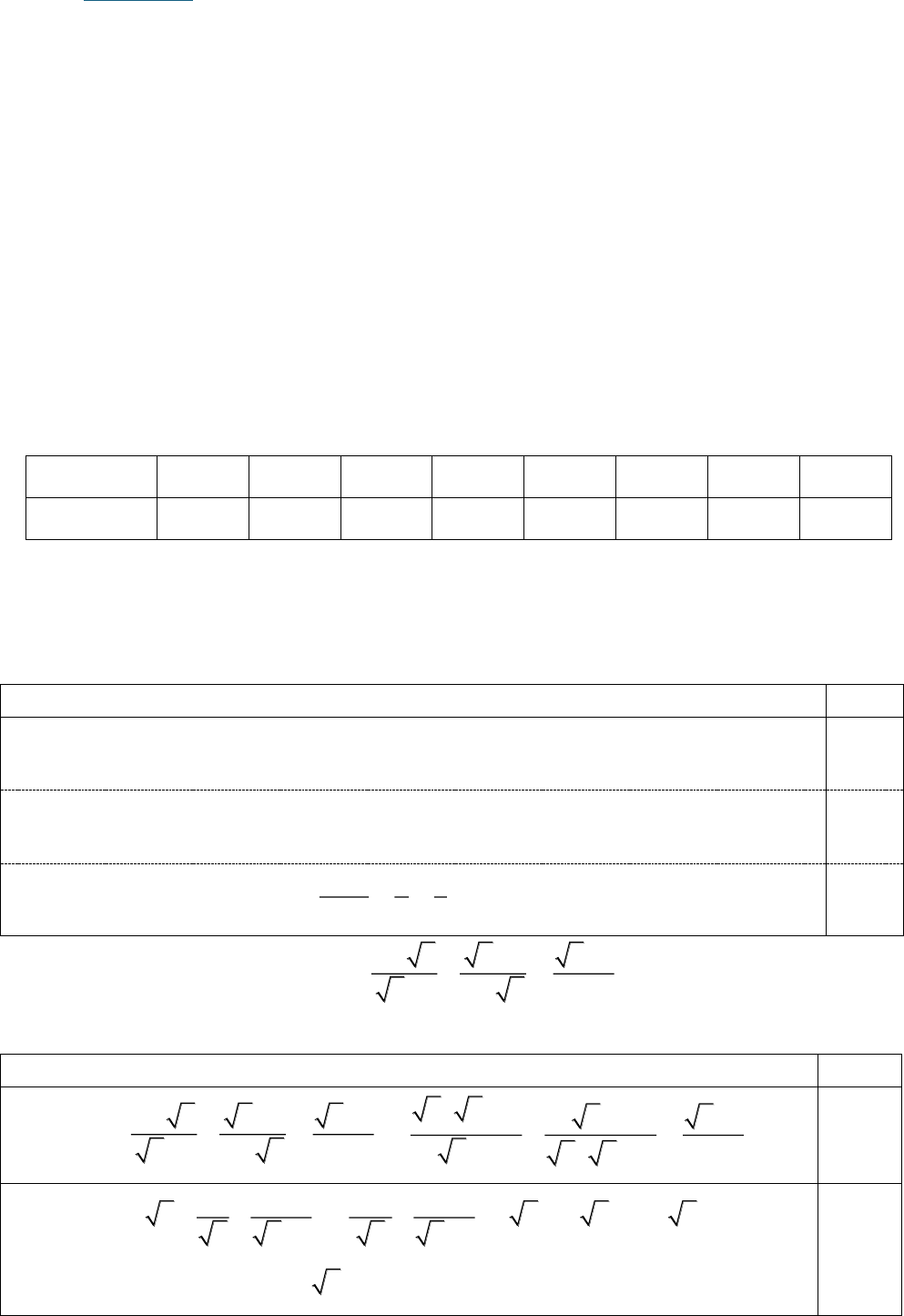
Ta có
11
:
1
x x x x
A
x
x x x
1
11
:
1
1
xx
xx
x
x
xx
0,25
11
. . 1 .
11
x x x
x x x x x
x x x x
Vậy với
0, 1xx
thì
.A x x
0,25
Câu
1
2
3
4
5
6
7
8
Đáp án
D
C
D
B
C
B
B
A
Đề minh họa thi vào 10 môn Toán 2025
VnDoc giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 Đề tham khảo tuyển sinh lớp 10 môn Toán sở GD&ĐT Vĩnh Phúc. Đề thi dưới hình thức tự luận, thời gian làm bài 120 phút, có đáp án và hướng dẫn chấm điểm.
Ngoài tài liệu trên, VnDoc còn gửi tới các bạn nhiều tài liệu tuyển sinh vào lớp 10 các môn để giúp các em ôn luyện, làm quen với nhiều đề thi khác nhau, chuẩn bị cho kì thi tuyển sinh vào lớp 10 năm học 2025 - 2026.
