Đề thi giải toán trên Máy tính cầm tay lớp 12 THPT tỉnh Quảng Ninh năm 2011 - 2012

Vndoc.com xin gửi đến các bạn: Đề thi giải toán trên Máy tính cầm tay lớp 12 THPT tỉnh Quảng Ninh năm 2011 - 2012.

Đề thi giải toán trên Máy tính:

ĐỀ THI MÔN: TOÁN (THPT)

BÀI 1 (5 điểm)

Cho hàm số . Tính gần đúng a và b biết đường thẳng y = a.x + b là tiếp tuyến của đồ thị hàm số tại điểm có hoành độ .

BÀI 2 (5 điểm)

Tìm các nghiệm thực gần đúng của hệ phương trình:

BÀI 3 (5 điểm)

Tìm nghiệm gần đúng (độ, phút, giây) của phương trình: 4sin²2x + 10(sinx + cosx) = 7

BÀI 4 (5 điểm)

Cho ∆ ABC có AB = 4; BC = 6; CA = 9. Đường tròn nội tiếp tam giác tiếp xúc với các cạnh AB; BC; CA lần lượt tại M; N; P. Tính gần đúng diện tích ∆ MNP.

BÀI 5 (5 điểm)

Cho biểu thức:

Trong khai triển và rút gọn của P(x), tìm số hạng không chứa x.

BÀI 6 (5 điểm)

Cho tứ diện ABCD có AB = CD = 5cm, AD = BC = 6cm, AC = BD = 7 cm. Xác định tâm, tính bán kính mặt cầu nội tiếp và ngoại tiếp tứ diện.

BÀI 7 (5 điểm)

Trong mặt phẳng Oxy, cho elip và đường thẳng d: y = 20x + 12.

1. Tìm gần đúng tọa độ giao điểm A, B của (E) và d.

2. Tìm gần đúng tọa độ điểm M thuộc (E) sao cho tam giác MAB có diện tích lớn nhất.

BÀI 8 (5 điểm)

Cho dãy số (u_n) xác định như sau: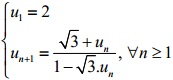

Đặt: Sn = u₁ + u₂ + ... + u_n với n = 1, 2, 3...

1) Tính S₃.

2) Tính gần đúng S₂₀₁₂ lấy đến 6 chữ số thập phân sau dấu phẩy.

BÀI 9 (5 điểm):

Một tấm đề can hình chữ nhật được cuộn tròn lạitheo chiều dài, được một khối trụ đường kính 50cm. Người ta trải ra 250 vòngđể cắt chữ và in tranh cổ động, khối còn lại là khối trụ có đường kính 45cm. Hỏi phần đã trải ra dài bao nhiêu mét (làm tròn đến hàng đơn vị)?

BÀI 10 (5 điểm)

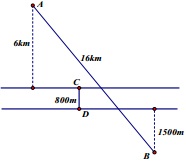
Hai thành phố A và B nằm ở hai phía khác nhau của một con sông thẳng, lòng sông rộng 800m; thành phố A ở bên phía phải cách bờ 6km và cách thành phố B theo đường chim bay 16km; thành phố B cách bờ trái 1500m. Người ta muốn xây một cây cầu CD vuông góc với bờ sông sao cho quãng đường bộ từ A đến B (độ dài đường gấp khúc ACDB) là ngắn nhất. Tính độ dài quãng đường đó.

ĐỀ THI MÔN: TOÁN (GIÁO DỤC THƯỜNG XUYÊN)

Bài 1 (6 điểm):

Với , hãy tính giá trị của biểu thức sau:

Bài 2 (5 điểm):

Tính gần đúng các nghiệm x thuộc (0; 2π) của phương trình:

Bài 3 (6 điểm):

Giải hệ phương trình (kết quả tính chính xác đến 9 chữ số thập phân):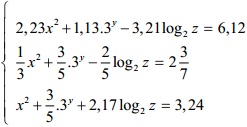

Bài 4 (5 điểm):

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với đáy, AB = 7dm, AD = 8dm, SA = 9dm. Tính gần đúng số đo góc tạo bởi mặt phẳng (SBD) với mặt đáy (ABCD) của hình chóp.

Bài 5 (5 điểm):

Gọi M, N là các giao điểm của đường tròn (C): x² + y² - 4x - 2y + 1 = 0 với đường thẳng (d): y - 2x + 1 = 0. Tính gần đúng độ dài MN.

Bài 6 (6 diểm):

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, cạnh bên SA vuông góc với đáy, mặt bên (SBC) tạo với đáy góc 45^o27'36'. Tính gần đúng diện tích xung quanh S của hình chóp S.ABCD biết AB = 2AD = 2DC = 6,912 cm.

Bài 7 (6 điểm):

Cho tam giác ABC biết: A(1; -1 ; -2) ; B(-1 ; 1 ; 2); C(2 ; -1 ; 1). Tính:

a) Độ dài đường cao BH của tam giác ABC.

b) Độ dài đường phân giác CK của tam giác ABC

Bài 8 (6 điểm):

Theo kết quả điều tra dân số, dân số trung bình nước Việt Nam qua một số mốc thời gian (đơn vị: 1.000 người) là:

a) Tính tỉ lệ % tăng dân số trung bình mỗi năm trong các giai đoạn 1976-1980, 1980-1990, 1990-2000, 2000-2010 (giả sử tỉ lệ % tăng dân số trung bình mỗi năm không đổi trong mỗi giai đoạn).

b) Nếu cứ duy trì tỉ lệ tăng dân số như ở giai đoạn 2000-2010 thì đến năm 2015 và 2020 dân số của Việt Nam là bao nhiêu?

Bài 9 (5 điểm):

Tính gần đúng giá trị nhỏ nhất và giá trị lớn nhất của hàm số: