Đề thi thử Quốc gia lần 1 năm 2015 môn Toán trường THPT Gia Viễn A, Ninh Bình

Đề thi thử Quốc gia lần 1 năm 2015 môn Toán trường THPT Gia Viễn A, Ninh Bình là đề luyện thi thử đại học môn Toán giúp các bạn tự kiểm tra trình độ bản thân, thử sức với các đề thi THPT Quốc gia môn Toán các trường, chuẩn bị tốt nhất cho kì thi THPT Quốc gia môn Toán sắp tới.

Đề thi thử Quốc gia lần 1 năm 2015 môn Vật Lý trường THPT Gia Viễn A, Ninh Bình

Đề thi thử Quốc gia lần 1 năm 2015 môn Sinh học trường THPT Gia Viễn A, Ninh Bình

Đề thi thử Quốc gia lần 1 năm 2015 môn Hóa học trường THPT Gia Viễn A, Ninh Bình

Đề thi thử THPT Quốc gia 2015 môn Tiếng Anh trường THPT Gia Viễn A, Ninh Bình (lần 1)

Đề thi thử THPT Quốc gia môn Toán

TRƯỜNG THPT GIA VIỄN A

ĐỀ THI THỬ THPT QUỐC GIA ĐỢT I NĂM HỌC 2014 – 2015; Môn: TOÁN Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Câu 1: (2,0 điểm). Cho hàm số y = 2x³ + 6x².

1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm m để đồ thị (C) cắt đường thẳng d: y = mx tại ba điểm phân biệt.

Câu 2: (1,0 điểm). Giải phương trình: sinx(sinx - 1)= cosx(1 - cosx).

Câu 3: (2,0 điểm). Tính các tích phân:

Câu 4: (1,0 điểm).

1. Giải phương trình: log_√2(4x) + √(log₂x + 2) = 10.
2. Tìm số hạng không chứa x trong khai triển nhị thức Niutơn của biểu thức: (2/√x + x²)¹⁵; (x > 0).

Câu 5: (1,0 điểm). Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1;1;-2), B(3;0;1), C(-1;2;3). Lập phương trình mặt phẳng (ABC). Lập phương trình mặt cầu (S) có bán kính R = 3, đi qua điểm A và có tâm thuộc trục Oy.

Câu 6: (1,0 điểm). Cho hình chóp S.ABCD có ABCD là hình chữ nhật, AC = 2a. Biết rằng ∆SAB đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD và tính độ dài đoạn thẳng MN với M, N lần lượt là trung điểm của SA và BC.

Câu 7: (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x² + y² - 2x + 4y + 1 = 0 và đường thẳng d: x + y – 3 = 0. Tìm trên d điểm M sao cho từ M có thể kẻ được hai tiếp tuyến đến đường tròn (C) là MA, MB (A, B là hai tiếp điểm) sao cho S_ΔMAB = 3S_ΔIAB, với I là tâm của đường tròn (C).

Câu 8: (1,0 điểm). Giải hệ phương trình:

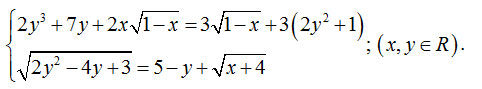
Đáp án đề thi thử Quốc gia môn Toán

Câu 1: (2,0 điểm)

1. (1,0 điểm)

TXĐ: D = R, y' = 6x² + 6x (0,25đ)

y' = 0 ↔ x = 0 hoặc x = -2. ta có y(0) = 0; y(-2) = 8

Giới hạn. (0,25đ)

Bảng biến thiên. Đồng biến, nghịch biến. Cực trị. (0,25đ)

Vẽ đồ thị. (0,25đ)

2/ (1,0 điểm)

Hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm của phương trình:

2x³ + 6x² = mx ↔ x(x² + 6x + m) = 0 ↔ x = 0 hoặc x² + 6x + m = 0 (*) (0,25đ)

Để hai đồ thị cắt nhau tại ba điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt khác 0. (0,25đ)

Khi đó: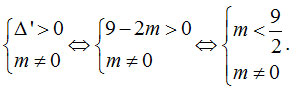

Câu 2: (1,0 điểm)

sinx(sinx - 1)= cosx(1 - cosx) ↔ sinx + cosx = 1 (0,25đ)

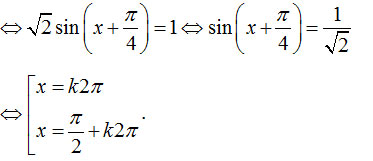
KL. (0,25đ)