Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Đào Duy Từ, Quảng Bình (Lần 2)

Đề thi thử THPT Quốc gia môn Toán năm 2016

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Đào Duy Từ, Quảng Bình (Lần 2) gồm 10 câu hỏi với thời gian làm bài 180 phút, có đáp án đi kèm. Đây là đề luyện tập hữu ích dành cho các bạn thí sinh chuẩn bị bước vào kì thi THPT Quốc gia, luyện thi Đại học, Cao đẳng 2016 sắp tới. Mời các bạn tham khảo!

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Thuận Thành 1, Bắc Ninh (Lần 1)

Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Đào Duy Từ

SỞ GD & ĐT QUẢNG BÌNH TRƯỜNG THPT ĐÀO DUY TỪ

ĐỀ THI THỬ THPT QUỐC GIA LẦN 2 NĂM 2016 Môn: TOÁN Thời gian làm bài: 180 phút, không kể thời gian giao đề

Câu 1 (1,0 điểm) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: .

Câu 2 (1,0 điểm) Viết phương trình tiếp tuyến của đồ thị hàm số: y = x³ - x² + 9x - 2 tại điểm có hoành độ x₀ thỏa mãn phương trình: y''(x₀) = -12.

Câu 3 (1,0 điểm)

a. Cho số phức thỏa mãn: . Tìm mô đun của số phức .

b. Giải phương trình log₃(9^x + 18) = x + 2.

Câu 4 (1,0 điểm) Tính tích phân: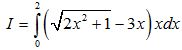

Câu 5 (1,0 điểm)

a. Cho góc α thỏa mãn và 3π/2 <α < 2π và cosα = 4/5. Tính giá trị của biểu thức: .

b. Trường THPT X tổ chức hội thao GDQP- AN. Trung đội 10A chọn một tiểu đội trong đó có 6 chiến sĩ nam và 5 chiến sĩ nữ tham gia các nội dung: hiểu biết chung về GDQP- AN, điều lệnh từng người không có súng, băng bó cứu thương và đội ngũ đơn vị. Tiểu đội trưởng chọn ngẫu nhiên 3 chiến sĩ tham gia nội dung băng bó cứu thương. Tính xác suất để 3 chiến sĩ được chọn có cả nam và nữ.

Câu 6 (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng (P): x + 2y − 2z + 3 = 0. Viết phương trình mặt phẳng (Q) đi qua gốc tọa độ O và vuông góc với d. Tìm tọa độ điểm M thuộc d sao cho khoảng cách từ M đến (P) bằng 3.

Câu 7 (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O với AB = 2a√3, BC = 2a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm H của đoạn OD. Góc hợp bởi SB với mặt đáy bằng 60^o. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AD và SC.

Câu 8 (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A thuộc đường thẳng d₁: 2 x - y + 2 = 0, đỉnh D thuộc đường thẳng d₂: x - y - 5 = 0. Gọi H là hình chiếu vuông góc của A trên BD. Điểm M(9/5; 2/5), N(9; 2) lần lượt là trung điểm của BH và CD. Xác định tọa độ các đỉnh của hình chữ nhật ABCD biết điểm D có tung độ dương.

Câu 9 (1,0 điểm) Giải hệ phương trình:

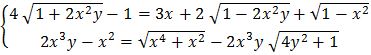
Câu 10 (1,0 điểm). Cho x, y, z là các số thực dương thỏa mãn y + z = x(y² + z²). Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi thử THPT Quốc gia môn Toán năm 2016