Đề thi tuyển sinh lớp 10 THPT chuyên Lam Sơn, Thanh Hóa - Môn Toán (2000 - 2010)

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT chuyên Lam Sơn, Thanh Hóa - Môn Toán (2000 - 2010).

Đề thi tuyển sinh lớp 10 môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA (Đề thi chính thức)

KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN LAM SƠN NĂM HỌC 2009-2010 KHÓA NGÀY 19/06/2009 Môn thi: TOÁN (Dành cho thí sinh thi vào lớp chuyên Toán) Thời gian làm bài : 150 phút (không kể thời gian giao đề)

Câu 1: (2,0 điểm)

1. Cho số x (x thuộc R, x > 0) thoả mãn điều kiện: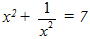

Tính giá trị các biểu thức: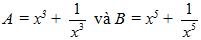

2. Giải hệ phương trình: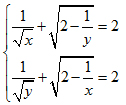

Câu 2: (2,0 điểm)

Cho phương trình: ax² + bx + c = 0 (a # 0) có hai nghiệm x₁, x₂ thoả mãn điều kiện: 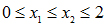. Tìm giá trị lớn nhất của biểu thức:

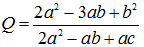
Câu 3: (2,0 điểm)

1. Giải phương trình: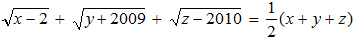

2. Tìm tất cả các số nguyên tố p để 4p² +1 và 6p² +1 cũng là số nguyên tố.

Câu 4: (3,0 điểm)

1. Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Một đường thẳng qua A, cắt cạnh BC tại M và cắt đường thẳng CD tại N. Gọi K là giao điểm của các đường thẳng EM và BN. Chứng minh rằng: CK vuông góc BN

2. Cho đường tròn (O) bán kính R = 1 và một điểm A sao cho 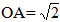. Vẽ các tiếp tuyến AB, AC với đường tròn (O) (B, C là các tiếp điểm). Một góc xOy có số đo bằng 45⁰ có cạnh Ox cắt đoạn thẳng AB tại D và cạnh Oy cắt đoạn thẳng AC tại E. Chứng minh rằng: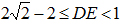

Câu 5: (1,0 điểm) Cho biểu thức P = a² + b² + c² + d² + ac + bd, trong đó ad - bc = 1
Chứng minh rằng: