Đề thi tuyển sinh lớp 10 THPT Chuyên trường ĐH Khoa học tự nhiên năm 2012 - 2013 môn Toán
Đề chuẩn bị cho kỳ thi vào cấp 3 sắp tới, Vndoc.com xin gửi đến các bạn: Đề thi tuyển sinh lớp 10 THPT Chuyên trường ĐH Khoa học tự nhiên năm 2012 - 2013 môn Toán.
Đề thi tuyển sinh môn Toán:
ĐẠI HỌC QUỐC GIA HÀ NỘI
|
KỲ THI TUYỂN SINH LỚP 10 HỆ CHUYÊN
|
Câu I.
1) Giải phương trình: ![]()
2) Giải hệ phương trình: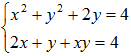
Câu II.
1) Tìm tất cả các cặp số nguyên (x; y) thỏa mãn đẳng thức: (x + y + 1)(xy + x + y) = 5 + 2(x + y)
2) Giả sử x, y là các số thực dương thỏa mãn điêu kiện ![]()
Tìm giá trị nhỏ nhất của biểu thức: ![]()
Câu III.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi M là một điểm trên cung nhỏ BC (M khác B, C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1) Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng N, P, D thẳng hàng
2) Đường tròn đường kính MP cắt MD tại Q khác M. Chứng minh rằng Q là tâm đườn tròn nội tiếp tam giác AQN.
Câu IV.
Giả sử a, b, c là các số thực dương thỏa mãn a ≤ b ≤ 3 ≤ c; c ≥ b + 1; a + b ≥ c
Tìm giá trị nhỏ nhất của biểu thức: ![]()


