Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - tỉnh Hà Tĩnh

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - tỉnh Hà Tĩnh.

Đề thi tuyển sinh lớp 10 môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ TĨNH ĐỀ THI CHÍNH THỨC

ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2012-2013 Môn thi: Toán Thời gian: 120 phút không kể thời gian giao đề Ngày thi 28 tháng 6 năm 2012

Câu 1 (2điểm)

a) Trục căn thức ở mẩu của biểu thức: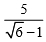

b) Giải hệ phương trình: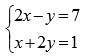

Câu 2 (2điểm)

Cho biểu thức:

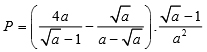với a >0 và A # 1

a) Rút gọn biểu thức P.

b) Với những giá trị nào của a thì P = 3.

Câu 3 (2điểm)

a) Trong mặt phẳng tọa độ Oxy, đường thẳng y = ax + b đi qua điểm M(–1 ; 2) và song song với đường thẳng y = 2x + 1. Tìm a và b.

b) Gọi x₁, x₂ là hai nghiệm của phương trình x² + 4x – m² – 5m = 0. Tìm các giá trị của m sao cho: |x₁ – x₂| = 4.

Câu 4 (3điểm)

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O. Hai đường cao AD, BE cắt nhau tại H (D thuộc BC, E thuộc AC).

a) Chứng minh tứ giác ABDE nội tiếp đường tròn.

b) Tia AO cắt đường tròn (O) tại K ( K khác A). Chứng minh tứ giác BHCK là hình bình hành.

c) Gọi F là giao điểm của tia CH với AB. Tìm giá trị nhỏ nhất của biểu thức: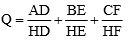

Câu 5 (1điểm) Tìm tất cả các giá trị của tham số m để phương trình sau vô nghiệm: x² – 4x – 2m|x – 2| – m + 6 = 0.