Ôn thi vào lớp 10 chuyên đề Hình học


Chuyên đề: Các bài toán hình học về đường tròn
Chuyên đề các bài toán hình học về đường tròn được VnDoc sưu tầm để giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh chuẩn bị một cách hiệu quả nhất cho Kì thi vào 10 sắp tới. Mời các bạn tham khảo.
- Kỹ năng giải toán bằng cách lập phương trình, hệ phương trình
- Tổng hợp các dạng Toán ôn thi vào 10 - Phần 1: Đại số
- Các dạng Toán cơ bản lớp 9 ôn thi vào lớp 10
- Một số bài Toán Thực tế thường gặp trong đề tuyển sinh vào 10
- 62 Bài tập Hình học lớp 9 ôn thi vào lớp 10
A. Nội dụng kiến thức cần biết của học kì I
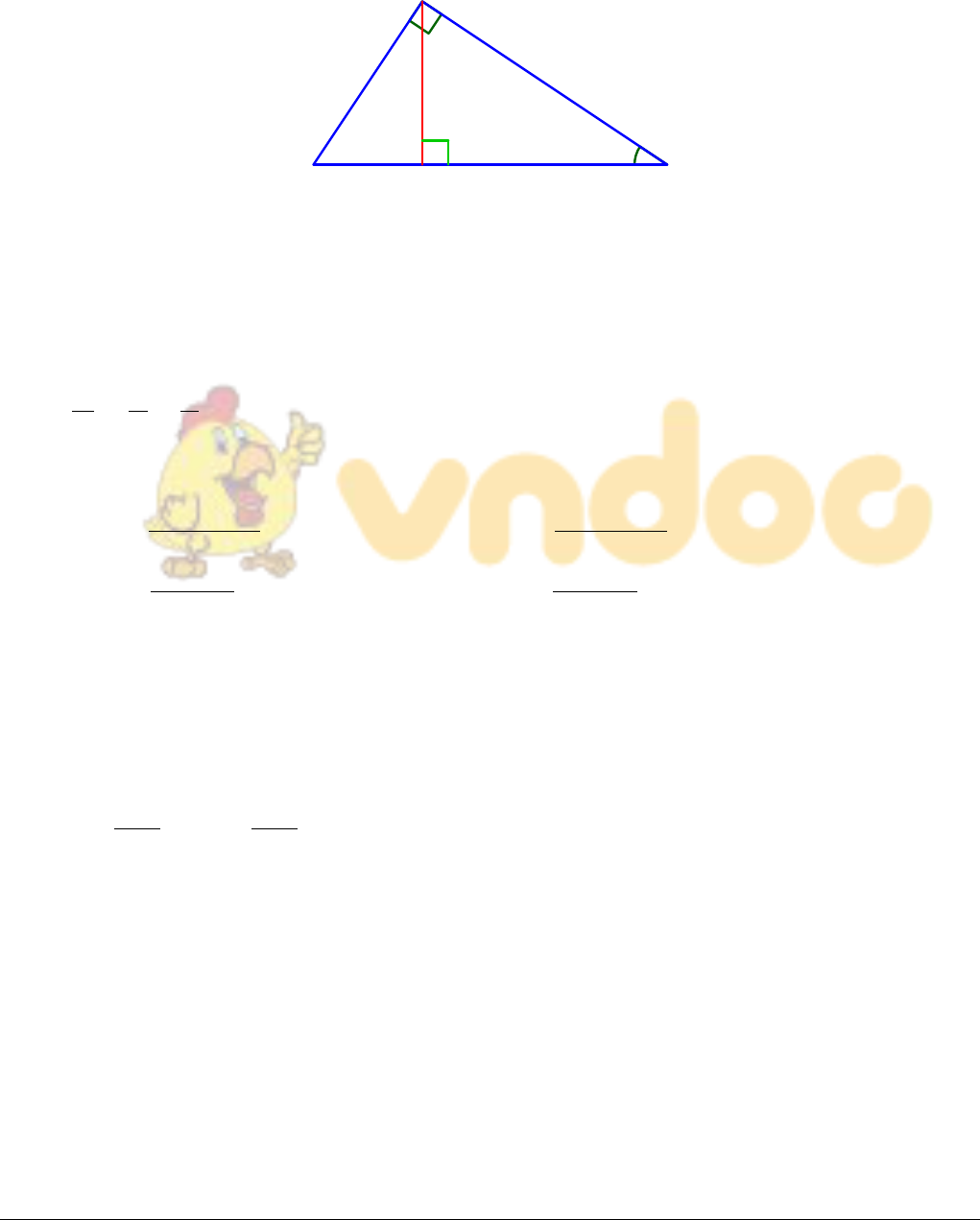
1. Hệ thức lượng trong tam giác vuông
2. Tỉ số lượng giác của góc nhọn
3. Một số tính chất của các tỉ số lượng giác
4. Các hệ thức về cạnh trong tam giác vuông
5. Cực trị hình học
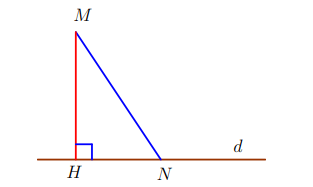
Vận dụng tính chất đường xiên và đường vuông góc MH ≤ MN.
Dấu ” = ” xảy ra khi N ≡ H.
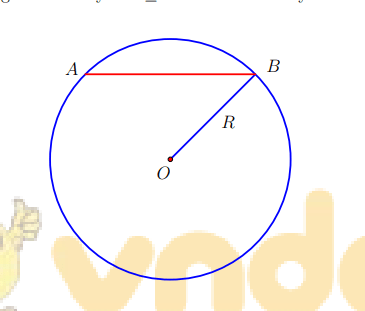
Vận dụng định lí đường kính và dây AB ≤ 2R.
Dấu ” = ” xảy ra khi A, O, B thẳng hàng.
• Vận dụng các bất đẳng thức đại số:
+) dấu ” = ” xảy ra khi a = b.
+) dấu ” = ” xảy ra khi a = b.
+) Bất đẳng thức tam giác (quy tắc ba điểm).
+) Quan hệ đường kính và dây cung.
+) Quan hệ đường vuông góc và đường xiên.
6. Tiếp tuyến của đường tròn.
a) Định nghĩa Tiếp tuyến của đường tròn là đường thẳng chỉ có một điểm chung với đường tròn đó.
b) Định lí 1 Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
c) Định lí 2 Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
d) Tính chất hai tiếp tuyến cắt nhau:
Định lí: Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
• Điểm đó cách đều hai tiếp điểm.
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tia tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm. 7. Các bước của phương pháp chứng minh đi qua một điểm cố định.
Bước 1: Xác định rõ các yếu tố cố định đã biết.
Bước 2: Xác định tứ giác nội tiếp liên quan đến điểm cố định.
Bước 3: Chứng minh đường thẳng hoặc đường tròn đi qua điểm cố định.
B. Nội dung kiến thức cần biết của học kì II.
1. Góc ở tâm
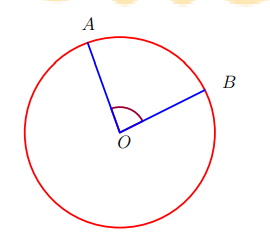
a. Định nghĩa
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.
b) Tính chất:
2. Liên hệ giữa cung và dây
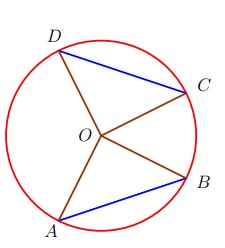
a) Hai cung bằng nhau căng hai dây bằng nhau.
b) Hai dây bằng nhau căng hai cung bằng nhau.
Định lí:
• Đường kính đi qua điểm chính giữa của một cung thì chia đôi dây căng cung. Đường kính đi qua trung điểm của một dây không đi qua tâ thi đi qua điểm chính giữa cung căng dây đó.
• Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
3. Góc nội tiếp
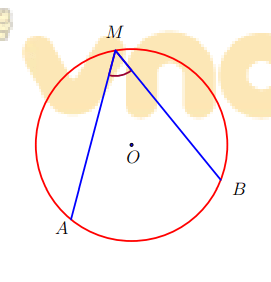
a) Định nghĩa Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
b) Tính chất .
4. Góc tạo bởi tia tiếp tuyến và dây cung
a) Định nghĩa
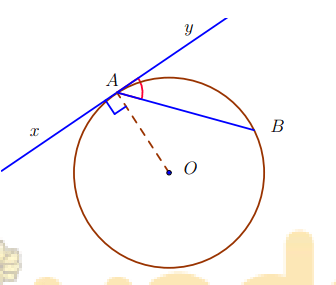
Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn và một cạnh là tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn đó.
Trong hình trên là hai góc tạo bởi tia tiếp tuyến và dây cung
cung lớn và
cung nhỏ.
b) Định lí
Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo góc của cung bị chắn.
c) Hệ quả
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
5. Góc có đỉnh ở bên trong đường tròn, góc có đỉnh ở bên ngoài đường tròn
a) Góc có đỉnh ở bên trong đường tròn
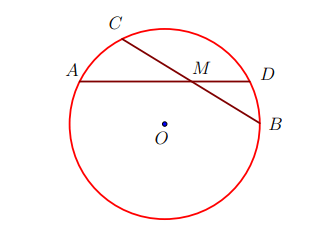
có đỉnh M nằm bên trong đường tròn
Định lí: Số đo góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
b) Góc có đỉnh nằm bên ngoài đường tròn
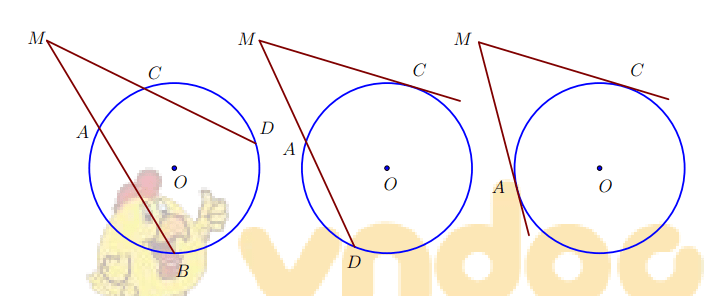
có đỉnh M nằm bên ngoài đường tròn
Định lí: Số đo góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
6. Cung chứa góc
a. Bài toán quỹ tích cung chứa góc
Với đoạn thẳng AB và góc α (00 < α < 1800) cho trước thì quỹ tích các điểm M thỏa mãn góc AMB = α là hai cung chứa góc α dựng trên đoạn AB.
Chú ý:
• Hai cung chứa góc α dựng trên đoạn AB là hai cùng tròn đối xứng nhau qua AB.
• Hai điểm A, B được coi là thuộc quỹ tích.
• Khi α = 900 thì quỹ tích các điểm nhìn đoạn AB cho trước dưới một góc vuông là đường tròn đường kính AB.
b) Cách giải bài toán quỹ tích
Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất (τ) là một hình H nào đó ta phải chứng minh hai phần:
Phần thuận: Mọi điểm có tính chất (τ) đều thuộc hình H.
Phần đảo: Mọi điểm thuộc hình H đều có tính chất (τ).
Kết luận: Quỹ tích (tập hợp) các điểm M có tính chất (τ) là hình H.
c) Dạng bài quỹ tích
Quỹ tích là cung chứa góc α
Phương pháp:
+) Tìm đoạn thẳng cố định trong hình vẽ.
+) Nối điểm phải tìm quỹ tích với hai đầu của đoạn thẳng cố định đó, xác định góc α tạo thành.
+) Khẳng định điểm phải tìm quỹ tích thuộc cung chứa góc α vẽ trên đoạn thẳng cố định.
7. Tứ giác nội tiếp
a) Định nghĩa
Tứ giác có 4 đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp.
b) Tính chất
Trong một tứ giác nội tiếp thì hai góc đối có tổng bằng 1800
Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1800 thì tứ giác đó nội tiếp đường tròn
c) Dấu hiệu nhau thì bốn đỉnh của tứ giác ấy cùng thuộc một đường tròn.
d. Vận dụng
Phương pháp:
Để chứng minh một tứ giác nội tiếp (hay 4 điểm cùng thuộc một đường tròn) ta cần:
(1) Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó.
(2) Chứng minh tứ giác có tổng 2 góc đối bằng 1800
(3) Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau.
(4) Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.
Cụ thể: Cho tam giác ABCD. Nếu các bạn chứng minh được thì tứ giác ABCD cũng nội tiếp trong một đường tròn.
Đây có thể nói là một trường hợp đặc biệt của trường hợp thứ 2.
• Trong một tứ giác nội tiếp thì hai góc đối có tổng bằng 1800.
• Nếu một tứ giác có tổng số đo hai góc đối diện bằng 1800 thì tứ giác đó nội tiếp đường tròn.
(5) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn.
(6) Chứng minh bằng phương pháp phản chứng.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu!
---------------------------------------------------------
Ngoài ra bạn đọc có thể tham khảo thêm các chuyên đề khác trong chương trình ôn thi vào lớp 10 được VnDoc sưu tầm và chọn lọc, bao gồm:
- Rút gọn biểu thức - Xem thêm Ôn thi vào lớp 10 chuyên đề: Rút gọn biểu thức và bài toán phụ
- Hàm số và đồ thị - Xem thêm Ôn thi vào lớp 10 chuyên đề: Hàm số và đồ thị
- Hệ phương trình - Xem thêm Ôn thi vào lớp 10 chuyên đề: Hệ phương trình bậc nhất hai ẩn
- Phương trình bậc hai một ẩn - Xem thêm Ôn thi vào lớp 10 chuyên đề: Phương trình bậc hai một ẩn
- Bất đẳng thức và tìm GTLN, GTNN - Xem thêm Ôn thi vào lớp 10 chuyên đề: Chứng minh bất đẳng thức và tìm GTLN, GTNN
Qua đó sẽ giúp các bạn học sinh kiểm tra kiến thức cũng như củng cố lại các kiến thức đã được học ở chương trình Toán học lớp 9. Đồng thời đây cũng là tài liệu để các bạn học sinh có thể tham khảo và ôn luyện chuẩn bị cho kì thi vào 10 sắp tới.
Ngoài Chuyên đề Hình học ôn thi vào lớp 10, mời các bạn học sinh tham khảo thêm các đề thi vào 10 các môn Toán, Văn, Anh,... mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề Toán lớp 9 ôn thi vào lớp 10 và làm bài tốt hơn. Chúc các bạn học tập tốt!
Xem thêm đề thi vào lớp 10 các môn Toán, Văn, Tiếng Anh:
| Môn Toán | Môn Văn | Môn Tiếng Anh |
| Tải đề thi vào lớp 10 môn Toán | Tải đề thi vào lớp 10 môn Văn | Tải đề thi vào lớp 10 môn Tiếng Anh |






