35 bài tập hệ thức lượng trong tam giác có hướng dẫn
35 bài tập hệ thức lượng trong tam giác
VnDoc xin giới thiệu tới bạn đọc bài viết 35 bài tập hệ thức lượng trong tam giác có hướng dẫn để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết.
Mời bạn đọc tham khảo tài liệu học tập Toán 10 theo bộ SGK chương trình mới của Bộ GD&ĐT:
Nhắc lại công thức hệ thức lượng trong tam giác
a. Định lí cosin
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai góc còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có hệ thức sau:
![]()
![]()
![]()
b. Tính độ dài đường trung tuyến của tam giác
Cho tam giác ABC có cạnh AB = c, AC = b, BC = a. Gọi độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác ABC là: ![]() ta có:
ta có:
![]()
![]()
![]()
c. Định lí sin
Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:
![]()
Với R là bán kính đường tròn ngoại tiếp tam giác
d. Công thức diện tích tam giác
Giả sử ![]() là các đường cao lần lượt kẻ từ đỉnh A, B, C của tam giác ABC.
là các đường cao lần lượt kẻ từ đỉnh A, B, C của tam giác ABC.
Diện tích tam giác ABC được tính theo một trong các công thức sau:

Với p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC
Bài tập hệ thức lượng trong tam giác
Bài 1. Cho ΔABC có AB = 12, BC = 15, AC = 13
a. Tính số đo các góc của ΔABC
b. Tính độ dài các đường trung tuyến của ΔABC
c. Tính diện tích tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC
d. Tính độ dài đường cao nối từ các đỉnh của tam giác ABC
Hướng dẫn giải
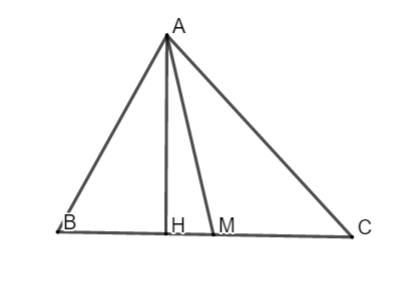
a. Áp dụng hệ thức lượng trong tam giác ta có:


Ta có tổng 3 góc của một tam giác là ![]()
![]()
b. Ta có: ![]()
![]()
Tương tự ta tính được:

c. Để tính được diện tích một cách chính xác nhất ta sẽ áp dụng công thức Hê – rông
- Nửa chu vi tam giác ABC: ![]()
- Diện tích tam giác ABC: ![]()
- Bán kính đường tròn ngoại tiếp R của tam giác ABC:

- Bán kính đường tròn nội tiếp r của tam giác ABC:

d. Ta có: ![]()

Bài 2. Cho ΔABC có AB = 6, AC = 8, góc A = 1200
a. Tính diện tích ΔABC
b. Tính cạnh BC và bán kính đường tròn ngoại tiếp của tam giác ABC
Hướng dẫn giải
a. Diện tích tam giác ABC: ![]()
b. Ta có:

- Bán kính đường tròn ngoại tiếp tam giác ABC:

Bài 3. Cho ΔABC có a = 8, b = 10, c = 13
a. ΔABC có góc tù hay không?
b. Tính bán kính đường tròn ngoại tiếp ΔABC
c. Tính diện tích ΔABC
HS: Tự giải
Bài 4. Cho ΔABC có góc A = 600, góc B = 450, b = 2. Tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp ΔABC và diện tích tam giác.
HS: Tự giải
Bài 5. Cho ΔABC: AC = 7, AB = 5. Tính BC, S, ha, R.
HS: Tự giải
Bài 6. Cho ΔABC có mb = 4, mc = 2 và a = 3, tính độ dài cạnh AB, AC.
HS: Tự giải
Bài 7. Cho ΔABC có AB = 3, AC = 4 và diện tích S = 3√3. Tính cạnh BC.
HS: Tự giải
Bài 8. Tính bán kính đường tròn nội tiếp ΔABC biết AB = 2, AC = 3, BC = 4
HS: Tự giải
Bài 9. Tính góc A của ΔABC có các cạnh a, b, c thỏa hệ thức b(b2 - a2) = c(a2 - c2)
HS: Tự giải
Bài 10. Cho ΔABC. Chứng minh rằng:
a. 
b. ![]()
c. ![]()
d. 
e. ![]()
f. ![]()
HS: tự giải
Bài 11. Gọi G là trọng tâm tam giác ABC và M là điểm tùy ý. Chứng minh rằng:
a. ![]()
b. ![]()
HS: tự giải
Bài 12. Cho tam giác ABC có b + c = 2a. Chứng minh rằng
a. ![]()
b. ![]()
HS: tự giải
Bài 13. Cho tam giác ABC biết ![]()
a. Tính các cạnh và các góc còn lại của tam giác ABC.
b. Tính chu vi và diện tích tam giác ABC.
HS: tự giải
Bài 14. Cho tam giác ABC biết ![]() . Tính
. Tính ![]() , cạnh b, c của tam giác đó.
, cạnh b, c của tam giác đó.
HS: tự giải
Bài 15. Cho tam giác ABC biết ![]() . Tính số đo các góc A, B và độ dài cạnh c.
. Tính số đo các góc A, B và độ dài cạnh c.
Bài 16. Để lấp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 10km, rồi nối từ vị trí C đến B dài 8km. Biết góc tạo bởi 2 đoạn dây AC và CB là ![]() . Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
HS: tự giải
Bài 17. 2 Vị trí A và B cách nhau 500m ở bên này bờ sông từ vị trí C ở bên kia bờ sông. Biết ![]() . Hãy tính khoảng cách AC và BC.
. Hãy tính khoảng cách AC và BC.
HS: tự giải
Bài 18. Cho tam giác ABC có BC = a, ![]() và hai đường trung tuyến BM và CN vuông góc với nhau. Tính diện tích tam giác ABC.
và hai đường trung tuyến BM và CN vuông góc với nhau. Tính diện tích tam giác ABC.
Hướng dẫn giải
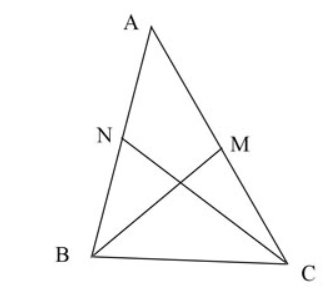
Hai đường trung tuyến BM và CN vuông góc với nhau thì 

Mặt khác ![]()

Bài 19: Cho tam giác ABC. Gọi ![]() lần lượt là độ dài các đường phân giác góc A, B, C. Chứng minh rằng:
lần lượt là độ dài các đường phân giác góc A, B, C. Chứng minh rằng:
a. ![]()
b. 
c. ![]()
Hướng dẫn giải

Trước hết chứng minh công thức ![]() bằng cách sử dụng tam giác cân tại đỉnh A có
bằng cách sử dụng tam giác cân tại đỉnh A có ![]() thông qua công thức diện tích để đi đến kết luận trên
thông qua công thức diện tích để đi đến kết luận trên
![]()
Mà ![]()
b. 







.........................................
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết 35 bài tập hệ thức lượng trong tam giác có hướng dẫn. VnDoc.com mời các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 10, đề thi học kì 2 lớp 10 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc.