Bài tập Toán có lời văn lớp 5
Bài tập Toán có lời văn lớp 5
Bài tập Toán có lời văn lớp 5 bao gồm các dạng Toán có lời văn từ cơ bản đến nâng cao được VnDoc sưu tầm, tổng hợp. Để học tốt môn Toán lớp 5 và để giúp các em học sinh ôn tập, củng cố kiến thức các dạng bài tập có lời văn, ôn luyện các dạng bài tập là nền tảng kiến thức quan trọng cho các lớp về sau. Sau đây mời các em cùng tham khảo và tải về bản chi tiết đầy đủ.
Lưu ý: Nếu không tìm thấy nút Tải về bài viết này, bạn vui lòng kéo xuống cuối bài viết để tải về.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 5, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 5 sau: Nhóm Tài liệu học tập lớp 5. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Bài Toán có lời văn lớp 5 giúp học sinh biết ứng dụng toán học vào cuộc sống. Các bài toán có lời văn là những miếng ghép quan trọng nối thế giới toán học với thế giới thực.
Các dạng Toán lớp 5 có lời văn lớp
+ Toán có lời văn về số phần trăm
+ Toán có lời văn về thể tích, diện tích
+ Quãng đường, vận tốc, thời gian
+ Chuyển động cùng chiều, ngược chiều
+ Các bài toán về chuyển động của tàu hỏa
+ Các bài toán chuyển động qui về bài toán tổng - tỉ, hiệu - tỉ
Dạng 1: Các bài Toán về trung bình cộng
Ví dụ: Trong 2 ngày Lan đọc xong một quyển truyện. Ngày thứ nhất Lan đọc được 20 trang, ngày thứ 2 đọc được 40 trang. Hỏi nếu mỗi ngày Lan đọc được số trang sách đều như nhau thì mỗi ngày Lan đọc được bao nhiêu trang sách?
Giáo viên cho học sinh đọc kĩ đầu bài. Tìm hiểu kĩ đề bài qua câu hỏi gợi ý:
Bài toán cho biết gì? (Lan đọc ngày 1 được 20 trang sách, ngày 2 được 40 trang sách)
Bài toán hỏi gì? (Tìm trung bình mỗi ngày lan đọc được bao nhiêu trang sách)
Ta có tóm tắt bài toán như thế nào là dễ hiểu và hợp lí, thuận tiện nhất? (vẽ sơ đồ)
Ta thấy bài toán ở dạng toán cơ bản nào ta đã được học? (Tìm số trung bình cộng)
Muốn giải và trình bày bài toán TBC ta làm như thế nào? (Tìm tổng các số hạng rồi chia cho số các số hạng)- ở bài này cụ thể ta cần tính 2 ngày Lan đọc được tất cả bao nhiêu trang sách lấy số nào để thực hiện (20 + 40), số các số hạng là mấy (2)
Lời giải
Ta có sơ đồ sau:
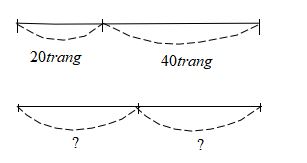
Số trang sách Lan đọc được trong hai ngày là:
20 + 40 = 60 (trang)
Số trang sách Lan đọc đều như nhau trong mỗi ngày là:
60 : 2 = 30 (trang)
Đáp số: 30 trang
Dạng 2: Ôn và giải toán tìm 2 số khi biết tổng và tỉ số của 2 số
Với dạng toán này học sinh thuộc các bước thực hiện giải toán, ở dạng toán này các em gặp khó khăn xác định đúng tỉ số và tổng để tìm lời giải ,đặc biệt với các bài có phép tính trung gian mới tìm được tỉ số hoặc tổng.
Những bài toán này học sinh lớp 5 thường có thể giải theo bài toán với phân số, nhưng bước quan trọng các em cần xác định được tỉ số để thiết lập được phân số để thực hiện được phép tính giải toán.
Bên cạnh đó các em còn sử dụng giải bằng phương pháp chia tỉ lệ.
Song dù giải bằng phương pháp nào các em cũng cần tìm ra tỉ số và xác định đúng tỉ số và tổng của hai số.
Ví dụ :
Một vườn hoa hình chữ nhật có chu vi là 120 m . Chiều rộng bằng 5/7 chiều dài.
a-Tính chiều dài, chiều rộng vườn hoa đó?
b- Người ta sử dụng 1/25 diện tích vườn hoa để làm lối đi. Hỏi diện tích lối đi là bao nhiêu mét vuông?
Với bài này các em cần cần tìm tổng chiều dài và chiều rộng (tức nửa chu vi) rồi sẽ tính được chiều dài, chiều rộng.
Tính được diện tích của vườn hoa, tính được diện tích lối đi có thể theo giải bài toán với phân số hay với toán tổng - tỉ đều được.
Nhưng với bài này học sinh thường nhầm lấy ngay chu vi để làm tính coi đó là tổng nên bài toán sai. Một số em khi đến bước tìm diện tích lối đi , các em không biết cần tìm diện tích của vườn hoa.
Khi hướng dẫn học sinh học sinh giải bài này yêu cầu học sinh cần đọc kĩ đề bài, xác định dữ kiện đã cho biết gì (chu vi 120 m, chiều rộng bằng 5/7 chiều dài, diện tích lối đi bằng diện tích thửa ruộng)? Hỏi gì (tính chiều dài chiều rộng và diện tích lối đi)? Ta có thể giải theo dạng toán cơ bản nào (tìm hai số biết tổng của hai số hay giải bài toán với phân số) ? có những cách giải nào? Chọn cách tóm tắt theo sơ đồ đoạn thẳng hay sơ đồ cây, nhìn vào sơ đồ các em nhận ra các bước giải, tìm và chọn cách giải phù hợp với mình và khoa học, nhanh nhất:
Giải
a-Nửa chu vi của thửa ruộng là:
120 : 2 = 60 (m)
Chiều rộng của thửa ruộng là:
60 : (5 + 7 ) x 5 = 25 (m)
Chiều dài của thửa ruộng là:
60 - 25 = 35 (m)
b- Diện tích của thửa ruộng là:
35 x 25 = 875 ( m2)
Diện tích lối đi là:
875 x ![]() \(\frac{1}{25}\) = 35 (m2 )
\(\frac{1}{25}\) = 35 (m2 )
Đáp số : a- Chiều rộng: 25 m
Chiều dài 35 m
b- 35 m2
Ngoài ra còn cho học sinh giải bài tập dưới dạng bài trắc nghiệm điền và chọn đúng sai, bài toán vui, toán cổ... .Với hình thức đa dạng hình thức bài tập gây hứng thú học tập cho học sinh, đồng thời rèn kĩ năng thực hiện và giải toán cho học sinh.
Chẳng hạn:
Chọn câu trả lời đúng :
Tổng của hai số là số nhỏ nhất có ba chữ số. Tỉ số của hai số là ![]() \(\frac{3}{7}\). Tìm hai số đó?
\(\frac{3}{7}\). Tìm hai số đó?
A 3 và 97
B 3 và 7
C 30 và 70
D 33 và 77 .
Hướng dẫn học sinh cách chọn nhanh :
Tổng của hai số là số có 3 chữ số nên hai số đó phải có ít nhất 1 số là số có hai chữ số nên chỉ có thể là 30 và 70 hay 33 và 77, 3 và 97. Dựa theo tỉ số thì 1 trong 2 số phải là số chia hết cho 10 và cho 3 nên chọn được ngay đáp số đúng là C.
b-Ôn tập giải bài toán tìm hai số biết hiệu và tỉ số của hai số:
Cách hướng dẫn và giải tương tự chỉ khác tìm hiệu số phần và cần xác định được hiệu của hai số.
Ở 2 dạng toán này, giáo viên cần cho học sinh phối hợp với phương pháp chia tỉ lệ, với phương pháp sơ đồ đoạn thẳng.
Kết luận:
Với dạng toán thứ hai này các em cần xác định đúng tổng(hiệu) của hai số phải tìm, tỉ số của hai số phải tìm.Phân tích lựa chọn nên giải theo phương pháp chia tỉ lệ hay phương pháp giải toán về phân số để nhanh, khoa học và phù hợp, trình bày ngắn gọn và dễ hiểu, phù hợp với lớp 5 nhất. Sau đó giải và trình bày bài .
Dạng 3 :Bài toán liên quan đến tỉ lệ
Dạng toán này học sinh có hai phương pháp giải:
+ Phương pháp rút về đơn vị
+ Phương pháp dùng tỉ số
Cần cho học sinh đây hiểu đây là hai phương pháp giải toán khác nhau nhưng đều dùng để giải một dạng toán về tương quan tỉ lệ ( thuận, nghịch). Dạng toán này thường có hai đại lượng biến thiên theo tương quan tỉ lệ (thuận hoặc nghịch), người ta thường cho biết hai giá trị của đại lượng này và một giá trị của đại lượng kia rồi bắt tìm giá trị thứ hai của đại lượng kia.Để tìm giá trị này thì dùng phương pháp rút về đơn vị hay tỉ số như sau:
a-Phương pháp rút về đơn vị :
Bước 1 : Rút về đơn vị : trong bước này ta tính một đơn vị của đại lượng thứ nhất ứng với bao nhiêu đơn vị của đại lượng thứ hai hoặc ngược lại .
Bước 2 : Tìm giá trị chưa biết của đại lượng thứ hai.Trong bước này lấy giá trị của đại lượng thứ hai tương ứng với một đơn vị của đại thứ nhất (vừa tìm được ở bước 1)nhân với (hoặc chia cho) giá trị còn lại của đại lượng thứ nhất.
b-Phương pháp tỉ số:
Khi giải bài toán này ta tiến hành :
Bước 1 : Tìm tỉ số: Ta xác định trong hai giá trị đã cho của đại lượng thứ nhất thì giá trị này gấp hoặc kém giá trị kia mấy lần .
Bước 2; Tìm giá trị chưa biết của đại lượng thứ hai.
Ví dụ :
Bài 1:
Để hút hết nước ở một cái hồ, phải dùng 3 máy bơm làm việc liên tục trong 4 giờ. Vì muốn công việc hoàn thành sớm hơn người ta dùng 6 máy bơm nước như thế. Hỏi sau mấy giờ sẽ hút hết nước ở hồ?
Phân tích :
Trong bài này ta thấy có 3 đại lượng: Nước ở hồ là đại lượng không đổi.
Số máy bơm và thời gian là hai đại lượng biến thiên theo tỉ lệ nghịch ?
Ta thấy :
3 máy bơm hút hết 4 giờ.
1 máy bơm hút hết ? giờ.
6 máy bơm hút hết ? giờ.
Bài này ta có thể giải được bằng cả hai phương pháp. Chẳng hạn:
Phương pháp dùng rút về đơn vị:
Học sinh đọc đề và phân tích như trên để tìm hiểu đề và tóm tắt sau đó giải như sau:
1 máy bơm hút cạn nước hồ cần thời gian là :
4 x 3 = 12( giờ )
6 máy bơn hút cạn hồ nước hết thời gian là:
12 : 6 = 2 (giờ)
Đáp số : 2 giờ
Phương pháp dùng tỉ số:
Học sinh tìm xem số máy bơm tăng lên so với lúc đầu mấy lần , thì thời gian bơm sẽ giảm đi bấy nhiêu lần và giải như sau :(Vì hai đại lượng số máy bơm và thời gian là hai đại lượng biến thiên theo tỉ lệ nghịch)
6 máy bơm so với 3 máy bơm lớn gấp:
6 : 3 = 2 (lần)
Thời gian để 6 máy bơm hút cạn nước hồ là :
4 : 2 = 2 (giờ).
Đáp số : 2 giờ
Dạng 4: Toán về tỉ số phần trăm
Với dạng toán này học sinh vận dụng tính tỉ số phần trăm của 2 số, tìm một số khi biết giá trị phần trăm của số đó.
Giáo viên cần cho học sinh hiểu thế nào là tỉ số phần trăm , giá trị của đại lượng đó là 100%. Từ đó có cách làm tương ứng cho mỗi bài tập.
Ví dụ:
Một người bỏ ra 42 000 đồng tiền vốn mua rau. Sau khi bán rau người đó thu được
52 500 đồng.Hỏi:
a- Tiền bán rau bằng bao nhiêu phần trăm tiền vốn?
b- Người đó đã lãi bao nhiêu phần trăm?
Phân tích:
a-Để tìm được số tiền bán rau bằng bao nhiêu phần trăm tiền vốn chính là đi tìm tỉ số phần trăm của tiền vốn và tiền sau khi bán thu được.
b- Chính là tìm tỉ số của số tiền lãi với tiền vốn.
Qua đó ta thấy cần biết giá trị nào là tiền vốn(42 000 đồng), giá trị nào là tiền sau khi bán (52 500 đồng).
Giải :
a-Số phần trăm của tiền bán rau và tiền vốn là:
52 500: 42 000 = 1,25
1,25 = 125 %
b- Tỉ số tiền vốn là 100% thì số tiền bán rau là 125%. Do đó số lãi là:
125% - 100% = 25%
Đáp số a- 125%, b- 25%
Ví dụ 2 :
Cuối năm 2000 số dân của một phường là 15 625 người.Cuối năm 2001 số dân của phường đó là 15 875 người.
Hỏi :
a-Từ cuối năm 2000 đến cuối năm 2001 số dân của phường đó tăng thêm bao nhiêu phần trăm?
b-Nếu từ cuối năm 2001 đến cuối năm 2002 số dân của phường đó cũng tăng bấy nhiêu phần trăm thì cuối năm 2002 số dân của phường đó là bao nhiêu người?
Phân tích:
Để tìm được số dân tăng thêm năm 2001 là bao nhiêu % ta cần tìm được số dân tăng là bao nhiêu người?
Tìm số người tăng thêm của năm 2002, mới tìm được số người dân cuối năm 2002 của phường đó.
Từ đó học sinh tìm ra các phép tính tương ứng và giải:
a-Từ cuối năm 2000 đến cuối năm 2001 số người tăng thêm là:
15875 - 15 625 - 250 (người)
Tỉ số phần trăm số dân tăng thêm là:
250 : 15 635 = 0,016
0,016 = 1,6%
b- Từ cuối năm 2001 đến cuối năm 2002 số người tăng thêm là:
15875 x 1,6 : 100 = 254 (người)
Cuối năm 2002 số dân của phường đó là:
15875 + 254 = 16 129 (người).
Đáp số : a- 1,6%.
b- 16 129 người.


