Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 - Cánh diều
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Tìm m để hàm số có hai cực trị

    Cho hàm số y = f(x) = x^{3} - 3mx^{2} + 4m^{2} - 2(*). Tìm tất cả các giá trị của m để hàm số (*) có hai điểm cực trị?

    Hướng dẫn:

    Ta có: y' = 3x^{2} - 6mx

    y' = 0 \Leftrightarrow 3x^{2} - 6mx = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2m \\ \end{matrix} ight.

    Để hàm số có hai cực trị thì phương trình y' = 0 có hai nghiệm phân biệt \Leftrightarrow 2m eq 0 \Leftrightarrow m eq 0.

    Vậy đáp án cần tìm là m eq 0.

  • Câu 2: Nhận biết
    Xác định các đường tiệm cận của đồ thị hàm số

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash\left\{ - 1 ight\} liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

    Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

    Hướng dẫn:

    Từ bảng biến thiên ta thấy:

    \lim_{x ightarrow - 1^{+}}y = - \infty suy ra x = - 1 là tiệm cận đứng.

    \lim_{x ightarrow - \infty}y = 2 suy ra y = 2 là tiệm cận ngang

    \lim_{x ightarrow - \infty}y = - 1 suy ra y = - 1 là tiệm cận ngang

    Vậy đồ thị hàm số đã cho có tất cả ba đường tiệm cận.

  • Câu 3: Thông hiểu
    Chọn đáp án đúng

    Cho hàm số y = f(x) = x^{3} - 3mx^{2} + 3\left( m^{2} - 1 ight)x với m là tham số. Tìm tất cả các giá trị của m để hàm số f(x) đạt cực đại tại x_{0} = 1?

    Hướng dẫn:

    Hàm số đạt cực đại tại x_{0} = 1

    \Leftrightarrow \left\{ \begin{matrix} f'(1) = 0 \\ f''(1) < 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 3 - 6m + 3m^{2} - 3 = 0 \\ 6 - 6m < 0 \\ \end{matrix} ight. \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} m = 0 \\ m = 2 \\ \end{matrix} ight.\ \\ m > 1 \\ \end{matrix} ight.\ \Leftrightarrow m = 2

    Vậy đáp án cần tìm là m = 2.

  • Câu 4: Thông hiểu
    Tìm giá trị lớn nhất nhỏ nhất của hàm số

    Cho hàm số f(x) = \frac{2x^{2} + x + 1}{x + 1}. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn \lbrack 0;1brack.

    Hướng dẫn:

    Đạo hàm f'(x) = \frac{2x^{2} + 4x}{(x+ 1)^2}.

    Ta có \left\{ \begin{matrix} f'(x) \geq 0,\ \forall x \in \lbrack 0;1brack \\ f'(x) = 0 \Leftrightarrow x = 0 \\ \end{matrix} ight..

    Suy ra hàm số f(x) đồng biến trên đoạn \lbrack 0;1brack.

    Vậy \left\{ \begin{matrix} M = \max_{\lbrack 0;1brack}f(x) = f(1) = 2 \\ m = \min_{\lbrack 0;1brack}f(x) = f(0) = 1 \\ \end{matrix} ight.

  • Câu 5: Vận dụng
    Xét tính đúng sai của các khẳng định

    Cho hàm số f(x) có đạo hàm f'(x) = (x - 1)^{2}\left( x^{2} - 3x + 2 ight) với mọi x\mathbb{\in R}.

    a) Phương trình f'(x) = 0 có duy nhất một nghiệm x = 2. Sai||Đúng

    b) Hàm số f(x) đồng biến trên khoảng ( - 3;0). Đúng||Sai

    c) Hàm số f(x) có hai điểm cực trị. Đúng||Sai

    d) Hàm số y = f\left( x^{2} - 6x + 1 ight) có ba điểm cực đại. Sai||Đúng

    Đáp án là:

    Cho hàm số f(x) có đạo hàm f'(x) = (x - 1)^{2}\left( x^{2} - 3x + 2 ight) với mọi x\mathbb{\in R}.

    a) Phương trình f'(x) = 0 có duy nhất một nghiệm x = 2. Sai||Đúng

    b) Hàm số f(x) đồng biến trên khoảng ( - 3;0). Đúng||Sai

    c) Hàm số f(x) có hai điểm cực trị. Đúng||Sai

    d) Hàm số y = f\left( x^{2} - 6x + 1 ight) có ba điểm cực đại. Sai||Đúng

    a) Sai

    Ta có f'(x) = (x - 1)^{2}\left( x^{2} - 3x + 2 ight) = (x - 1)^{3}(x - 2).

    f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 2 \\ \end{matrix} ight..

    Vậy phương trình f'(x) = 0 có hai nghiệm.

    b) Đúng

    Bảng biến thiên y = f(x)

    Dựa vào bảng biến thiên của hàm số y = f(x) ta thấy hàm số đồng biến trên các khoảng ( - \infty;1),(2; + \infty).

    Ta có ( - 3;0) \subset ( - \infty;1) nên hàm số f(x) đồng biến trên khoảng ( - 3;0).

    c) Đúng

    Dựa vào bảng biến thiên của hàm số y = f(x) ta thấy hàm số có hai điểm cực trị.

    d) Sai

    Ta có:

    y = f\left( x^{2} - 6x + 1 ight)

    \Rightarrow y^{'} = \left( x^{2} - 6x + 1 ight)^{'}f^{'\left( x^{2} - 6x + 1 ight)} = (2x - 6)f'\left( x^{2} - 6x + 1 ight).

    y' = 0 \Leftrightarrow (2x - 6)f'\left( x^{2} - 6x + 1 ight) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} 2x - 6 = 0 \\ x^{2} - 6x + 1 = 1 \\ x^{2} - 6x + 1 = 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 3 \\ x = 0 \\ x = 6 \\ x = - 3 + \sqrt{10} \\ x = - 3 - \sqrt{10} \\ \end{matrix} ight..

    Bảng biến thiên y = f\left( x^{2} - 6x + 1 ight)

    Dựa vào bảng biến thiên của hàm số y = f\left( x^{2} - 6x + 1 ight) ta thấy hàm số có hai điểm cực đại.

  • Câu 6: Thông hiểu
    Chọn đáp án đúng

    Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số y = \frac{x - 1}{x^{2} - 8x + m} có ba đường tiệm cận?

    Hướng dẫn:

    Ta có: \lim_{x ightarrow \pm \infty}\frac{x - 1}{x^{2} - 8x + m} = 0 nên suy ra hàm số có 1 đường tiệm cận ngang là y = 0

    Để đồ thị hàm số có 3 đường tiệm cận thì phải có 2 tiệm cận đứng hay phương trình x^{2} - 8x + m = 0 có hai nghiệm phân biệt khác 1

    \left\{ \begin{matrix} 16 - m > 0 \\ 1^{2} - 8.1 + m eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m < 16 \\ m eq 7 \\ \end{matrix} ight.

    Do m nguyên dương nên có 14 giá trị m thỏa mãn.

  • Câu 7: Nhận biết
    Xác định tính đúng sai của từng phương án

    Cho hàm số y = f(x) xác định trên tập D và một số thực M. Xét tính đúng sai của các khẳng định sau:

    a) Nếu f(x) \leq M,\forall x \in D thì \underset{D}{\max f(x)} = M. Sai|| Đúng

    b) Nếu f(x) \geq M,\forall x \in D thì \underset{D}{\min f(x)} = M. Sai|| Đúng

    c) Nếu f(x) = M,\forall x \in D thì \underset{D}{\max f(x)} = M. Đúng||Sai

    d) Nếu f(x) = M,\forall x \in D thì \underset{D}{\min f(x)} = M. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) xác định trên tập D và một số thực M. Xét tính đúng sai của các khẳng định sau:

    a) Nếu f(x) \leq M,\forall x \in D thì \underset{D}{\max f(x)} = M. Sai|| Đúng

    b) Nếu f(x) \geq M,\forall x \in D thì \underset{D}{\min f(x)} = M. Sai|| Đúng

    c) Nếu f(x) = M,\forall x \in D thì \underset{D}{\max f(x)} = M. Đúng||Sai

    d) Nếu f(x) = M,\forall x \in D thì \underset{D}{\min f(x)} = M. Đúng||Sai

    a) Khẳng định này sai, cần bổ sung thêm điều kiện \exists x_{0} \in D để f\left( x_{0} ight) = M.

    b) Khẳng định này sai, cần bổ sung thêm điều kiện \exists x_{0} \in D để f\left( x_{0} ight) = M.

    c) Nếu f(x) = M,\forall x \in D thì f(x) là hàm hằng trên D (đồ thị là đường thẳng nằm ngang).

    Suy ra \underset{D}{\max f(x)} = M.

    d) Nếu f(x) = M,\forall x \in D thì f(x) là hàm hằng trên D (đồ thị là đường thẳng nằm ngang).

    Suy ra\underset{D}{\min f(x)} = M.

  • Câu 8: Nhận biết
    Tìm vận tốc tức thời của chuyển động

    Một vật chuyển động có quãng đường được xác định bởi phương trình s(t) = 2t^{2} + 5t + 2, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời tại thời điểm t = 4.

    Hướng dẫn:

    Ta có s'(t) = 4t + 5,s'(4) = 21m/s

  • Câu 9: Nhận biết
    Tìm khoảng đồng biến của hàm số

    Cho hàm số y = f(x) xác định trên \mathbb{R} và có bảng biến thiên như hình bên dưới

    Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

    Hướng dẫn:

    Dựa vào bảng biến thiên, ta thấy hàm số đồng biến trên (3; + \infty).

  • Câu 10: Vận dụng
    Tìm m để đồ thị có 1 tiệm cận ngang

    Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = \frac{x - 3}{x + \sqrt{mx^{2} + 4}} có đúng một tiệm cận ngang.

    Hướng dẫn:

    Ta có:

    \lim_{x ightarrow + \infty}y = \lim_{x ightarrow + \infty}\frac{x - 3}{x + \sqrt{mx^{2} + 4}} = \frac{1}{1 + \sqrt{m}} với m \geq 0;

    \lim_{x ightarrow - \infty}y = \lim_{x ightarrow - \infty}\frac{x - 3}{x + \sqrt{mx^{2} + 4}} = \frac{1}{1 - \sqrt{m}} với m \geq 0,m eq 1.

    Nếu m = 1 thì \lim_{x ightarrow - \infty}y = \lim_{x ightarrow - \infty}\frac{(x - 3)\left( \sqrt{x^{2} + 4} - x ight)}{4}= \lim_{x ightarrow - \infty}x^{2}.\frac{\left( 1 - \frac{3}{x} ight)\left( - \sqrt{1 + \frac{4}{x^{2}}} - 1 ight)}{4} = - \infty suy ra hàm số chỉ có đúng một TCN là y = \frac{1}{2} (Do\lim_{x ightarrow + \infty}y = \frac{1}{2} khi m = 1)

    Do đó giá trị m = 1 thỏa yêu cầu bài toán.

    Nếu \left\{ \begin{matrix} m \geq 0 \\ m eq 1 \\ \end{matrix} ight., để đồ thị hàm số có một tiệm cận ngang \Leftrightarrow \frac{1}{1 + \sqrt{m}} = \frac{1}{1 - \sqrt{m}} \Leftrightarrow m = 0.

    Vậy m = 0,m = 1 thỏa mãn yêu cầu bài toán.

  • Câu 11: Nhận biết
    Tìm số cực trị của hàm số

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = {x^2}\left( {x - 1} ight)\left( {x - 2} ight)\left( {{3^x} - 1} ight),\forall x \in \mathbb{R}. Số điểm cực trị của hàm số đã cho bằng

    Hướng dẫn:

     Ta có:

    f'\left( x ight) = 0 \Leftrightarrow {x^2}\left( {x - 1} ight)\left( {x - 2} ight)\left( {{3^x} - 1} ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1} \\ {x = 0} \\ {x = 2} \end{array}} ight.

    => Hàm số có 3 điểm cực trị

  • Câu 12: Thông hiểu
    Chọn phương án thích hợp

    Một cửa hàng trà sữa có đồ thị biểu diễn số ly trà sữa bán được trong một tuần như sau. Số ly trà sữa cửa hàng đó bán được nhiều nhất trong một ngày là bao nhiêu

    Hướng dẫn:

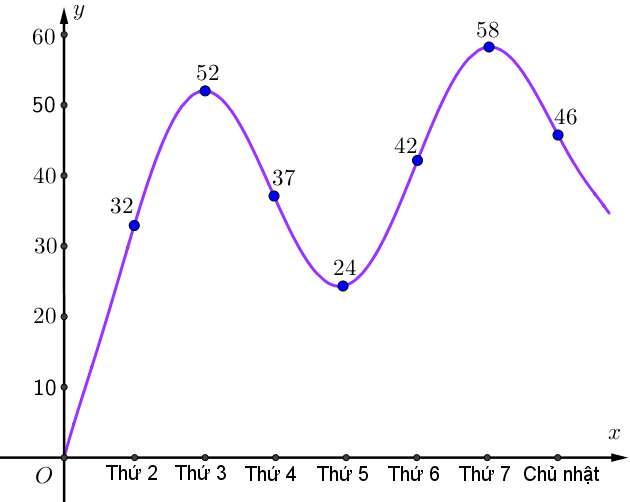
    Từ đồ thị ta thấy vào thứ 7 cửa hàng bán được nhiều nhất là 58 ly trà sữa.

  • Câu 13: Nhận biết
    Chọn khẳng định đúng

    Cho hàm số y = f(x) có \lim_{x ightarrow + \infty}f(x) = 0 và \lim_{x ightarrow - \infty}f(x) = + \infty. Khẳng định nào sau đây là khẳng định đúng?

    Hướng dẫn:

    Ta có \lim_{x ightarrow + \infty}f(x) = 0\overset{}{ightarrow}y = 0 là tiệm cận ngang.

    Đáp án “Đồ thị hàm số nằm phía trên trục hoành.“ sai vì chọn hàm y = \left\{ \begin{matrix} \left( \dfrac{1}{2} ight)^{x} & ;x \leq - 1 \\ - \left( \dfrac{1}{2} ight)^{x} & ;x \geq 1 \\ \end{matrix} ight..

    Vậy ta chỉ có đáp án “Đồ thị hàm số có một tiệm cận ngang là trục hoành” đúng.

  • Câu 14: Nhận biết
    Tìm hàm số đồng biến trên R

    Trong các hàm số dưới đây, hàm số nào đồng biến trên \mathbb{R}?

    Hướng dẫn:

     Hàm số y = x – sinx có tập các định D = \mathbb{R} và y' = 1 - \cos x \geqslant 0, \vee x \in \mathbb{R}

    Nên hàm số luôn đồng biến trên \mathbb{R}

  • Câu 15: Thông hiểu
    Viết biểu thức tính L(x) theo x

    Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được xmét vải lụa 1 \leq x \leq 18.Tổng chi phí sản xuất xmét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:

    C(x) = x^{3} - 6x^{2} + 20x + 500

    Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 320 nghìn đồng/mét. Gọi L(x)là lợi nhuận thu được khi bán xmét vải lụa. Hãy viết biểu thức tính L(x)theo\ x?

    Hướng dẫn:

    Khi bán x mét vải lụa

    Số tiền thu được là: B(x) = 320x .

    Lợi nhuận thu được là: L(x) = B(x) - C(x) = - x^{3} + 6x^{2} + 300x - 500.

  • Câu 16: Thông hiểu
    Định m để hàm số nghịch biến trên R

    Cho hàm số y = - x^{3} - 3(m + 1)x^{2} + 3(2m - 1)x + 2020. Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên ( - \infty; + \infty)?

    Hướng dẫn:

    Ta có: y' = - 3x^{2} - 6(m + 1)x + 3(2m - 1)

    Để hàm số đã cho nghịch biến trên ( - \infty; + \infty)

    \Leftrightarrow y' \leq 0 \Leftrightarrow \Delta' \leq 0

    \Leftrightarrow 9\left( m^{2} + 2m + 1 ight) + 18m - 9 \leq 0

    \Leftrightarrow 9m^{2} + 36m \leq 0 \Leftrightarrow - 4 \leq m \leq 0

    Do m\mathbb{\in Z} nên có tất cả 5 giá trị của m thỏa mãn điều kiện.

  • Câu 17: Vận dụng cao
    Tính GTNN của biểu thức

    Cho x, y là các số thực thỏa mãn {\left( {x - 3} ight)^2} + {\left( {y - 1} ight)^2} = 5. Giá trị nhỏ nhất của biểu thức P = \frac{{3{y^2} + 4xy + 7x + 4y - 1}}{{x + 2y + 1}} bằng:

    Hướng dẫn:

    \begin{matrix} {\left( {x - 3} ight)^2} + {\left( {y - 1} ight)^2} = 5 \hfill \\ \Rightarrow {x^2} + {y^2} - 6x - 2y + 5 = 0 \hfill \\ P = \dfrac{{\left( {3{y^2} + 4xy + 7x - 4y - 1} ight) + \left( {{x^2} + {y^2} - 6x - 2y + 5} ight)}}{{x + 2y + 1}} \hfill \\ P = \dfrac{{4{y^2} + 4xy + {x^2} + x + 2y + 4}}{{x + 2y + 1}} \hfill \\ P = \dfrac{{{{\left( {2y + x} ight)}^2} + \left( {x + 2y} ight) + 4}}{{x + 2y + 1}} \hfill \\ \end{matrix}

    Đặt t = x + 2y

    \begin{matrix} \left( {{1^2} + {2^2}} ight)\left[ {{{\left( {x - 3} ight)}^2} + {{\left( {y - 1} ight)}^2}} ight] \geqslant {\left[ {\left( {x - 3} ight) + \left( {2y - 2} ight)} ight]^2} \hfill \\ \Rightarrow {\left( {x + 2y - 5} ight)^2} \leqslant 25 \hfill \\ \Leftrightarrow 0 \leqslant x + 2y \leqslant 10 \hfill \\ \end{matrix}

    Ta được P = f\left( t ight) = \frac{{{t^2} + t + 4}}{{1 + 4}} = t + \frac{4}{{t + 1}};0 \leqslant t \leqslant 10

    Xét f'\left( t ight) = 1 - \frac{4}{{{{\left( {t + 1} ight)}^2}}} = 0 \Rightarrow {\left( {t + 1} ight)^2} = 4 \Rightarrow \left[ {\begin{array}{*{20}{c}} {t = 1\left( {tm} ight)} \\ {t = - 3\left( L ight)} \end{array}} ight.

    Vì f\left( 0 ight) = 4;f\left( {10} ight) = \frac{{114}}{{11}};f\left( 1 ight) = 3 \Rightarrow \min P = 3{\text{ khi t = 1}}

  • Câu 18: Nhận biết
    Tìm giá trị cực tiểu của hàm số

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Xác định giá trị cực tiểu của hàm số đã cho.

    Hướng dẫn:

    Dựa vào bảng biến thiên ta thấy:

    Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu là y = 1.

  • Câu 19: Vận dụng
    Định số lượng sản phẩm theo yêu cầu

    Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x^{2} + 10x + 5(triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là f(x) = \frac{C(x)}{x}. Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?

    Hướng dẫn:

    Khảo sát sự biến thiên của hàm số y = f(x) = \frac{C(x)}{x} = \frac{0,2x^{2} + 10x + 5}{x}.

    Tập xác định: \lbrack 1; + \infty).

    Sự biến thiên: Ta có f(x) = 0,2x + 10 + \frac{5}{x}.

    - f'(x) = \frac{0,2x^{2} - 5}{x^{2}},f^{'}(x) = 0 \Leftrightarrow x = 5 (do x \geq 1 ).

    - Hàm số f(x) đồng biến trên khoảng (5; + \infty), nghịch biến trên khoàng (1;5).

    - Hàm số f(x) đạt cực tiều tại x = 5 với f_{CT} = 12.

    - Giới hạn tại vô cực: \lim_{x \rightarrow + \infty}f(x) = + \infty.

    Bảng biến thiên:

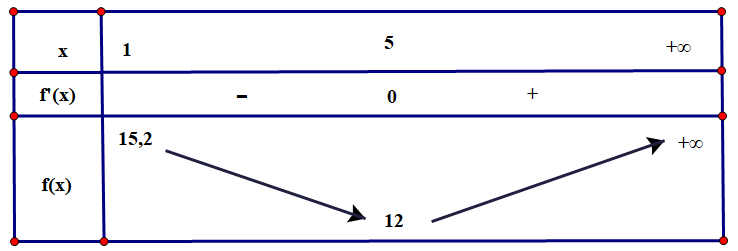
    Số lượng sản phẩm cần sản xuất là x = 5 để chi phí trung bình là thấp nhất

  • Câu 20: Nhận biết
    Tìm vận tốc tức thời của vật

    Một vật rơi tự do có phương trình chuyển động là s(t) = \frac{1}{2}gt^{2}, trong đó g = 9,8m/s^{2}. Tìm thời điểm mà vận tốc tức thời của vật tại thời điểm đó bằng 39,2(m/s).

    Hướng dẫn:

    Thật vậy: v(t) = s'(t) = 9,8t.

    Ta có: v(t) = 9,8t = 39,2 \Leftrightarrow t = 4.

    Vậy vận tốc tức thời của vật đạt 39,2(m/s) tại thời điểm t = 4(s).

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (45%):
    2/3
  • Thông hiểu (35%):
    2/3
  • Vận dụng (15%):
    2/3
  • Vận dụng cao (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
30 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Toán 12 - Cánh diều
Xem thêm