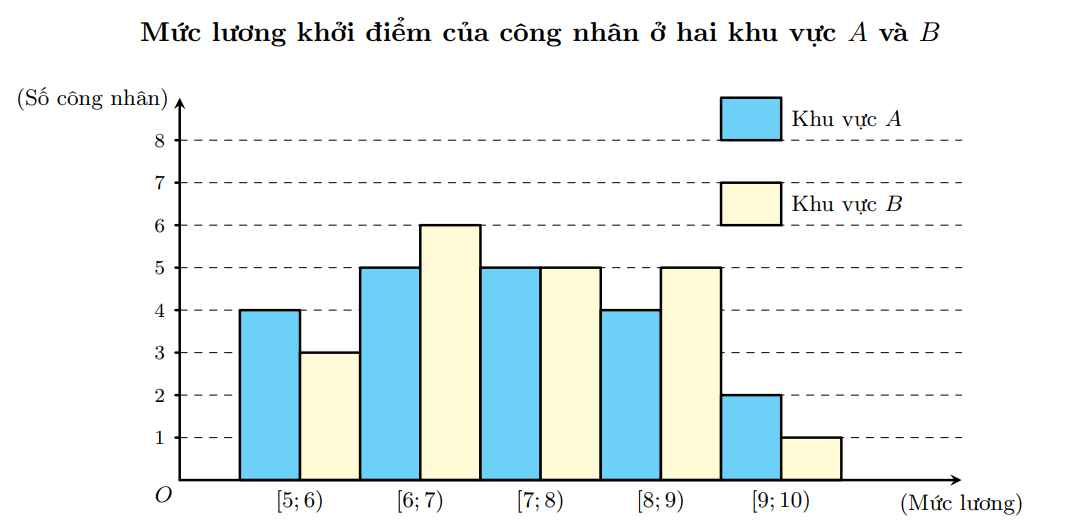
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm
Thống kê tổng số giờ nắng trong tháng ![]() tại một trạm quan trắc đặt ở Cà Mau trong các năm từ
tại một trạm quan trắc đặt ở Cà Mau trong các năm từ ![]() đến
đến ![]() được thống kê như sau:
được thống kê như sau:
|
Số giờ nắng |
|||||
|
Số năm |
3 |
6 |
3 |
5 |
3 |
Độ lệch chuẩn của mẫu số liệu là (kết quả làm tròn đến hàng phần nghìn)
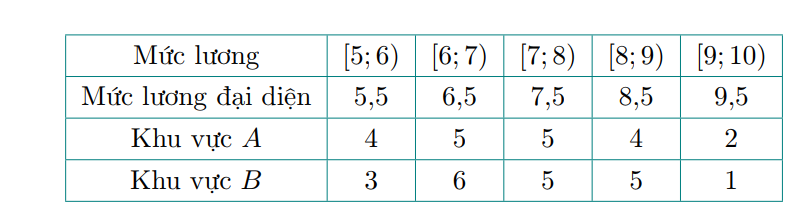
Ta có bảng sau:
|
Số giờ nắng |
|||||
|
Giá trị đại diện |
89 | 107 | 125 | 143 | 161 |
|
Số năm |
3 |
6 |
3 |
5 |
3 |
Số trung bình của mẫu số liệu là
Phương sai của mẫu số liệu ghép nhóm là
Độ lệch chuẩn của mẫu số liệu ghép nhóm là