Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 - Cánh diều
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân Cánh Diều

Mô tả thêm:

Trong chương trình Toán 12 Cánh Diều, Chương 4 về Nguyên hàm – Tích phân là phần kiến thức quan trọng, gắn liền với nhiều ứng dụng trong giải tích và bài toán thực tế. Đây cũng là nội dung thường xuyên xuất hiện trong các bài kiểm tra và đề thi. Việc luyện tập với đề kiểm tra 15 phút Chương 4 Nguyên hàm – Tích phân sẽ giúp học sinh hệ thống hóa công thức, rèn luyện kỹ năng tính toán và làm quen với các dạng bài tiêu biểu. Bài viết này giới thiệu đến bạn đề kiểm tra 15 phút Toán 12 Cánh Diều kèm lời giải chi tiế
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Nhận biết

    Tính giá trị biểu thức

    Cho hàm số F(x) là một nguyên hàm của f(x) = \frac{1}{2x - 1} , biết rằng F(1) = 2. Khi đó giá trị F(2) là:

    Ta có: F(x) = \int_{}^{}\frac{dx}{2x - 1} = \frac{1}{2}\ln|2x - 1| + C;\left( C\mathbb{\in R} ight)

    Mà F(1) = 2 \Rightarrow C = 2. Vậy với x > \frac{1}{2} thì F(x) = \frac{1}{2}\ln(2x - 1) + 2

    Vậy F(2) = \frac{1}{2}\ln3 +2.

  • Câu 2: Nhận biết

    Chọn đáp án đúng

    Nguyên hàm \int_{}^{}{\left( sin2x + \cos x \right)dx} là:

    Ta có:

    \int_{}^{}{\left( sin2x + \cos x \right)dx} = - \frac{1}{2}cos2x + \sin x + C.

  • Câu 3: Thông hiểu

    Tính giá trị biểu thức

    Thể tích khối tròn xoay khi quay hình phẳng (S) giới hạn bởi các đường y = 4 - x^{2};y = 0 quanh trục Ox có kết quả có dạng \frac{\pi a}{b} với a;b là các số nguyên dương và \frac{a}{b} là phân số tối giản. Khi đó giá trị của a - 30b bằng:

    Phương trình hoành độ giao 4 - x^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 \\ x = 2 \\ \end{matrix} ight.

    Thể tích cần tính V = \pi\int_{- 2}^{2}{\left( 4 - x^{2} ight)^{2}dx} = \left. \ \left( \frac{x^{5}}{5} - \frac{8x^{3}}{3} - 16x ight) ight|_{- 2}^{2} = \frac{512\pi}{15}

    Suy ra a = 512;b = 15 \Rightarrow a - 30b = 62.

  • Câu 4: Vận dụng

    Tính thể tích của vật thể

    Cho một mô hình 3 - D mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài 5\ (cm); khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thứcy = 3 - \frac{2}{5}x (cm), với x(cm) là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị cm^{3}) không gian bên trong đường hầm mô hình (làm tròn kết quả đến hàng đơn vị )

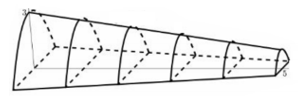
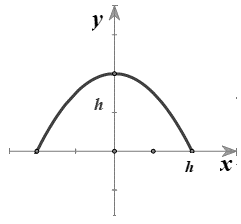
    Xét một thiết diện parabol có chiều cao là h và độ dài đáy 2h và chọn hệ trục Oxy như hình vẽ trên.

    Parabol (P) có phương trình (P):y = ax^{2} + h,(a < 0)

    Có B(h;0) \in (P) \Leftrightarrow 0 = ah^{2} + h \Leftrightarrow a = - \frac{1}{h}(do\ h > 0)

    Diện tích S của thiết diện: S = \int_{- h}^{h}{\left( - \frac{1}{h}x^{2} + h \right)dx} = \frac{4h^{2}}{3}, h = 3 - \frac{2}{5}x

    \Rightarrow S(x) = \frac{4}{3}\left( 3 - \frac{2}{5}x \right)^{2}

    Suy ra thể tích không gian bên trong của đường hầm mô hình: V = \int_{0}^{5}{S(x)dx} = \int_{0}^{5}{\frac{4}{3}\left( 3 - \frac{2}{5}x \right)^{2}dx} \approx 28,888

    \Rightarrow V \approx 29\ \ \left( cm^{3} \right)

  • Câu 5: Thông hiểu

    Xét tính đúng sai của các khẳng định

    Một ô tô đang chạy đều với vận tốc x m/s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = - 5t + 20 m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.

    a) Khi xe dừng hẳn thì vận tốc bằng 0 m/s. Đúng||Sai

    b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5s. Sai||Đúng

    c) \int_{}^{}{( - 5t + 20)dt} = \frac{- 5t^{2}}{2} + 20t + C. Đúng||Sai

    d) Quãng đường từ lúc đạp phanh cho đến khi xe đừng hẳn là 400m. Sai||Đúng

    Đáp án là:

    Một ô tô đang chạy đều với vận tốc x m/s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v(t) = - 5t + 20 m/s, trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh.

    a) Khi xe dừng hẳn thì vận tốc bằng 0 m/s. Đúng||Sai

    b) Thời gian từ lúc người lái xe đạp phanh cho đến khi xe dừng hẳn là 5s. Sai||Đúng

    c) \int_{}^{}{( - 5t + 20)dt} = \frac{- 5t^{2}}{2} + 20t + C. Đúng||Sai

    d) Quãng đường từ lúc đạp phanh cho đến khi xe đừng hẳn là 400m. Sai||Đúng

    Khi xe dừng hẳn thì vận tốc bằng 0m/s.

    Khi xe dừng hẳn thì v(t) = 0m/s nên 0 = - 5t + 20 \Leftrightarrow t = 4s.

    Nguyên hàm của hàm số vận tốc \int_{}^{}{( - 5t + 20)dt = \frac{- 5t^{2}}{2} + 20t + C}, C\mathbb{\in R}.

    Quãng đường từ lúc đạ phanh cho đến khi xe dừng hẳn là

    \int_{0}^{4}{( - 5t + 20)dt} = \left. \ \left( \frac{- 5t^{2}}{2} + 20t ight) ight|_{0}^{4} = 40m.

  • Câu 6: Nhận biết

    Chọn đáp án đúng

    Hàm số f(x) có nguyên hàm trên K nếu:

    Hàm số f(x) có nguyên hàm trên K nếu f(x) liên tục trên K.

  • Câu 7: Thông hiểu

    Tính vận tốc của khinh khí cầu

    Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162m so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật v(t) = 10t - t^{2}, trong đó t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được tính theo đơn vị mét/phút (m/p). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là:

    Khi bắt đầu tiếp đất vật chuyển động được quãng đường làs = 162m

    Ta có: S = \int_{0}^{t_{0}}{\left( 10t - t^{2} ight)dt} = \left. \ \left( 5t - \frac{t^{3}}{3} ight) ight|_{0}^{t_{0}} = 5{t_{0}}^{2} - \frac{{t_{0}}^{3}}{3} (với t_{0} là thời điểm vật tiếp đất)

    Cho 5{t_{0}}^{2} - \frac{{t_{0}}^{3}}{3} = 162 \Leftrightarrow t_{0} = 9 (Do v(t) = 10t - t^{2} \Rightarrow 0 \leq t \leq 10)

    Khi đó vận tốc của vật là: v(9) = 10.9 - 9^{2} = 9(m/p).

  • Câu 8: Nhận biết

    Tính tích phân

    Giá trị của tích phân \int_{- 1}^{0}{e^{x + 1}dx} bằng:

    Ta có: \int_{- 1}^{0}{e^{x + 1}dx} = \left. \ e^{x + 1} ight|_{- 1}^{0} = e^{1} - e^{0} = e - 1.

  • Câu 9: Thông hiểu

    Tính giá trị biểu thức

    Cho \int_{}^{}{\frac{1}{x^{2} - 1}dx} = a\ln|x - 1| + b\ln|x + 1| + C với a;b là các số hữu tỉ. Khi đó a - b bằng:

    Ta có: \frac{1}{x^{2} - 1} = \frac{1}{(x - 1)(x + 1)} = \frac{1}{x - 1} - \frac{1}{x + 1}

    \Rightarrow \int_{}^{}{\frac{1}{x^{2} - 1}dx} = \int_{}^{}{\left( \frac{1}{x - 1} - \frac{1}{x + 1} ight)dx} = \frac{1}{2}\ln|x - 1| - \frac{1}{2}\ln|x + 1| + C

    Suy ra a = \frac{1}{2};b = - \frac{1}{2} \Rightarrow a - b = 1.

  • Câu 10: Vận dụng cao

    Tính tích phân I

    Tích phân I = \int_{0}^{\frac{\pi}{4}}{\frac{1}{9cos^{2}x - sin^{2}x}dx} có giá trị là:

    Tích phân I = \int_{0}^{\frac{\pi}{4}}{\frac{1}{9cos^{2}x - sin^{2}x}dx} có giá trị là:

    Ta biến đổi: I = \int_{0}^{\frac{\pi}{4}}{\frac{1}{9cos^{2}x - sin^{2}x}dx} = \int_{0}^{\frac{\pi}{4}}{\frac{1}{cos^{2}x\left( 9 - tan^{2}x ight)}dx}.

    Nhận thấy:\left( \tan x ight)' = \frac{1}{cos^{2}x}. Ta dùng đổi biến số.

    Đặt t = \tan x \Rightarrow dt = \frac{1}{cos^{2}x}dx.

    Đổi cận\left\{ \begin{matrix} x = 0 \Rightarrow t = 0 \\ x = \frac{\pi}{4} \Rightarrow t = 1 \\ \end{matrix} ight..

    I = \int_{0}^{1}{\frac{1}{9 - t^{2}}dt} = \frac{1}{6}\int_{0}^{1}{\left( \frac{1}{3 - t} + \frac{1}{3 + t} ight)dt}

    = \left. \ \left( \frac{1}{6}\ln\left| \frac{3 + t}{3 - t} ight| ight) ight|_{0}^{1} = \frac{1}{6}ln2.

    Đáp án đúng là I = \frac{1}{6}\ln 2.

  • Câu 11: Thông hiểu

    Tính diện tích hình phẳng

    Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x^{3} - x và đồ thị hàm số y = x - x^{2}?

    Phương trình hoành độ giao điểm x^{3} - x = x - x^{2} \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 0 \\ x = 2 \\ \end{matrix} ight.

    Khi đó ta có:

    S = \int_{- 2}^{1}{\left| x^{3} + x^{2} - 2x ight|dx}

    = \int_{- 2}^{0}{\left| x^{3} + x^{2} - 2x ight|dx} + \int_{0}^{1}{\left| x^{3} + x^{2} - 2x ight|dx}

    = \left| \int_{- 2}^{0}{\left( x^{3} + x^{2} - 2x ight)dx} ight| + \left| \int_{0}^{1}{\left( x^{3} + x^{2} - 2x ight)dx} ight|

    = \left| \left. \ \left( \frac{x^{4}}{4} + \frac{x^{3}}{3} - x^{2} ight) ight|_{- 2}^{0} ight| + \left| \left. \ \left( \frac{x^{4}}{4} + \frac{x^{3}}{3} - x^{2} ight) ight|_{0}^{1} ight|

    = \frac{8}{3} + \frac{5}{12} = \frac{37}{12}

  • Câu 12: Nhận biết

    Xác định thể tích khối tròn xoay

    Cho hình (H) giới hạn bởi các đường y = - x^{2} + 2x, trục hoành. Quay hình phẳng (H) quanh trục Ox ta được khối tròn xoay có thể tích là:

    Phương trình hoành độ giao điểm của (H);Ox là: - x^{2} + 2x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.

    Khi đó V = \pi\int_{0}^{2}{\left( - x^{2} + 2x ight)^{2}dx} = \pi\int_{0}^{2}{\left( x^{4} - 4x^{3} + 4x^{2} ight)dx} = \frac{16\pi}{15}.

  • Câu 13: Thông hiểu

    Xác định giá trị nguyên của tham số a

    Tích phân I = \int_{1}^{2}\frac{ax - 2}{\sqrt{ax^{2} - 4x}}dx = 2\sqrt{3} - 1. Giá trị nguyên của a là:

    Ta có: \left( ax^{2} - 4x ight)' = 2ax - 4 = 2(ax - 2).

    \Rightarrow I = \frac{1}{2}\int_{1}^{2}\frac{2ax - 4}{\sqrt{ax^{2} - 4x}}dx.

    Đặt t = ax^{2} - 4x \Rightarrow dt = (2ax - 4)dx.

    Đổi cận \left\{ \begin{matrix} x = 2 \Rightarrow t = 4a - 8 \\ x = 1 \Rightarrow t = a - 4 \\ \end{matrix} ight..

    Ta có:

    I = \frac{1}{2}\int_{a - 4}^{4a - 8}\frac{1}{\sqrt{t}}dt = \left. \ \left( \sqrt{t} ight) ight|_{a - 4}^{4a - 8} = \sqrt{4a - 8} - \sqrt{a - 4}

    Theo đề bài:

    I = 2\sqrt{3} - 1 \Leftrightarrow \sqrt{4a - 8} - \sqrt{a - 4} = 2\sqrt{3} - 1

    \Leftrightarrow ..... \Leftrightarrow a = 5.

  • Câu 14: Nhận biết

    Chọn đáp án đúng

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack a;bbrack. Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a;x = b;(a < b) được tính theo công thức

    Theo lí thuyết về tính diện tích hình phẳng ta có diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a;x = b;(a < b) được tính theo công thức: S = \int_{a}^{b}{\left| f(x) ight|dx}.

  • Câu 15: Thông hiểu

    Chọn đáp án đúng

    Tìm một nguyên hàm F(x) của hàm số f(x) = ax + \frac{b}{x^{2}};(x eq 0), biết rằng F( - 1) = 1;F(1) = 4;f(1) = 0?

    Ta có: F(x) = \int_{}^{}{\left( ax + \frac{b}{x^{2}} ight)dx = \frac{ax^{2}}{2} - \frac{b}{x} + c}

    Theo bài ra ta có:

    F( - 1) = 1;F(1) = 4;f(1) = 0

    \Rightarrow \left\{ \begin{matrix}\dfrac{a}{2} + b + c = 1 \\\dfrac{a}{2} - b + c = 4 \\a + b = 0 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}a = \dfrac{3}{2} \\b = - \dfrac{3}{2} \\c = \dfrac{7}{4} \\\end{matrix} ight.. Vậy F(x) = \frac{3x^{2}}{4} + \frac{3}{2x} + \frac{7}{4}.

  • Câu 16: Nhận biết

    Chọn kết luận đúng

    Họ tất cả các nguyên hàm của f(x) = x^{2} + sin2x là

    Ta có \int_{}^{}{f(x)dx} = \int_{}^{}{\left( x^{2} + sin2x \right)dx} = \frac{x^{3}}{3} - \frac{1}{2}cos2x + C.

  • Câu 17: Vận dụng

    Tính tổng các nghiệm của phương trình

    Tìm tổng các nghiệm của phương trình F(x) = x, biết F(x) là một nguyên hàm của hàm số f\left( x ight) = \frac{x}{{\sqrt {8 - {x^2}} }} thỏa mãn F(2) = 0 

    \begin{matrix} F\left( x ight) = \int {f\left( x ight)dx} \hfill \\ = \int {\dfrac{x}{{\sqrt {8 - {x^2}} }}dx} = \dfrac{1}{2}\int {d\frac{x}{{\sqrt {8 - {x^2}} }}d\left( {8 - {x^2}} ight)} \hfill \\ \Rightarrow F\left( x ight) = - \sqrt {8 - {x^2}} + C \hfill \\ \end{matrix}

    Ta có: F(2) = 0 => C = 2

    => F\left( x ight) = - \sqrt {8 - {x^2}} + 2

    Xét phương trình F(x) = x ta có:

    \begin{matrix} F\left( x ight) = x \hfill \\ \Leftrightarrow - \sqrt {8 - {x^2}} + 2 = x \hfill \\ \Leftrightarrow \sqrt {8 - {x^2}} = 2 - x \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2 - x \geqslant 0} \\ {8 - {x^2} = {{\left( {2 - x} ight)}^2}} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 2} \\ {{x^2} - 2x + 2 = 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \leqslant 2} \\ {x = 1 \pm \sqrt 3 } \end{array}} ight. \Leftrightarrow x = 1 - \sqrt 3 \hfill \\ \end{matrix}

    Vậy tổng các nghiệm của phương trình đã cho bằng x = 1 - \sqrt 3

  • Câu 18: Vận dụng cao

    Ghi đáp án vào ô trống

    Cho hình phẳng (H) giới hạn bởi các đường y = \left| x^{2} - 1 ight| và y = k, với 0 < k < 1. Tìm k để diện tích hình phẳng (H) gấp hai lần diện tích hình phẳng được kẻ sọc ở hình vẽ bên (Kết quả được làm tròn đến hàng phần trăm)

    Đáp án: 0,59

    Đáp án là:

    Cho hình phẳng (H) giới hạn bởi các đường y = \left| x^{2} - 1 ight| và y = k, với 0 < k < 1. Tìm k để diện tích hình phẳng (H) gấp hai lần diện tích hình phẳng được kẻ sọc ở hình vẽ bên (Kết quả được làm tròn đến hàng phần trăm)

    Đáp án: 0,59

    Gọi S là diện tích hình phẳng (H). Lúc dó S = 2S_{1} + 2S_{2}, trong đó S_{1} là diện tích phần gạch sọc ở bên phải Oy và S_{2} là diện tích phần gạch ca rô trong hình vẽ bên.

    GọiA,B là các giao diếm có hoành độ dương của đường thẳng y = k và đồ thị hàm sốy = \left| x^{2} - 1 ight|, trong đó A\left( \sqrt{1 - k};k ight) và B\left( \sqrt{1 + k};k ight).

    Thco yêu cầu bài toán S = 2 \cdot 2S_{1} \Leftrightarrow S_{1} = S_{2}.

    \Leftrightarrow \int_{0}^{\sqrt{1 - k}}{\left( 1 - x^{2} - k ight)dx}\ = \int_{\sqrt{1 - k}}^{1}{\left( k - 1 + x^{2} ight)dx} + \int_{1}^{\sqrt{1 + k}}{\left( k - x^{2} + 1 ight)dx}.

    \Leftrightarrow \ (1 - k)\sqrt{1 - k} - \frac{1}{3}(1 - k)\sqrt{1 - k}

    = \frac{1}{3} - (1 - k) - \frac{1}{3}(1 - k)\sqrt{1 - k} + (1 - k)\sqrt{1 - k}

    \ + (1 + k)\sqrt{1 + k} - \frac{1}{3}(1 + k)\sqrt{1 + k} - (1 + k) + \frac{1}{3}

    \Leftrightarrow \ \frac{2}{3}(1 + k)\sqrt{1 + k} = \frac{4}{3}

    \Leftrightarrow \left( \sqrt{1 + k} ight)^{3} = 2 \Leftrightarrow k = \sqrt[3]{4} - 1 \approx 0,59.

  • Câu 19: Thông hiểu

    Tính giá trị của biểu thức

    Cho \int_{0}^{\frac{\pi}{2}}{f(x)dx = 6}. Tính I =\int_{0}^{\frac{\pi}{2}}{\lbrack 3f(x) - 2sinxbrack dx}.

    Ta có:

    I = \int_{0}^{\frac{\pi}{2}}{\lbrack 3f(x) - 2sinxbrack dx}

    = 3\int_{0}^{\frac{\pi}{2}}{f(x)dx} - 2\int_{0}^{\frac{\pi}{2}}{\sin xdx} = 3.6 - 2 = 16.

  • Câu 20: Thông hiểu

    Tính diện tích hình phẳng

    Cho đồ thị hàm số y = f(x) như hình vẽ và \int_{- 2}^{0}{f(x)dx} = a;\int_{0}^{3}{f(x)dx} = b.

    Tính diện tích của phần được gạch chéo theo a;b.

    Từ đồ thị ta suy ra \left\{ \begin{matrix} f(x) \geq 0;\forall x \in \lbrack - 2;0brack \\ f(x) \leq 0;\forall x \in \lbrack 0;3brack \\ \end{matrix} ight.

    Do đó, diện tích phần gạch chéo là

    S = \int_{- 2}^{0}{\left| f(x) ight|dx} + \int_{0}^{3}{\left| f(x) ight|dx}

    = \int_{- 2}^{0}{f(x)dx} - \int_{0}^{3}{f(x)dx} = a - b.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân Cánh Diều Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
122 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 15 phút Chương 4 Nguyên hàm Tích phân Cánh Diều
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 12 - Cánh diều
Xem thêm