Tính P(B|A)
Cho hai biến cố ![]() và
và ![]() , với
, với ![]() ,
, ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Ta có: .
Công thức Bayes:
.
Trong chương trình Toán 12 Cánh Diều, Chương 6: Một số yếu tố xác suất là phần kiến thức quan trọng, thường xuyên xuất hiện trong các đề kiểm tra và đề thi. Đây là chuyên đề giúp học sinh rèn luyện khả năng tư duy xác suất, biết cách phân tích tình huống, xử lý dữ liệu và áp dụng công thức phù hợp. Bài viết này cung cấp đề kiểm tra 45 phút Toán 12 Chương 6 bám sát nội dung SGK, giúp học sinh hệ thống kiến thức, luyện tập kỹ năng giải toán và tự tin chuẩn bị cho các kỳ kiểm tra 1 tiết cũng như ôn tập thi tốt nghiệp.
Tính P(B|A)
Cho hai biến cố ![]() và
và ![]() , với
, với ![]() ,
, ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Ta có: .
Công thức Bayes:
.
Chọn đáp án đúng
Một nhóm học sinh có 20 học sinh, trong đó có 12 em thích học môn Toán, 10 em thích học môn Văn, 2 em không thích học cả hai môn Toán và Văn. Chọn ngẫu nhiên 1 học sinh, xác xuất để học sinh đó thích học môn Toán biết rằng học sinh đó thích học môn Văn là
Gọi là biến cố “học sinh đó thích học môn Toán”,
là biến cố “học sinh đó thích học môn Văn”
Xác suất để học sinh được chọn thích học môn Toán, biết học sinh đó thích học môn Văn chính là .
Ta có ,
,
Ta có
Xác định tính đúng sai của từng phương án
Một chiếc hộp có ![]() viên bi, trong đó có
viên bi, trong đó có ![]() viên bi có tô màu và
viên bi có tô màu và ![]() viên bi không tô màu; các viên bi có kích thước và khối lượng như nhau. Bạn Nam lấy ra viên bi đầu tiên, sau đó bạn Việt lấy ra viên bi thứ hai.
viên bi không tô màu; các viên bi có kích thước và khối lượng như nhau. Bạn Nam lấy ra viên bi đầu tiên, sau đó bạn Việt lấy ra viên bi thứ hai.
a) Xác suất để bạn Nam lấy ra viên bi có tô màu là ![]() . Đúng||Sai
. Đúng||Sai
b) Sơ đồ cây biểu thị tình huống trên là.  Đúng||Sai
Đúng||Sai
c) Xác suất để bạn Việt lấy ra viên bi có tô màu là: ![]() Đúng||Sai
Đúng||Sai
d) Xác suất để bạn Việt lấy ra viên bi không có tô màu là: ![]() . Đúng||Sai
. Đúng||Sai
Một chiếc hộp có ![]() viên bi, trong đó có
viên bi, trong đó có ![]() viên bi có tô màu và
viên bi có tô màu và ![]() viên bi không tô màu; các viên bi có kích thước và khối lượng như nhau. Bạn Nam lấy ra viên bi đầu tiên, sau đó bạn Việt lấy ra viên bi thứ hai.
viên bi không tô màu; các viên bi có kích thước và khối lượng như nhau. Bạn Nam lấy ra viên bi đầu tiên, sau đó bạn Việt lấy ra viên bi thứ hai.
a) Xác suất để bạn Nam lấy ra viên bi có tô màu là ![]() . Đúng||Sai
. Đúng||Sai
b) Sơ đồ cây biểu thị tình huống trên là.  Đúng||Sai
Đúng||Sai
c) Xác suất để bạn Việt lấy ra viên bi có tô màu là: ![]() Đúng||Sai
Đúng||Sai
d) Xác suất để bạn Việt lấy ra viên bi không có tô màu là: ![]() . Đúng||Sai
. Đúng||Sai
Gọi A là biến cố “bạn Việt lấy ra viên bi có tô màu”
Gọi B là biến cố “bạn Nam lấy ra viên bi có tô màu”, suy ra B là biến cố “bạn Việt lấy ra viên bi không có tô màu”.
a) Xác suất để bạn Nam lấy ra viên bi có tô màu là .
b) Ta có:
Sơ đồ cây cần tìm là:
c) Xác suất để bạn Việt lấy ra viên bi có tô màu là:
d) A là biến cố “bạn Việt lấy ra viên bi có tô màu” suy ra A là biến cố “bạn Việt lấy ra viên bi không có tô màu”
Chọn đáp án đúng
Một loại linh kiện do 3 nhà máy số I, số II, số III cùng sản xuất. Tỷ lệ phế phẩm của các nhà máy lần lượt là: I; 0,04; II: 0,03 và III: 0,05. Trong 1 lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I, 120 của nhà máy số II và 100 của nhà máy số III. Khách hàng lấy phải một linh kiện loại phế phẩm từ lô hàng đó. Khả năng linh kiện đó do nhà máy nào sản xuất là cao nhất?
Gọi E1 là biến cố phế phẩm máy số I
E2 là biến cố phế phẩm máy số II
E3 là biến cố phế phẩm máy số III
Gọi B là biến cố khách hàng lấy được 1 linh kiện tốt
Xác suất để khách hàng lấy được linh kiện tốt là:
Gọi là biến cố khách hàng lấy 1 linh kiện loại không tốt
Ta xác định được:
Vậy linh kiện đó do máy III là cao nhất.
Chọn công thức đúng
Cho hai biến cố ![]() và
và ![]() là hai biến cố ngẫu nhiên mà
là hai biến cố ngẫu nhiên mà![]() ,
,![]() , công thức Bayes là:
, công thức Bayes là:
Ta có: .
Chọn đáp án chính xác
Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu? (Làm tròn đến hàng phần trăm).
: "học sinh đã làm đúng bài toán đầu tiên"
.
: "học sinh đã làm đúng bài toán thứ hai"
.
: "học sinh làm đúng cả hai bài toán"
.
Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là
.
Chọn đáp án đúng
Trong học kỳ I năm học 2024 - 2025, sinh viên phải thi 4 học phần. Xác suất để sinh viên thi đạt một học phần trong mỗi lần thi đều là 0,8. Nếu thi không đạt học phần nào phải thi lại học phần đó. Tính xác suất để một sinh viên thi đạt cả 4 học phần trong đó không có học phần nào thi quá 2 lần.
Gọi là "đạt
học phần ở lần thi đầu".
Khi đó, tạo thành hệ đầy đủ và
Gọi là "đạt cả 4 học phần trong đó không có học phần nào thi quá 2 lần".
Áp dụng công thức xác suất toàn phần ta có:
Tính P(A)
Cho hai biến cố ![]() với
với ![]() ,
, ![]() và
và ![]() . Khi đó
. Khi đó ![]() bằng
bằng
Ta có: .
Theo công thức xác suất toàn phần:
.
Chọn đáp án đúng
Người ta điều tra thấy ở một địa phương nọ có ![]() tài xế sử dụng điện thoại di động khi lái xe. Người ta nhận thấy khi tài xế lái xe gây ra tai nạn thì có
tài xế sử dụng điện thoại di động khi lái xe. Người ta nhận thấy khi tài xế lái xe gây ra tai nạn thì có ![]() là do tài xế sử dụng điện thoại. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
là do tài xế sử dụng điện thoại. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
Ta gọi là biến cố “Tài xế sử dụng điện thoại di động khi lái xe”,
là biến cố “Tài xế lái xe gây tai nạn”.
Khi đó
Theo công thức Bayes:
Vậy việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên lần.
Chọn phương án gần đúng với đáp án
Phòng thi đánh giá năng lực có 10 học sinh trong đó có 2 học sinh giỏi (trả lời 100% các câu hỏi), 3 học sinh khá (trả lời 80% các câu hỏi), 5 học sinh trung bình (trả lời 50% các câu hỏi). Gọi ngẫu nhiên một học sinh vào thi và phát đề có 4 câu hỏi (được lấy ngẫu nhiên từ 20 câu). Thấy học sinh này trả lời được cả 4 câu, tính xác suất để học sinh đó là học sinh khá? Xác suất gần bằng số nào sau đây?
Gọi lần lượt là các biến cố gọi một học sinh Giỏi, Khá, Trung Bình
Nên là hệ biến cố đầy đủ.
Gọi B “học sinh đó trả lời được 4 câu hỏi”
Ta có:
Ta lại có:
2 học sinh Giỏi (trả lời 100% các câu hỏi) ⇒ Trả lời 20 câu hỏi
3 học sinh Khá (trả lời 80% các câu hỏi) ⇒ Trả lời câu hỏi.
5 học sinh Trung Bình (trả lời 50% các câu hỏi) ⇒ Trả lời câu hỏi.
Từ đó:
Áp dụng công thức xác suất toàn phần:
Xác suất để sinh viên đó là sinh viên khá là
Áp dụng công thức Bayes ta có:
Chọn đáp án đúng
Một công ty xây dựng đấu thầu 2 dự án độc lập. Khả năng thắng thầu của các dự án 1 là ![]() và dự án 2 là
và dự án 2 là ![]() . Xác suất công ty thắng thầu đúng 1 dự án là:
. Xác suất công ty thắng thầu đúng 1 dự án là:
Gọi A là biến cố ”Thắng thầu dự án 1″
Gọi B là biến cố “Thắng thầu dự án 2″
Theo đề bài ta có: với 2 biến cố
độc lập.
Gọi C là biến cố “Thắng thầu đúng 1 dự án” khi đó ta có:
Tính xác suất P
Giả sử tỉ lệ người dân của tỉnh T nghiện thuốc lá là ![]() ; tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là
; tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là ![]() , trong số người không nghiện thuốc lá là
, trong số người không nghiện thuốc lá là ![]() . Tính xác suất mà người đó là nghiện thuốc lá khi biết bị bệnh phổi?
. Tính xác suất mà người đó là nghiện thuốc lá khi biết bị bệnh phổi?
Gọi A là biến cố “người nghiện thuốc lá”, suy ra A là biến cố “người không nghiện thuốc lá”
Gọi B là biến cố “người bị bệnh phổi”
Để người mà ta gặp bị bệnh phổi thì người đó nghiện thuốc lá hoặc không nghiện thuốc lá.
Ta cần tính
Ta có:
Áp dụng công thức xác suất toàn phần ta có:
Xác suất mà người đó là nghiện thuốc lá khi biết bị bệnh phổi là
Theo công thức Bayes, ta có:
.
Như vậy trong số người bị bệnh phổi của tỉnh T có khoảng số người nghiện thuốc lá.
Tìm xác suất để bi lấy ra màu trắng
Có 3 hộp đựng bi giống nhau, mỗi hộp đựng 5 bi trắng và 7 bi đỏ có cùng kích thước, và trọng lượng. Lần thứ nhất lấy 1 bi từ hộp I bỏ sang hộp II, lần thứ hai lấy 1 từ hộp II bỏ sang hộp III. Cuối cùng lấy 1 bi từ hộp III ra ngoài. Tính xác suất để bi lấy ra đó là bi trắng. (làm tròn kết quả đến hàng phần trăm)
Gọi là biến cố bi lấy ra từ hộp thứ i (
) là bi trắng.
Ta thấy là họ đầy đủ.
Nên ta có xác suất toàn phần
(*)
Lại có là họ đầy đủ.
Nên ta có xác suất toàn phần:
Khi đó
Do đó từ (*) ta có
Chọn công thức đúng
Nếu ![]() là hai biến cố bất kì thì
là hai biến cố bất kì thì
Công thức cần tìm là:
Xác định giá trị P(A)
Cho hai biến cố ![]() và
và ![]() với
với ![]() ,
, ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Ta có .
Công thức xác suất toàn phần:
.
Tính P(A|B)
Cho hai biến cố ![]() và
và ![]() là hai biến cố độc lập, với
là hai biến cố độc lập, với ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Ta có: và
là hai biến cố độc lập nên:
Chọn đáp án đúng
Có 6 khẩu súng cũ và 4 khẩu súng mới, trong đó xác suất trúng khi bắn bằng súng cũ là ![]() , còn súng mới là
, còn súng mới là ![]() . Thực hiện bắn bằng một khẩu súng vào một mục tiêu thì thấy trúng. Hỏi sử dụng loại súng nào khả năng bắn trúng cao hơn?
. Thực hiện bắn bằng một khẩu súng vào một mục tiêu thì thấy trúng. Hỏi sử dụng loại súng nào khả năng bắn trúng cao hơn?
Gọi M là biến cố "bắn bằng khẩu mới" thì là biến cố "bắn bằng khẩu cũ".
Có P(M) = 0,4 và P( ) = 0,6.
Gọi T là biến cố "bắn trúng" thì theo đề bài, ta có:
P(T | M) = 0,95; P(T | ) = 0,8.
Áp dụng công thức xác suất điều kiện suy ra
Suy ra bắn bằng khẩu cũ có khả năng xảy ra cao hơn.
Tính P(A|B)
Cho hai biến cố ![]() và
và ![]() , với
, với ![]() ,
, ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Ta có:
Chọn mệnh đề đúng
Cho hai biến cố ![]() và
và ![]() . Chọn mệnh đề đúng?
. Chọn mệnh đề đúng?
Ta có: .
Tính P(A|B)
Cho hai biến cố ![]() và
và ![]() là hai biến cố độc lập, với
là hai biến cố độc lập, với ![]() ;
; ![]() .
.
Tính ![]() .
.
Ta có: và
là hai biến cố độc lập nên:
Tính xác suất P
Trước khi đưa sản phẩm ra thị trường người ta đã phỏng vấn ngẫu nhiên 200 khách hàng về sản phẩm đó và thấy có 34 người tả lời “sẽ mua”, 97 người trả lời “có thể sẽ mua” và 69 người trả lời “không mua”. Kinh nghiệm cho thấy tỷ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời trên tương ứng là 70%, 30% và 1%. Trong số khách hàng thực sự mua sản phẩm thì có bao nhiêu phần trăm trả lời “sẽ mua”?
Gọi H1, H2, H3 lần lượt là 3 biến cố tương ứng với 3 cách trả lời của khách hàng được phỏng vấn:
H1 – người đó trả lời “sẽ mua”
H2 – người đó trả lời “có thể mua”
H3 – người đó trả lời “không mua”
H1, H2, H3 là một hệ đầy đủ các biến cố với xác suất tương ứng
Ta xác định được:
Theo công thức xác suất đầy đủ ta có:
.
Theo công thức Bayes:
.
Tính xác suất để Hà được chọn vào đội tuyển
Để được chọn vào đội tuyển học sinh giỏi môn Toán cấp thành phố, mỗi thí sinh phải vượt qua hai vòng thi. Bạn Hà tham dự cuộc tuyển chọn này. Xác suất để Hà qua được vòng thứ nhất là ![]() . Nếu qua được vòng thứ nhất thì xác suất để Hà qua được vòng thứ hai là
. Nếu qua được vòng thứ nhất thì xác suất để Hà qua được vòng thứ hai là ![]() . Xác suất để bạn Hà được chọn vào đội tuyển này là
. Xác suất để bạn Hà được chọn vào đội tuyển này là
Gọi là biến cố: “Hà qua được vòng thứ nhất” và
là biến cố: “Hà qua được vòng thứ hai”. Khi đó biến cố: “Hà được chọn vào đội tuyển” là
.
Ta có .
Tính xác suất cỉa biến cố A
Cho hai biến cố ![]() và
và ![]() biết
biết ![]() . Tính
. Tính ![]()
Ta có:
Tìm giá trị xác suất
Cho hai biến cố ![]() và
và ![]() , với
, với ![]() . Tính
. Tính ![]() ?
?
Ta có:
.
Ghi đáp án vào ô trống
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là ![]() và khả năng thắng thầu của dự án 2 là
và khả năng thắng thầu của dự án 2 là ![]() . Khả năng thắng thầu cả 2 dự án là
. Khả năng thắng thầu cả 2 dự án là ![]() . Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là
. Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là ![]() . Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là
. Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là ![]() . Khi đó biểu thức
. Khi đó biểu thức ![]() là bao nhiêu?
là bao nhiêu?
Đáp án: 4
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là ![]() và khả năng thắng thầu của dự án 2 là
và khả năng thắng thầu của dự án 2 là ![]() . Khả năng thắng thầu cả 2 dự án là
. Khả năng thắng thầu cả 2 dự án là ![]() . Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là
. Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là ![]() . Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là
. Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là ![]() . Khi đó biểu thức
. Khi đó biểu thức ![]() là bao nhiêu?
là bao nhiêu?
Đáp án: 4
Gọi là biến cố: “Thắng thầu dự án 1”
Gọi là biến cố: “Thắng thầu dự án 2”.
Theo giả thiết suy ra: ;
và
Gọi là biến cố: “Thắng thầu dự án 2 biết công ty thắng thầu dự án 1”
Khi đó:
Gọi là biến cố: “Thắng thầu dự án 2 biết công ty không thắng thầu dự án 1”
Khi đó:
Vậy .
Ghi đáp án đúng vào ô trống
Một địa phương có tỉ lệ người dân nghiện thuốc lá là ![]() . Biết rằng tỉ lệ người bị viêm họng trong số người nghiện thuốc lá là
. Biết rằng tỉ lệ người bị viêm họng trong số người nghiện thuốc lá là ![]() , còn tỉ lệ đó trong số người không nghiện thuốc lá là
, còn tỉ lệ đó trong số người không nghiện thuốc lá là ![]() . Chọn ngẫu nhiên một người bị viêm họng từ địa phương trên. Tính xác suất để người đó nghiện thuốc lá, kết quả làm tròn đến hàng phần trăm
. Chọn ngẫu nhiên một người bị viêm họng từ địa phương trên. Tính xác suất để người đó nghiện thuốc lá, kết quả làm tròn đến hàng phần trăm
Đáp án: 0,39||0.39
Một địa phương có tỉ lệ người dân nghiện thuốc lá là ![]() . Biết rằng tỉ lệ người bị viêm họng trong số người nghiện thuốc lá là
. Biết rằng tỉ lệ người bị viêm họng trong số người nghiện thuốc lá là ![]() , còn tỉ lệ đó trong số người không nghiện thuốc lá là
, còn tỉ lệ đó trong số người không nghiện thuốc lá là ![]() . Chọn ngẫu nhiên một người bị viêm họng từ địa phương trên. Tính xác suất để người đó nghiện thuốc lá, kết quả làm tròn đến hàng phần trăm
. Chọn ngẫu nhiên một người bị viêm họng từ địa phương trên. Tính xác suất để người đó nghiện thuốc lá, kết quả làm tròn đến hàng phần trăm
Đáp án: 0,39||0.39
Đặt
Biến cố : "người dân nghiện thuốc lá"
Biến cố B : "người dân bị viêm họng"
Khi đó:
Trước tiên ta tính xác suất người này viêm họng
.
Xác suất để người nghiện thuốc lá nếu bị viêm họng là
.
Chọn đáp án đúng
Cho hai biến cố ![]() và
và ![]() . Biết
. Biết ![]() ;
; ![]() ;
; ![]() . Khi đó
. Khi đó ![]() bằng
bằng
Ta có: .
Theo công thức xác suất toàn phần, ta có:
.
Tính xác suất lấy hai bi trắng
Một hộp có 4 viên bi, mỗi viên có thể là màu đen hoặc trắng. Lấy ngẫu nhiên ra hai viên bi. Tính xác suất để lấy được hai bi trắng.
Số lượng bi trắng và đen trong hộp chỉ có thể xảy ra 1 trong 5 trường hợp sau:
H4: 4 bi trắng
H3: 3 bi trắng; 1 bi đen
H2: 2 bi trắng; 2 bi đen
H1: 1 bi trắng; 3 bi đen
H0: 0 bi trắng; 4 bi đen
Gọi biến cố A là biến cố lấy được 2 bi trắng
Ta có:
Ghi đáp án vào ô trống
Một bệnh truyền nhiễm có xác suất lây bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Chị Mai có tiếp xúc với người bệnh hai lần, một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất để chị Mai bị lây bệnh từ người bệnh truyền nhiễm đó. (Kết quả ghi dưới dạng số thập phân).
Đáp án: 0,82
Một bệnh truyền nhiễm có xác suất lây bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Chị Mai có tiếp xúc với người bệnh hai lần, một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất để chị Mai bị lây bệnh từ người bệnh truyền nhiễm đó. (Kết quả ghi dưới dạng số thập phân).
Đáp án: 0,82
Gọi là biến cố: "Chị Hoa bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và
: "Chị Hoa bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”.
Dễ thấy là hai biến cố độc lập.
Xác suất để chị Hoa không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là
.
Gọi là xác suất để chị Hoa bị lây bệnh khi tiếp xúc người bệnh, ta có:
Xét tính đúng sai của các phương án
Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là ![]() và dự án 2 là
và dự án 2 là ![]() . Khả năng thắng thầu của 2 dự án là 0,4. Gọi
. Khả năng thắng thầu của 2 dự án là 0,4. Gọi ![]() lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) ![]() là hai biến độc lập. Đúng||Sai
là hai biến độc lập. Đúng||Sai
b) Xác suất công ty thắng thầu đúng 1 dự án là ![]() . Đúng||Sai
. Đúng||Sai
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là ![]() . Sai|| Đúng
. Sai|| Đúng
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án ![]() . Sai|| Đúng
. Sai|| Đúng
Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là ![]() và dự án 2 là
và dự án 2 là ![]() . Khả năng thắng thầu của 2 dự án là 0,4. Gọi
. Khả năng thắng thầu của 2 dự án là 0,4. Gọi ![]() lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) ![]() là hai biến độc lập. Đúng||Sai
là hai biến độc lập. Đúng||Sai
b) Xác suất công ty thắng thầu đúng 1 dự án là ![]() . Đúng||Sai
. Đúng||Sai
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là ![]() . Sai|| Đúng
. Sai|| Đúng
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án ![]() . Sai|| Đúng
. Sai|| Đúng
Ta có:
a) là hai biến cố độc lập khi và chỉ khi
Mà nên
không độc lập.
b) Gọi C là biến cố thắng thầu đúng 1 dự án
.
c) Gọi D là biến cố thắng dự 2 biết thắng dự án 1
.
d) Gọi E là biến cố “thắng dự án 2 biết không thắng dự án 1”
.
Tính xác suất để hai đứa trẻ là con gái
Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu? Cho biết xác suất để một đứa trẻ là trai hoặc gái là bằng nhau.
Giới tính cả 2 đứa trẻ là ngẫu nhiên và không liên quan đến nhau.
Do gia đình có 2 đứa trẻ nên sẽ có thể xảy ra 4 khả năng:
(trai, trai), (gái, gái), (gái, trai), (trai, gái).
Gọi A là biến cố “Cả hai đứa trẻ đều là con gái”
Gọi B là biến cố “Có ít nhất một đứa trẻ là con gái”
Ta có
Do nếu xảy ra A thì đương nhiên sẽ xảy ra B nên ta có:
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là
Tính xác suất bắn trúng
Cuối tuần M đến sân chơi để bắn cung, biết khoảng cách bắn tên thay đổi liên tục và khả năng bạn M bắn trúng bia tỉ lệ nghịch với khoảng cách bắn. M bắn lần đầu ở khoảng cách ![]() với xác suất trúng bia là
với xác suất trúng bia là ![]() , nếu bị trượt M bắn tiếp mũi tên thứ hai ở khoảng cách
, nếu bị trượt M bắn tiếp mũi tên thứ hai ở khoảng cách ![]() , nếu lại trượt M bắn mũi tên thứ ba ở khoảng cách
, nếu lại trượt M bắn mũi tên thứ ba ở khoảng cách ![]() . Tính xác suất để M bắn trúng bia?
. Tính xác suất để M bắn trúng bia?
Gọi A là biến cố “M bắn trúng bia ở lần thứ nhất”
Gọi B là biến cố “M bắn trúng bia ở lần thứ hai”
Gọi C là biến cố “M bắn trúng bia ở lần thứ ba”
Ta có:
Vì xác suất bắn trúng bia trong mỗi lần bắn tỷ lệ nghịch với khoảng cách bắn nên ta có:
Ta có sơ đồ cây như sau:
Xác suất để M bắn trúng bia là:
Tính xác suất theo yêu cầu
Có hai chuồng thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 7 con thỏ đen và 3 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng. (Kết quả làm tròn đến chữ số thập phân thứ 2).
Xét A:“Con thỏ được lấy ra từ chuồng II để cho vào chuồng I là con thỏ trắng”.
Và B: “Con thỏ được lấy ra từ chuồng I là con thỏ trắng”.
Tính P(A): Đây là xác suất để lấy ra ngẫu nhiên 1 con thỏ trắng từ chuồng II rồi cho vào chuồng I:
Tính : Đây là xác suất để lấy ra ngẫu nhiên 1 con thỏ trắng từ chuồng I với điều kiện đã chọn ra 1 con thỏ trắng từ chuồng II rồi cho vào chuồng I.
Tức là có 5 con thỏ đen và 11 con thỏ trắng ở trong chuồng I
Tương tự ta có:
Tính : Đây là để lấy ra ngẫu nhiên 1 con thỏ trắng từ chuồng I với điều kiện đã chọn ra 1 con thỏ đen từ chuồng II rồi cho vào chuồng I
Tức là có 6 con thỏ đen và 10 con thỏ trắng ở trong chuồng I. Tương tự như trên ta có: .
Tính xác suất của biến cố B
Cho sơ đồ hình cây như sau
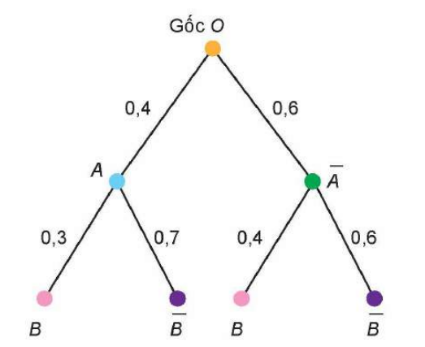
Tính xác suất của biến cố ![]() .
.
Ta có .
Xét tính đúng sai của các phương án
Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 viên bi đỏ và 5 viên bi xanh, hộp thứ hai chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Gọi A là biến cố “Viên bị được lấy ra từ hộp thứ hai là bi đỏ”, B là biến cố “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ”. Các khẳng định sau đúng hay sai?
a) Xác suất của biến cố B là ![]() .Đúng||Sai
.Đúng||Sai
b) Giả sử viên bi lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bị đỏ thì khi đó ![]() . Đúng||Sai
. Đúng||Sai
c) Gọi ![]() : “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” thì
: “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” thì ![]() . Sai||Đúng
. Sai||Đúng
d) Xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ là ![]() . Đúng||Sai
. Đúng||Sai
Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 5 viên bi đỏ và 5 viên bi xanh, hộp thứ hai chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Gọi A là biến cố “Viên bị được lấy ra từ hộp thứ hai là bi đỏ”, B là biến cố “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ”. Các khẳng định sau đúng hay sai?
a) Xác suất của biến cố B là ![]() .Đúng||Sai
.Đúng||Sai
b) Giả sử viên bi lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bị đỏ thì khi đó ![]() . Đúng||Sai
. Đúng||Sai
c) Gọi ![]() : “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” thì
: “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” thì ![]() . Sai||Đúng
. Sai||Đúng
d) Xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ là ![]() . Đúng||Sai
. Đúng||Sai
a) Ta có: B là biến cố “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ” nên .
b) Giả sử viên bi lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bị đỏ thì sau khi chuyển, hộp thứ hai có 7 bi đỏ và 4 bi xanh nên .
c) Gọi : “Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh” Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh thì sau khi chuyển, hộp thứ hai có 6 bi đỏ và 5 bi xanh.
Khi đó .
d) Ta có:
Xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ là:
Áp dụng công thức xác suất toàn phần, ta có:
.
Tìm xác suất có điều kiện
Gieo đồng thời hai con xúc sắc cân đối. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc sắc là ![]() , biết rằng có ít nhất một con xúc sắc xuất hiện mặt
, biết rằng có ít nhất một con xúc sắc xuất hiện mặt ![]() chấm.
chấm.
Gọi là biến cố “Tổng số chấm xuất hiện trên hai con xúc sắc là
” và
là biến cố “Có ít nhất một con xúc sắc xuất hiện mặt
chấm”.
Ta có
;
.
Suy ra .
Xét tính đúng sai của các kết luận
Khi điều tra sức khỏe nhiều người cao tuổi ở một địa phương, người ta thấy rằng có ![]() người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường là
người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường là ![]() trong những người không bị bệnh tiểu đường là
trong những người không bị bệnh tiểu đường là ![]() Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra sức khỏe.
Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra sức khỏe.
a) Xác suất chọn được người bị bệnh tiểu đường là 0,4. Đúng||Sai
b) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó bị bệnh tiểu đường, là 0,7. Đúng||Sai
c) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó không bị bệnh tiểu đường, là 0,75. Sai||Đúng
d) Xác suất chọn được người bị bệnh huyết áp cao là 0,8. Sai||Đúng
Khi điều tra sức khỏe nhiều người cao tuổi ở một địa phương, người ta thấy rằng có ![]() người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường là
người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường là ![]() trong những người không bị bệnh tiểu đường là
trong những người không bị bệnh tiểu đường là ![]() Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra sức khỏe.
Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra sức khỏe.
a) Xác suất chọn được người bị bệnh tiểu đường là 0,4. Đúng||Sai
b) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó bị bệnh tiểu đường, là 0,7. Đúng||Sai
c) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó không bị bệnh tiểu đường, là 0,75. Sai||Đúng
d) Xác suất chọn được người bị bệnh huyết áp cao là 0,8. Sai||Đúng
Xét các biến cố: : “Chọn được người bị bệnh tiểu đường”;
: “Chọn được người bị bệnh huyết áp cao”.
Khi đó,
Theo công thức xác suất toàn phần, ta có:
Đáp án: a) Đ, b) Đ, c) S, d) S.
Tính xác suất có điều kiện
Cho hai biến cố ![]() và
và ![]() là hai biến cố độc lập, với
là hai biến cố độc lập, với ![]() ,
, ![]() . Tính
. Tính ![]() .
.
Theo bài ra ta có:
và
là hai biến cố độc lập nên:
Xác định tính đúng sai của từng phương án
Cho hai biến cố ![]() và
và ![]() là hai biến cố độc lập, với
là hai biến cố độc lập, với ![]() .
.
a) ![]() Sai|| Đúng
Sai|| Đúng
b) ![]() Đúng||Sai
Đúng||Sai
c) ![]() Sai|| Đúng
Sai|| Đúng
d) ![]() Đúng||Sai
Đúng||Sai
Cho hai biến cố ![]() và
và ![]() là hai biến cố độc lập, với
là hai biến cố độc lập, với ![]() .
.
a) ![]() Sai|| Đúng
Sai|| Đúng
b) ![]() Đúng||Sai
Đúng||Sai
c) ![]() Sai|| Đúng
Sai|| Đúng
d) ![]() Đúng||Sai
Đúng||Sai
Ta có:
Do hai biến cố và
là hai biến cố độc lập nên
và
;
và
;
và
độc lập với nhau.
a) và
là hai biến cố độc lập nên:
b) và
là hai biến cố độc lập nên:
c) và
là hai biến cố độc lập nên:
d) và
là hai biến cố độc lập nên:
Xác định công thức đúng
Cho ba biến cố ![]() độc lập từng đôi thỏa mãn
độc lập từng đôi thỏa mãn ![]() và
và ![]() . Xác định
. Xác định ![]() ?
?
Ta có:
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

