Cho hàm số y = f(x) có đạo hàm . Hàm số y = -2f(x) đồng biến trên khoảng
Ta có:
=> Hàm số y = -2f(x) đồng biến trên khoảng (0; 2)
Cho hàm số y = f(x) có đạo hàm . Hàm số y = -2f(x) đồng biến trên khoảng
Ta có:
=> Hàm số y = -2f(x) đồng biến trên khoảng (0; 2)
Gọi M, N lần lượt là số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số . Khi đó m + n bằng:
Điều kiện
Tiệm cận ngang:
=> Đồ thị hàm số có 1 tiệm cận ngang là y = 1
Tiệm cận đứng:
Điều kiện cần: Xét phương trình x2 – 4 = 0 => x = 2 hoặc x = -2
Điều kiện đủ
Đặt
Xét x = 2 ta có f(2) = 0 nên ta sẽ đi tìm bậc của x – 2 của f(x)
=> x = 2 không phải là tiệm cận đứng
Xét x = -2 ta có f(-2) không tồn tại hay x = -2 không phải là tiệm cận đứng.
Vậy M = 1, N = 0 => M + N = 1
Cho hàm số xác định, liên tục trên
và có đồ thị là đường cong như hình vẽ.
Giá trị lớn nhất và giá trị nhỏ nhất
của hàm số
trên
là:
Dựa vào đồ thị .
Cho hàm số . Khẳng định nào sau đây đúng?
Ta có:
Suy ra hàm số nghịch biến trên khoảng
Mà nên hàm số cũng nghịch biến trên khoảng
.
Cho hàm số . Có bao nhiêu giá trị nguyên của tham số
thuộc
để hàm số đã cho đồng biến trên khoảng
.
Ta có đạo hàm của là
.
Hàm số đã cho đồng biến trên khoảng khi và chỉ khi
(*)
Xét hàm số
ta có do đó ta có bảng biến thiên của hàm số
như sau
Qua bảng biến thiên ta có , kết hợp với
ta có 6 giá trị nguyên của
là
.
Cho hàm số có đồ thị như hình vẽ bên. Tiệm cận ngang của đồ thị hàm số là:
Dựa vào đồ thị ta thấy đồ thị có tiệm cận ngang là
Cho hàm số có đồ thị như hình vẽ:
Tìm số điểm cực trị của hàm số trên khoảng
?
Đặt
Từ bảng xét dấu của hàm số có
Ta có bảng biến thiên
Từ bảng biến thiên suy ra hàm số có hai cực trị trên khoảng
.
Tìm tất cả các giá trị của tham số để hàm số
đồng biến trên
?
Ta có:
Hàm số đồng biến trên
Dễ thấy
Vậy hàm số đã cho đồng biến trên khi
.
Một chuyển động thẳng xác định bởi phương trình , trong đó
tính bằng mét và
là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại
.
Vận tốc tức thời của chuyển động là:
Khi
Cho hàm số với
là tham số. Tìm giá trị của
để đường tiệm cận ngang của đồ thị hàm số đi qua điểm
?
Ta có: suy ra
là tiệm cận ngang của đồ thị hàm số đã cho.
Do
Cho hàm số với
là tham số. Xác định điều kiện của tham số
để hàm số đã cho đạt cực đại tại
?
Ta có:
Hàm số đạt cực đại tại suy ra
Với ta có:
suy ra hàm số đạt cực đại tại
.
Với ta có:
suy ra hàm số đạt cực tiểu tại
.
Vậy giá trị của tham số m thỏa mãn yêu cầu là
Điều kiện của tham số để hàm số
nghịch biến trên từng khoảng xác định là:
Xét hàm số ta có:
Tập xác định
Ta có:
Hàm số nghịch biến trên từng khoảng xác định
Vậy đáp án cần tìm là .
Gọi K là tập hợp các giá trị nguyên của tham số để bất phương trình
nghiệm đúng với mọi
. Số các phần tử của tập hợp K là:
Đặt
Bất phương trình đã cho trở thành
Yêu cầu bài toán tương đương với bất phương trình (*) nghiệm đúng với mọi
Xét hàm số
Vì
Do đó bất phương trình (*) nghiệm đúng với mọi khi và chỉ khi
Mặt khác m là số nguyên thuộc [0; 2019] nên
Tập hợp tất cả các giá trị thực của tham số để hàm số
đồng biến trên khoảng
là
Điều kiện .
Ta có
Để hàm số đồng biến trên khoảng
thì
.
Cho hàm số với
là tham số thực và
Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?
Khi thì phương trình
vô nghiệm nên đồ thị hàm số không có tiệm cận đứng.
Ta có là TCN;
là TCN.
Vậy đồ thị hàm số có đúng hai tiệm cận.
Cho hàm số , bảng xét dấu của
như sau:
Hàm số đồng biến trên khoảng nào dưới đây?
Ta có .
.
.
Bảng biến thiên
Dựa vào bảng biến thiên hàm số đồng biến trên khoảng
.
Cho hàm số có đồ thị
. Các mệnh đề sau đúng hay sai?
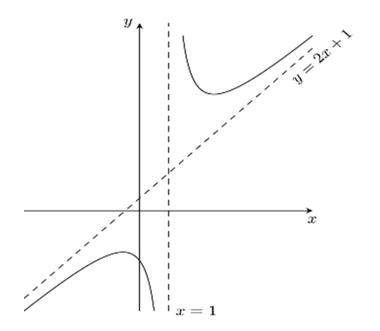
a) Tập xác định của hàm số là . Đúng||Sai
b) Tiệm cận xiên của đồ thị là đường thẳng
. Đúng||Sai
c) Điểm là tâm đối xứng của đồ thị
. Sai||Đúng
Cho hàm số có đồ thị
. Các mệnh đề sau đúng hay sai?

a) Tập xác định của hàm số là . Đúng||Sai
b) Tiệm cận xiên của đồ thị là đường thẳng
. Đúng||Sai
c) Điểm là tâm đối xứng của đồ thị
. Sai||Đúng
a) Tập xác định của hàm số là suy ra mệnh đề đúng.
b) Ta có
Do đó đường thẳng là tiệm cận xiên của đồ thị suy ra mệnh đề đúng.
c) Đồ thị hàm số nhận làm tiệm cận đứng.
Tọa độ giao điểm của hai đường tiệm cận là . Do đó
là tâm đối xứng của
suy ra mệnh đề sai.
Cho hàm số có bảng biến thiên như sau:
Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
Từ bảng biến thiên ta có: .
Cho hàm số có bảng biến thiên như sau:
Số điểm cực trị của đồ thị hàm số là:
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
Số dân của một thị trấn sau năm kể từ năm
được ước tính bởi công thức
được tính bằng nghìn người).

Hỏi trong khoảng thời gian từ năm đến năm
dân số của thị trấn đạt giá trị lớn nhất bằng bao nhiêu?
Xét hàm số với
suy ra
.
Suy ra hàm số đồng biến trên đoạn
.
Vậy dân số đạt giá trị lớn nhất bằng .
Hàm số trên đoạn
có giá trị nhỏ nhất bằng:
Ta có:
. Khi đó
suy ra
.
Hỏi đồ thị hàm số có tất cả bao nhiêu đường tiệm cận?
Tập xác định
Ta có:
Suy ra là tiệm cận ngang của đồ thị hàm số.
Suy ra hàm số không có tiệm cận đứng
Vậy hàm số có 1 đường tiệm cận.
Cho hàm số có hai điểm cực trị
. Tính độ dài đoạn thẳng
?
Ta có:
Nhận thấy phương trình có hai nghiệm phân biệt nên đồ thị hàm số có hai điểm cực trị là
Có tất cả bao nhiêu giá trị nguyên của tham số để hàm số
đồng biến trên tập số thực?
Ta có:
Hàm số đồng biến trên
Vì
Vậy số giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán là .
Cho hàm số có đạo hàm liên tục trên
và có bảng biến thiên của đạo hàm như hình vẽ.
Đặt . Tìm số điểm cực trị của hàm số
Đáp án: 6
Cho hàm số có đạo hàm liên tục trên
và có bảng biến thiên của đạo hàm như hình vẽ.
Đặt . Tìm số điểm cực trị của hàm số
Đáp án: 6
Đặt
Xét hàm số
Bảng biến thiên của hàm số
Dựa vào bảng biến thiến trên ta thấy phương trình .
Mỗi phương trình có hai nghiệm phân biệt khác , mà
có 4 nghiệm đơn phân biệt
khác
và phương trình
vô nghiệm.
Do đó phương trình có 6 nghiệm đơn phân biệt lần lượt theo thứ tự từ nhỏ đến lớn là
.
Vậy hàm số có 6 cực trị.
Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyển động , trong đó
,
là thời gian chuyển động,
là độ cao so với mặt đất. Sau bao lâu kể từ khi bắn thì viên đạn đạt được độ cao
?
Khi viên đạn đạt được độ cao, ta có phương trình:
Vậy sau kể từ khi bắn thì viên đạn đạt được độ cao
.
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao so với bể mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao
của con tàu so với bề mặt của Mặt Trăng được tính (gẩn đúng) bởi hàm
trong đó
là thời gian tính bằng giây và
là độ cao tính bằng kilômét. Gọi
là vận tốc tức thời của con tàu ở thời điểm
(giây) kể từ khi đốt cháy các tên lửa hãm với
. Tại thời điểm
(giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Vận tốc tức thời của con tàu ở thời điểm ,
, là đạo hàm của hàm số
theo thời gian
. Hàm số
đã cho là:
Để tìm , ta lấy đạo hàm của
:
Vậy hàm số biểu diễn vận tốc tức thời của con tàu ở thời điểm
là:
Để xác định liệu vận tốc của con tàu tại thời điểm t = 25 giây có đang tăng hay giảm, chúng ta cần xem xét đạo hàm bậc hai của hàm số , tức là gia tốc của con tàu.
Gia tốc là đạo hàm của vận tốc
tức là đạo hàm bậc hai của
Tại thời điểm giây, gia tốc của con tàu là:
Vi gia tốc , nên vận tốc của con tàu tại thời điểm
giây đang giảm
Số tiệm cận của hàm số là:
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Tập xác định:
Khi đó
=> Đồ thị hàm số có hai tiệm cận ngang
Mặt khác
=> Đồ thị hàm số có hai tiệm cận đứng
Vậy đồ thị hàm số đã cho có 4 đường tiệm cận.
Số các giá trị nguyên của tham số để hàm số
có giá trị nhỏ nhất trên đoạn
thuộc khoảng
là:
Xét hàm số trên
ta có:
Mà
Vậy có tất cả 6 giá trị nguyên của tham số m thỏa mãn yêu cầu.
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
Khi
Suy ra đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng
Khi
Suy ra đồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng
Vậy đồ thị hàm số có tất cả 4 đường tiệm cận.
Hình bên cho biết lượng mưa trung bình các tháng năm 2019 tại Thành phố Hồ Chí Minh đo theo đơn vị milimet. Hãy cho biết vào tháng nào trong năm 2019 thì lượng mưa là cao nhất ?
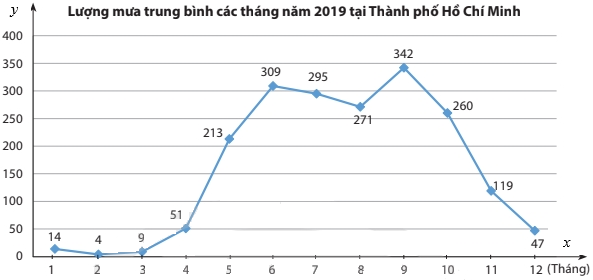
Từ đồ thị ta thấy vào Tháng 9 thì lượng mưa ở Thành phố Hồ Chí Minh cao nhất trong năm 2019
Cho hàm số
Ta có: có hai nghiệm phân biệt là -2 và 3
=> f’(x) < 0 =>
Vậy hàm số nghịch biến trên khoảng (-2; 3)
Gọi A, B, C là các điểm cực trị của đồ thị hàm số . Bán kính của đường tròn nội tiếp tam giác ABC bằng:
Ta có:
=> Đồ thị hàm số có ba điểm cực trị là A(0; 4), B(1; 3), C(-1;; 3)
Tính được
Áp dụng công thức tính bán kính đường tròn nội tiếp tam giác ABC ta có:
Cho hàm số . Tính giá trị nhỏ nhất của hàm số đã cho trên đoạn
?
Hàm số liên tục trên đoạn
Ta có:
Khi đó nên
.
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá đồng một chiếc và mỗi tháng cơ sở bán được trung bình
chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá
đồng mà cứ tăng giá thêm
đồng thì mỗi tháng sẽ bán ít hơn
chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là
.
a) Nếu cơ sở bán mỗi chiếc khăn với giá thì số tiền lãi sau 1 tháng là
. Sai||Đúng
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức
. Đúng||Sai
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm chiếc. Sai||Đúng
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá đồng. Đúng||Sai
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá đồng một chiếc và mỗi tháng cơ sở bán được trung bình
chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá
đồng mà cứ tăng giá thêm
đồng thì mỗi tháng sẽ bán ít hơn
chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là
.
a) Nếu cơ sở bán mỗi chiếc khăn với giá thì số tiền lãi sau 1 tháng là
. Sai||Đúng
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức
. Đúng||Sai
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm chiếc. Sai||Đúng
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá đồng. Đúng||Sai
Gọi số tiền cần tăng giá mỗi chiếc khăn là .
Vì cứ tăng giá thêm thì số khăn bán ra giảm
chiếc nên tăng
thì số khăn bán ra giảm
chiếc.
Do đó tổng số khăn bán ra mỗi tháng là: chiếc.
Lúc đầu bán với giá , mỗi chiếc khăn có lãi
.
Sau khi tăng giá, mỗi chiếc khăn thu được số lãi là: .
Do đó tổng số lợi nhuận một tháng thu được sau khi tăng giá là:
.
Xét hàm số trên
.
Ta có: .
Lập bảng biến thiên của hàm số trên
ta thấy hàm số đạt giá trị lớn nhất khi
Như vậy, để thu được lợi nhuận cao nhất thì cơ sở sản xuất cần tăng giá bán mỗi chiếc khăn là đồng, tức là mỗi chiếc khăn bán với giá mới là
đồng.
Vậy:
a) sai. b) đúng. c) sai. d) đúng.
Hàm số nghịch biến trên khoảng
khi và chỉ khi:
Tập xác định
Ta có:
Hàm số đã cho nghịch biến trên khoảng
khi và chỉ khi
Xét hàm số trên
ta có bảng biến thiên như sau:
Dựa vào bảng biến thiên ta có:
Do đó
Vậy thỏa mãn yêu cầu bài toán.
Cho hàm số f(x) có đạo hàm f’(x). Đồ thị của hàm số y = f’(x) được biểu diễn trong hình vẽ dưới đây.
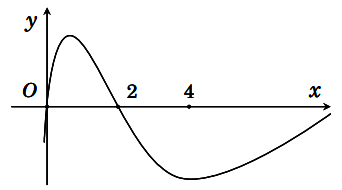
Biết rằng . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f(x) trên đoạn [0; 4]?
Ta có bảng xét dấu như sau:

Dựa vào bảng xét dấy ta có M = f(2), GTNN chỉ có thể là f(0) hoặc f(4)
Ta lại có
f(1) và f(3) nhỏ hơn f(2) => f(1) + f(3) < 2f(2)
=> 2f(2) – f(1) – f(3) > 0
Theo bài ra ta có:
f(0) + f(1) + f(3) = f(4) + 2f(2)
=> f(0) – f(4) = 2f(2) – f(1) – f(3) > 0
=> f(0) – f(4) > 0 => f(0) > f(4)
=> GTNN đạt được tại x = 4
Gọi giá trị nhỏ nhất của hàm số trên đoạn
là
. Chọn khẳng định đúng?
Tập xác định
Ta có:
Suy ra hàm số đồng biến trên suy ra
Mực nước biển trung bình tại trường sa từ năm 2013 đến năm 2019 được cho bởi biểu đồ trong hình bên dưới.
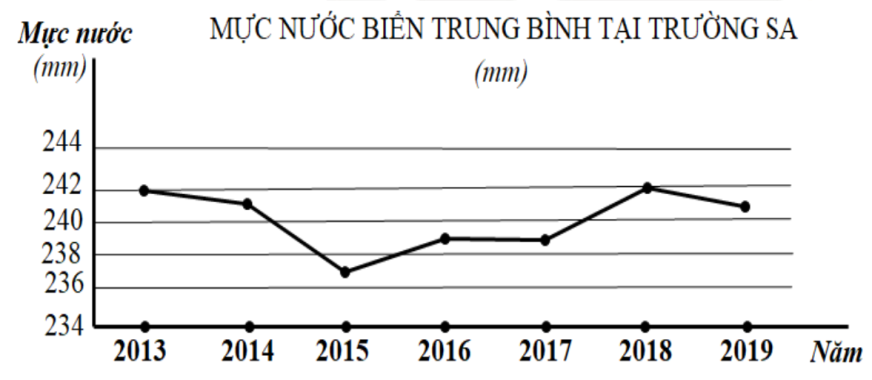
Trong khoảng thời gian từ năm 2016 đến năm 2019, năm nào mực nước biển trung bình tại trường sa cao nhất ?
Nhìn vào biểu đồ ta thấy, tại năm 2018 mực nước biển trung bình tại trường sa cao nhất bằng .
Đường tiệm cận đứng của đồ thị hàm số
Ta có:
và
Do đó đồ thị hàm số có hai đường tiệm cận đứng
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

