Đề thi học kì 2 Toán 10 Cánh Diều (Cấu trúc mới) năm 2025 Đề 4

Đề thi học kì 2 môn Toán 10 Cánh Diều

Đề thi học kì 2 lớp 10 môn Toán Cánh Diều năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Đề thi cuối học kì 2 lớp 10 gồm có 4 phần:

• Phần 1: Trắc nghiệm khách quan
• Phần 2: Trắc nghiệm đúng sai
• Phần 3: Câu hỏi tự luận ngắn
• Phần 4: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT Cánh Diều Đề thi thử số 4

ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 10 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1. Tìm tập xác định của hàm số \(y = \frac{x + 2}{x - 1}\).

A. \(D\mathbb{= R}\backslash\left\{ 1 \right\}\).                   B. \(D\mathbb{= R}\backslash\left\{ 1;2 \right\}\).                 C. \(D\mathbb{= R}\).                 D. \(D\mathbb{= R}\backslash\left\{ 2 \right\}\).

Câu 2. Cho hàm số y = \(f(x) = \sqrt{x^{2}}\). Giá trị \(f(0)\) bằng

A. \(0\).                              B. \(2\).                         C. \(1\).                           D. không tồn tại.

Câu 3. Hàm số nào dưới đây là hàm số bậc hai?

A. \(y = - 2x^{4} + 3x^{2} + 5\).                                    B. \(y = \frac{- 1}{2x^{2}}\).

C. \(y = x^{2} + x - 3\).                                             D. \(y = 4\left( \frac{1}{x} \right)^{2} + \frac{1}{x} - 6\)

Câu 4. Đồ thị ở hình dưới đây là đồ thị của hàm số nào trong bốn hàm số sau?

A. \(y = 2x^{2} - 4x - 1\).                                       B. \(y = 2x^{2} - 4x - 3\).

C. \(y = 2x^{2} - 4x - 4\).                                       D. \(y = 2x^{2} - 4x - 2\).

Câu 5. Cho biểu thức \(f(x) = - x^{2} + 3x - 2\). Khẳng định nào sau đây đúng.

A. \(f(x) > 0,\forall x\mathbb{\in R}\).                                        B. \(f(x) < 0,\forall x \in ( - \infty;2)\).

C. \(f(x) < 0,\forall x \in (1; + \infty)\).                            D. \(f(x) > 0,\forall x \in (1;2)\).

Câu 6. Trong mặt phẳng tọa độ \(Oxy\), đường thẳng \(\Delta:2x - y + 2024 = 0\) có một véc tơ pháp tuyến là

A. \(\overrightarrow{n} = (1;2)\).                                                      B. \(\overrightarrow{n} = (4; - 2)\).

C. \(\overrightarrow{n} = (2;1)\).                                                      D. \(\overrightarrow{n} = ( - 2; - 1)\).

Câu 7. Trong mặt phẳng tọa độ \(Oxy\), đường thẳng \(d:\left\{ \begin{matrix} x = 1 - 2t \\ y = - 2 + 3t \\ \end{matrix} \right.\ \ ,\left( t\mathbb{\in R} \right)\) có phương trình tổng quát là

A. \(2x - 3y + 1 = 0.\)                                            B. \(2x + 3y + 1 = 0.\)

C. \(3x - 2y + 1 = 0.\)                                             D. \(3x + 2y + 1 = 0.\)

Câu 8. Cho 2 đường thẳng \(\Delta:x - y + 2 = 0\) và \(\Delta': - x + 1 = 0\). Góc giữa 2 đường thẳng \(\Delta\) và \(\Delta'\) bằng

A. \(90^{0}\).                          B. \(45^{0}\).                        C. \(135^{0}\).                      D. \(60^{0}\).

Câu 9. Trong mặt phẳng tọa độ \(Oxy\), cho đường tròn \((C):x^{2} + y^{2} + 2x - 4y - 4 = 0\). Xác định tâm và bán kính đường tròn

A. \(I(1; - 2),R = 3.\)                                          B. \(I(1; - 2),R = 9.\)

C. \(I( - 1;2),R = 9.\)                                         D. \(I( - 1;2),R = 3.\)

Câu 10. Cho \(2\) điểm \(A(1;\ 1)\), \(B(7;\ 5)\). Phương trình đường tròn đường kính \(AB\) là

A. \(x^{2} + y^{2} + 8x + 6y - 12 = 0\).                           B. \(x^{2} + y^{2} - 8x - 6y + 12 = 0\).

C. \(x^{2} + y^{2} + 8x + 6y + 12 = 0\).                            D. \(x^{2} + y^{2} - 8x - 6y - 12 = 0\).

Câu 11. Đường Elip \(\frac{x^{2}}{25} + \frac{y^{2}}{4} = 1\) có độ dài trục lớn bằng

A. 8.                       B. 10.                          C. 2.                                   D. 12.

Câu 12. Phương trình nào sau đây là phương trình chính tắc của đường hypebol?

A. \(\frac{x^{2}}{5} - \frac{y^{2}}{4} = - 1\).                                      B. \(\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1\).

C. \(\frac{x^{2}}{16} + \frac{y^{2}}{9} = - 1\).                                      D. \(\frac{x^{2}}{8} - \frac{y^{2}}{6} = 1\).

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI

Trong mỗi ý ở mỗi câu, hãy chọn đúng hoặc sai.

Câu 1. Cho hai đường thẳng \(\Delta_{1}:x - y - 3 = 0\)và \(\ \Delta_{2}:\left\{ \begin{matrix} x = 1 - t \\ y = 2 + 2t \\ \end{matrix} \right.\). Khi đó:

a) \(\Delta_{1}\), \(\Delta_{2}\) lần lượt có vectơ pháp tuyến là \({\overrightarrow{n}}_{1} = (1; - 1)\ ,\ \overrightarrow{n_{2}} = (2;1).\)

b) \(\Delta_{1},\Delta_{2}\) cắt nhau tại điểm có tọa độ \(\left( \frac{7}{2}; - \frac{2}{3} \right)\).

c) \(\cos\left( \Delta_{1},\Delta_{2} \right) = \frac{\sqrt{10}}{10}.\)

d) Khoảng cách giữa hai đường thẳng \(\Delta_{2}\) và \(\Delta_{3}: - 2x - y + 1 = 0\) bằng \(2\sqrt{5}.\)

Câu 2. Các mệnh đề sau đúng hay sai?

a) Tập xác định của hàm số \(y = \sqrt{5 - 4x - x^{2}}\) là \(D = \lbrack - 5;1\rbrack\).

b) Bình phương 2 vế phương trình \(\sqrt{2x^{2} + x - 6} = x + 2\) ta được phương trình\(x^{2} - 3x - 10 = 0\)

c) Cho tam thức \(f(x) = x^{2} - x - 2\) khi đó \(f(x) > 0\) với mọi \(x \in ( - 1;2)\).

d) Với \(m \geq \frac{1}{2}\) thì biểu thức \(f(x) = \left( m^{2} + 2 \right)x^{2} - 2(m + 1)x + 1\) luôn dương.

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.

Câu 1. Tính tổng các nghiệm của phương trình \(\sqrt{3x - 1}\ + \sqrt{3 - x}\ = \ \sqrt{x + \ 2}\ + \sqrt{x}\).

Câu 2. Cho hai điểm\(A(3; - 1),B(0;3)\). Tìm hoành độ điểm \(M\) thuộc \(Ox\) sao khoảng cách từ \(M\) đến đường thẳng\(AB\) bằng \(1\), biết hoành độ điểm \(M\)lớn hơn 2.

Câu 3. Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(d:2x - y - 5 = 0\) và hai điểm \(A(1;2),B(4;1)\). Tính bán kính đường tròn \((C)\) có tâm thuộc \(d\) và đi qua hai điểm \(A,B\).

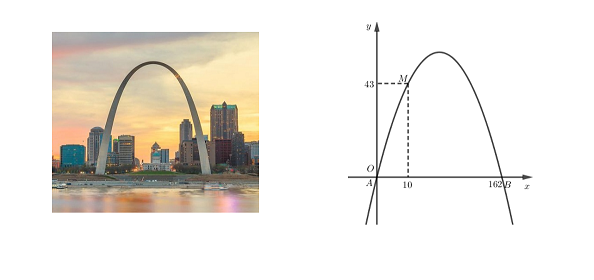
Câu 4. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng của một parabol. Biết khoảng cách giữa hai chân cổng là \(162\ m\). Trên thành cổng, tại vị trí có độ cao \(43\ m\) so với mặt đất, người ta thả một sợi dây chạm đất và vị trí chạm đất này cách chân cổng (điểm \(A\)) một khoảng \(10\ m\). Hãy tính gần đúng độ cao của cổng Arch (tính chính xác đến hàng đơn vị).

PHẦN IV. TỰ LUẬN

Câu 1. Vị trí của một chất điểm \(M\) tại thời điểm \(t\) (\(t\) trong khoảng thời gian từ 0 phút đến 180 phút) có toạ độ là \(\left( 3 + 5sint{^\circ};4 + 5\ \cos\ t{^\circ} \right)\). Tìm toạ độ của chất điểm \(M\) khi \(M\) ở cách xa gốc toạ độ nhất.

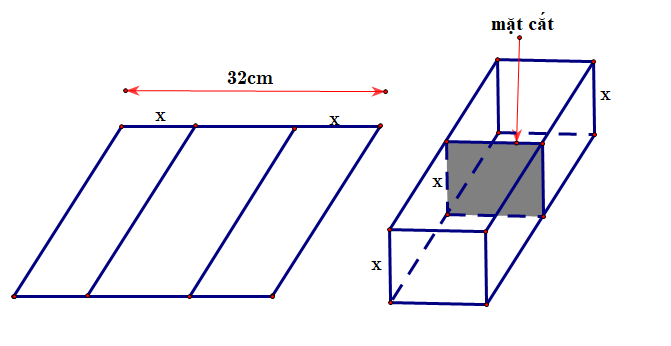
Câu 2. Một người muốn uốn tấm tôn phẳng hình chữ nhật có bề ngang 32 cm, thành một rãnh dẫn nước bằng cách chia tấm tôn đố thành ba phần rồi gấp hai bên lại theo một góc vuông như hình vẽ. Biết rằng diện tích mặt cắt ngang của rãnh nước phải lớn hơn hoặc bằng tổng \(120cm^{2}\). Hỏi độ cao tối thiểu và tối đa của rãnh dẫn nước là bao nhiêu cm?

Câu 3. Cho hàm số \(y = ax + b\). Tìm \(a\) và \(b\), biết rằng đồ thị hàm số đi qua điểm \(M( - 1;1)\) và cắt trục hoành tại điểm có hoành độ là \(5\).

……….………Hết………………..

Đáp án có trong file tải, mời bạn đọc tải tài liệu!