VnDoc.com

Đề thi học kì 2 Toán 10 Cánh Diều (Cấu trúc mới) năm 2025 Đề 5

Đề thi hk2 toán 10 - Có đáp án chi tiết

Bài trước

Tải về

Bài sau

Môn: Toán

Bộ sách: Cánh diều

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Đề thi học kì 2 môn Toán 10 Cánh Diều

Đề thi học kì 2 lớp 10 môn Toán Cánh Diều năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Đề thi cuối học kì 2 lớp 10 gồm có 4 phần:

Phần 1: Trắc nghiệm khách quan
Phần 2: Trắc nghiệm đúng sai
Phần 3: Câu hỏi tự luận ngắn
Phần 4: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT

Cánh Diều

Đề thi thử số 5

ĐỀ KIỂM TRA CUỐI HỌC KỲ II

MÔN: TOÁN - LỚP 10

NĂM HỌC: 2024 – 2025

Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Tập xác định của hàm số $y = \frac{5}{x^{2} - 1}$ $y = \frac{5}{x^{2} - 1}$ là

A. $\mathbb{R}\backslash\left\{ - 1 \right\}$ $\mathbb{R}\backslash\left\{ - 1 \right\}$. B. $\mathbb{R}\backslash\left\{ - 1;1 \right\}$ $\mathbb{R}\backslash\left\{ - 1;1 \right\}$. C. $\mathbb{R}\backslash\left\{ 1 \right\}$ $\mathbb{R}\backslash\left\{ 1 \right\}$. D. $\mathbb{R}$ $\mathbb{R}$.

Câu 2: Trong mặt phẳng $Oxy$, đỉnh của parabol $y = x^{2} - 2x - 1$ $y = x^{2} - 2x - 1$ có toạ độ là

A. $(2; - 1)$. B. $(1; - 2)$. C. $( - 1;2)$. D. $(1;2)$

Câu 3: Cho hàm số $y = f(x) = ax^{2} + bx + c$ $y = f(x) = ax^{2} + bx + c$ có đồ thị như hình vẽ. Đặt $\Delta = b^{2} - 4ac$ $\Delta = b^{2} - 4ac$, tìm dấu của $a$ và $\Delta$ $\Delta$.

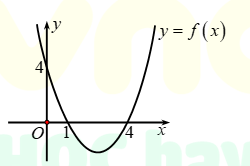
A. $a > 0$, $\Delta > 0$ $\Delta > 0$. B. $a < 0$, $\Delta > 0$ $\Delta > 0$.

C. $a > 0$, $\Delta = 0$ $\Delta = 0$. D. $a < 0$, $,\ \Delta = 0$ $,\ \Delta = 0$.

Câu 4: Phương trình $\sqrt{x^{2} + 4x - 1} = x - 3$ $\sqrt{x^{2} + 4x - 1} = x - 3$ có nghiệm là

A. $x = 1$ hoặc $x = 3$. C. $x = 1$.

B. Vô nghiệm. D. $x = 3$.

Câu 5: Đường thẳng $d$ có một vectơ chỉ phương là $\overrightarrow{u} = (3; - 4)$ $\overrightarrow{u} = (3; - 4)$. Đường thẳng $\Delta$ $\Delta$ vuông góc với $d$ có một vectơ pháp tuyến là:

A. $\overrightarrow{n_{1}} = (4;3).$ $\overrightarrow{n_{1}} = (4;3).$ B. $\overrightarrow{n_{2}} = ( - 4; - 3).$ $\overrightarrow{n_{2}} = ( - 4; - 3).$

C. $\overrightarrow{n_{3}} = (3;4).$ $\overrightarrow{n_{3}} = (3;4).$ D. $\overrightarrow{n_{4}} = (3; - 4).$ $\overrightarrow{n_{4}} = (3; - 4).$

Câu 6: Phương trình đường thẳng đi qua hai điểm $A(0;4),B( - 6;0)$ là:

A. $\frac{x}{6} + \frac{y}{4} = 1$ $\frac{x}{6} + \frac{y}{4} = 1$. B. $\frac{x}{4} + \frac{y}{- 6} = 1$ $\frac{x}{4} + \frac{y}{- 6} = 1$.

C. $\frac{- x}{4} + \frac{y}{- 6} = 1$ $\frac{- x}{4} + \frac{y}{- 6} = 1$. D. $\frac{- x}{6} + \frac{y}{4} = 1$ $\frac{- x}{6} + \frac{y}{4} = 1$.

Câu 7: Đường tròn có tâm $I(1;2)$, bán kính $R = 3$ có phương trình là:

A. $x^{2} + y^{2} + 2x + 4y - 4 = 0$ $x^{2} + y^{2} + 2x + 4y - 4 = 0$ B. $x^{2} + y^{2} + 2x - 4y - 4 = 0$ $x^{2} + y^{2} + 2x - 4y - 4 = 0$

C. $x^{2} + y^{2} - 2x + 4y - 4 = 0$ $x^{2} + y^{2} - 2x + 4y - 4 = 0$ D. $x^{2} + y^{2} - 2x - 4y - 4 = 0$ $x^{2} + y^{2} - 2x - 4y - 4 = 0$

Câu 8: Elip $(E):\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ $(E):\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ có tiêu cự bằng:

A. $\sqrt{5}$ $\sqrt{5}$ B. $5$ C. $10$ D. $2\sqrt{5}$ $2\sqrt{5}$

Câu 9: Một thùng trong đó có $12$ hộp đựng bút màu đỏ, $18$ hộp đựng bút màu xanh. Số cách khác nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là?

A. $13.$ B. $12.$ C. $18.$ D. $216.$

Câu 10: Một tổ có $10$ học sinh. Hỏi có bao nhiêu cách chọn ra $2$ học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó.

A. $A_{10}^{2}$ $A_{10}^{2}$. B. $C_{10}^{2}$ $C_{10}^{2}$. C. $A_{10}^{8}$ $A_{10}^{8}$. D. $10^{2}$ $10^{2}$.

Câu 11: Số hạng thứ $13$ trong khai triển $(2 - x)^{15}$ $(2 - x)^{15}$ bằng?

A. $3640x^{13}$ $3640x^{13}$. B. $3640x^{12}$ $3640x^{12}$. C. $- 420x^{12}$ $- 420x^{12}$. D. $3640$.

Câu 12: Từ một hộp chứa $11$ quả cầu màu đỏ và $4$ quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được $3$ quả cầu màu xanh

A. $\frac{33}{91}$ $\frac{33}{91}$ B. $\frac{24}{455}$ $\frac{24}{455}$ C. $\frac{4}{165}$ $\frac{4}{165}$ D. $\frac{4}{455}$ $\frac{4}{455}$

PHẦN II. CÂU HỎI TRẮC NGHIỆM ĐÚNG SAI

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Chuyển động của vật thể $M$ được thể hiện trên mặt phẳng toạ độ $Oxy$. Vật thể $M$ khởi hành từ điểm $A(5;3)$ và chuyển động thẳng đều với vectơ vận tốc là $\overrightarrow{v}(1;2)$ $\overrightarrow{v}(1;2)$. Khi đó:

a) Vectơ chỉ phương của đường thẳng biểu diễn chuyển động của vật thể là $\overrightarrow{v}(1;2)$ $\overrightarrow{v}(1;2)$

b) Vật thể $M$ chuyển động trên đường thẳng $2x - 3y - 1 = 0$

c) Toạ độ của vật thể $M$ tại thời điểm $t(t > 0)$ tính từ khi khởi hành là $\left\{ \begin{matrix} x = 5 + t \\ y = 3 + 2t \\ \end{matrix} \right.$ $\left\{ \begin{matrix} x = 5 + t \\ y = 3 + 2t \\ \end{matrix} \right.$

d) Khi $t = 5$ thì vật thể $M$ chuyển động được quãng đường dài bằng $5\sqrt{5}$ $5\sqrt{5}$

Câu 2: Một trường cấp 3 của tỉnh Đồng Tháp có 8 giáo viên Toán gồm có 3 nữ và 5 nam, giáo viên Vật lý thì có 4 giáo viên nam, chọn ra một đoàn thanh tra công tác ôn thi THPTQG, khi đó

a) Chọn 1 giáo viên nữ có $C_{3}^{1}$ $C_{3}^{1}$ cách

b) Chọn 2 giáo viên nam môn Vật lý có $C_{4}^{2}$ $C_{4}^{2}$ cách.

c) Chọn 1 giáo viên nam môn Toán và 1 nam môn Vật lý có $C_{5}^{1} + C_{4}^{1}$ $C_{5}^{1} + C_{4}^{1}$ cách.

d) Có 80 cách chọn ra một đoàn thanh tra công tác ôn thi THPTQG gồm 3 người có đủ 2 môn Toán và Vật lý và phải có giáo viên nam và giáo viên nữ trong đoàn

PHẦN III. CÂU HỎI TỰ LUẬN NGẮN

Câu 1: Từ bộ bài tây gồm 52 quân bài, người ta rút ra ngẫu nhiên 2 quân bài. Xác suất để rút được 2 quân bài khác màu có dạng $\frac{a}{b}$ $\frac{a}{b}$ với a,b là số nguyên dương và phân số $\frac{a}{b}$ $\frac{a}{b}$ là phân số tối giản. Tính giá trị biểu thức $P = b - a$

Câu 2: Tính tổng các nghiệm của phương trình sau: $\sqrt{3x^{2} - 9x + 1} = |x - 4|$ $\sqrt{3x^{2} - 9x + 1} = |x - 4|$

Câu 3: Một đường tròn có tâm $I(3\ ;\ 4)$ $I(3\ ;\ 4)$ tiếp xúc với đường thẳng $\Delta:\ 3x + 4y - 10 = 0$ $\Delta:\ 3x + 4y - 10 = 0$. Hỏi bán kính đường tròn bằng bao nhiêu?

Câu 4: Đội thanh niên xung kích có của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp $A,4$ học sinh lớp $B$ và 3 học sinh lớp $C$ cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong ba lớp trên. Hỏi có bao nhiêu cách chọn như vậy?

PHẦN IV. CÂU HỎI TỰ LUẬN

Câu 1: Ban chấp hành Đoàn thanh niên của nhà trường cần lập $4$ đội cờ đỏ để chấm thi đua, mỗi đội $3$ người từ $12$ học sinh gồm $5$ học sinh lớp $12$, $4$ học sinh lớp $11$, $3$ học sinh lớp $10$. Tính xác suất để đội nào cũng có học sinh lớp $12$ và học sinh lớp $11$.

Câu 2: Cho hai đường thẳng song song $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$. Trên $d_{1}$ $d_{1}$ lấy 17 điểm phân biệt, trên $d_{2}$ $d_{2}$ lấy 20 điểm phân biệt. Tính số tam giác có các đỉnh là 3 điểm trong số 37 điểm đã chọn trên $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$.

Câu 3: Thiết kế khu vườn Hạnh Phúc hình vuông cạnh $10m$ như hình vẽ.

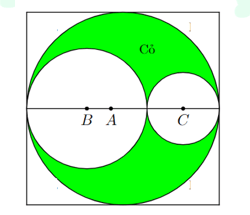
Phần được tô đậm dùng để trồng cỏ, phần còn lại lát gạch. Biết mỗi mét vuông trồng cỏ chi phí $100$ nghìn đồng, mỗi mét vuông lát gạch chi phí $300$ nghìn đồng. Khi diện tích phần lát gạch là nhỏ nhất thì tổng chi phí thi công vườn hoa Hạnh Phúc bằng (làm tròn đến hàng nghìn)?

------ HẾT ------

Đáp án có trong file tải, mời bạn đọc tải tài liệu!

Tải về

Chọn file muốn tải về: