Đề thi thử THPT Quốc gia 2024 môn Toán trường THPT Ngô Thì Nhậm, Ninh Bình
Thi THPT Quốc gia 2024
SỞ GD&ĐT NINH BÌNH
TRƯỜNG THPT NGÔ THÌ NHẬM
(Đề thi có 6 trang)
ĐỀ THI THỬ TNTHPT LẦN 1, NĂM 2024
Môn: Toán - Khối 12
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 111
Câu 1. Có bao nhiêu cách xếp 4 bạn vào một dãy gồm 4 chiếc ghế sao cho mỗi chiếc ghế có đúng
một học sinh ngồi?
A. 4. B. 12. C. 16. D. 24.
Câu 2. Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch
biến trên khoảng nào dưới đây?
x
y
0
−∞
−1
1
+∞
− −
0
+
A. (−1; +∞). B. (1; +∞). C. (−∞; 1). D. (−∞; −1).
Câu 3. Số phức liên hợp của số phức z = −3 + 2i là
A. z = −3 − 2i. B. z = 3 − 2i. C. z = 2 − 3i. D. z = 3 + 2i.
Câu 4. Hàm số y = x
π
+ (x
2
− 1)
e
có tập xác định D là
A. D = (−1; 1). B. D = R. C. D = (1; +∞). D. D = R \ {−1; 1}.
Câu 5. Điểm nào dưới đây thuộc đồ thị hàm số y = −x
4
+ 2x
2
− 3?
A. M(1; 2). B. Q(1; 1). C. P(1; −1). D. N(1; −2).
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với BC = a và đường cao SA = 3a.
Thể tích khối chóp S.ABCD bằng
A. a
3
√
3. B. 3a
3
. C. a
3
. D.
a
3
3
.
Câu 7. Tính đạo hàm của hàm số f(x) = e
πx+1
.
A. f
0
(x) = e
πx+1
ln π. B. f
0
(x) = πe
πx+1
. C. f
0
(x) = πe
πx
. D. f
0
(x) = e
πx
ln(π).
Câu 8. Số đường tiệm cận của đồ thị hàm số y =
4x + 5
x − 1
là
A. 1. B. 3. C. 0. D. 2.
Câu 9. Họ các nguyên hàm của hàm số f(x) = 2x + cos 2x là
A. x
2
+ sin 2x + C. B. x
2
+
1
2
sin 2x + C. C. x
2
−
1
2
sin 2x + C. D. x
2
− sin 2x + C.
Câu 10.
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M
như hình vẽ?
A. (1 + i)(2 −i). B.
i
2 + 3i
.
C. (1 + i)(2 − 3i). D.
3 − 2i
i
.
x
y
O
−2
M
−3
Câu 11. Trong không gian Oxyz, tìm tọa độ tâm I và bán kính R của mặt cầu có phương trình
(x − 1)
2
+ (y + 2)
2
+ (z − 4)
2
= 20.
A. I(1; −2; 4), R = 2
√
5. B. I(1; −2; 4), R = 20.
C. I(−1; 2; −4), R = 5
√
2. D. I(−1; 2; −4), R = 2
√
5.
Trang 1/6 − Mã đề 111
Câu 12. Biết
1
Z
0
f(x) dx = −3,
1
Z
0
g(x) dx = 4, khi đó
1
Z
0
[f(x) − g(x)] dx bằng
A. 7. B. −7. C. 1. D. −12.
Câu 13. Biết
3
Z
2
f(x) dx = 4 và
3
Z
2
g(x) dx = 1. Khi đó
3
Z
2
[f(x) − g(x)] dx bằng
A. 3. B. −3. C. 5. D. 4.
Câu 14. Trong không gian Oxyz, mặt phẳng nào dưới đây có véc-tơ pháp tuyến là
−→
n =
(1; −2; 3)?
A. x − 2z + 3 = 0. B. 2x + 4y −6z −1 = 0.
C. x − 2y + 3 = 0. D. −x + 2y − 3z + 2 = 0.
Câu 15. Cho số phức z = −2i + 3. Tìm số phức w = iz − 3z?
A. −7 − 3i. B. 7 − 3i. C. −7 + 3i. D. 7 + 3i.
Câu 16. Trong không gian Oxyz, đường thẳng d :
x = 1 + 2t
y = 3 − t
z = 1 − t
đi qua điểm nào sau đây?
A. N(1; 3; −1). B. P (1; 2; −3). C. Q(3; 5; 3). D. M(−3; 5; 3).
Câu 17.
Đồ thị như hình bên là của hàm số nào?
A. y = −x
3
+ 3x
2
+ 1. B. y = x
3
− 3x − 1.
C. y = x
3
− 3x + 1. D. y = −x
3
− 3x
2
− 1.
x
y
O
−1
3
1
−1
1
Câu 18. Cho hàm số y = f(x) có tập xác định (−∞; 4] và có bảng biến thiên như hình vẽ.
x
y
0
y
−∞
1 2 3
+∞
+
0
− +
0
−
−∞−∞
11
00
22
−1−1
Số điểm cực trị của hàm số đã cho là
A. 4. B. 3. C. 2. D. 5.
Câu 19. Tính giá trị biểu thức P =
ln a
2
b
3
ln a
3
b
2
. Biết ln a = 2023 và ln b = 2024.
A.
10118
10117
. B.
108
2019
. C.
10108
2021
. D.
2018
2019
.
Câu 20. Trên mặt phẳng tọa độ Oxy, biết M(5; −3) là điểm biểu diễn số phức liên hợp của số
phức z. Phần thực của z bằng
A. 2. B. 5. C. −3. D. 3.
Câu 21. Tập nghiệm của phương trình log
3
(x − 3) = log
3
(2x − 1) là
A. ∅. B. {2}. C. {−2}. D. {1}.
Trang 2/6 − Mã đề 111
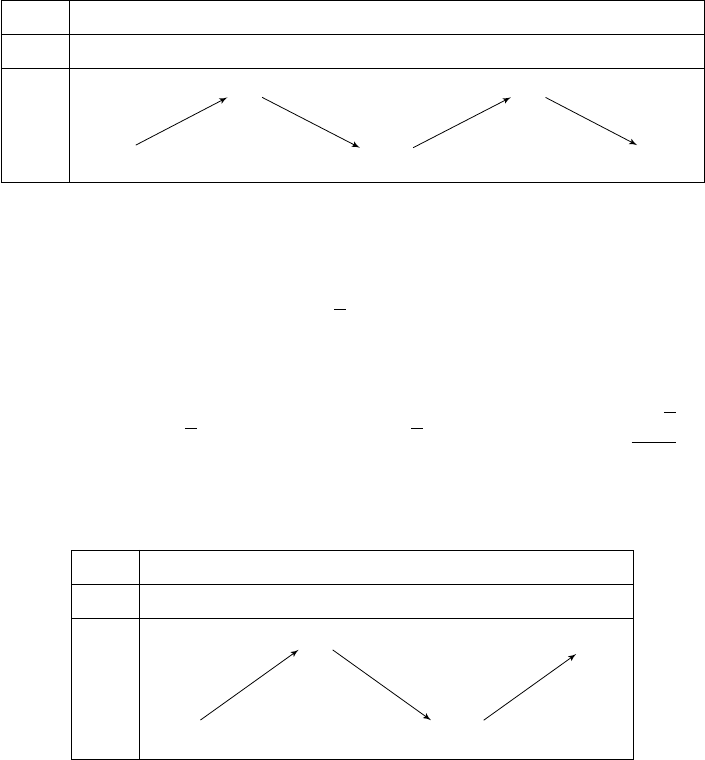
Câu 22. Cho hàm số y = f(x) = ax
4
+ bx
2
+ c (a, b, c ∈ R) có bảng biến thiên như hình vẽ
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Điểm cực tiểu của hàm số đã cho là
A. 2. B. 3. C. −1. D. 0.
Câu 23. Tập nghiệm của bất phương trình
1
3
x
≥ 9 là
A. (−∞; 2). B. [−2; +∞). C. (−∞; −2). D. (−∞; −2].
Câu 24. Cho mặt cầu có diện tích bằng 16πa
2
. Khi đó, bán kính mặt cầu bằng
A. 2a. B. 2
√
2a. C.
√
2a. D.
a
√
2
2
.
Câu 25. Cho hàm y = f(x) xác định, liên tục trên đoạn [−4; 4] và có bảng biến thiên trên [−4; 4]
như sau
x
y
0
y
−4 −2
0 4
+
0
−
0
+
−10−10
00
−4−4
1010
Giá trị lớn nhất của hàm số f(x) trên đoạn [−4; 4] là
A. 0. B. 4. C. 10. D. −2.
Câu 26. Cho a và b là hai số thực dương thỏa mãn a
4
b = 16. Giá trị của 4 log
2
a + log
2
b bằng
A. 8. B. 4. C. 16. D. 2.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho véc-tơ
−→
u = (2; 0; −1). Tìm véc-tơ
−→
v biết
−→
v
cùng phương với
−→
u và
−→
u ·
−→
v = 20.
A. (8; 0; 4). B. (8; 0; −4). C. (−8; 0; 4). D. (4; 0; −2).
Câu 28. Cho tích phân
2
Z
1
[4f(x) − 2x] dx = 1. Khi đó
2
Z
1
f(x) dx bằng
A. 1. B. −3. C. −1. D. 3.
Câu 29. Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy bằng 3 và chiều cao bằng
4 là
A. 36π. B. 24π. C. 12π. D. 42π.
Câu 30. Tính thể tích khối hộp chữ nhật có độ dài ba cạnh lần lượt là 2; 3 và 4.
A. 4. B. 8. C. 24. D. 12.
Câu 31. Tìm họ nguyên hàm của hàm số f(x) = 1 − 2 sin x.
A.
Z
(1 − 2 sin x) dx = x + 2 cos x + C. B.
Z
(1 − 2 sin x) dx = 1 + 2 cos x + C.
C.
Z
(1 − 2 sin x) dx = x − 2 cos x + C. D.
Z
(1 − 2 sin x) dx = −2 cos x + C.
Trang 3/6 − Mã đề 111
Đề thi thử tốt nghiệp THPT Quốc gia 2024 môn Toán trường THPT Ngô Thì Nhậm, Ninh Bình
Đề thi thử THPT Quốc gia 2024 môn Toán trường THPT Ngô Thì Nhậm, Ninh Bình được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 4 mã đề thi. Mỗi đề thi có 50 câu hỏi trắc nghiệm. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án và lời giải chi tiết kèm theo. Mời các bạn cùng theo dõi và tham khảo thêm đề thi các môn tại mục Thi THPT Quốc gia nhé.
