Đề thi thử THPT Quốc gia môn Toán lần 3 năm 2015 trường THPT Hàn Thuyên, Bắc Ninh
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia môn Toán lần 3 năm 2015 trường THPT Hàn Thuyên, Bắc Ninh là đề thi thử đại học môn Toán có đáp án mà VnDoc xin được gửi đến các bạn tham khảo, ôn tập, làm thử đề thi THPT Quốc gia môn Toán các trường trên cả nước, chuẩn bị tốt nhất cho kì thi quan trọng sắp diễn ra.
Đề thi thử THPT Quốc gia môn Vật lý lần 3 năm 2015 trường THPT Hàn Thuyên, Bắc Ninh
Đề thi thử THPT Quốc gia môn Sinh học lần 3 năm 2015 trường THPT Hàn Thuyên, Bắc Ninh
Đề thi thử THPT Quốc gia môn Hóa học lần 3 năm 2015 trường THPT Hàn Thuyên, Bắc Ninh
|
SỞ GD & ĐT BẮC NINH
|
ĐỀ THI THỬ KỲ THI THPT QUỐC GIA LẦN 3 NĂM HỌC 2014 – 2015 MÔN: TOÁN Thời gian: 180 phút (không kể thời gian phát đề) |
Câu 1 (2,0 điểm).
| Cho hàm số y = | 2x + 3 | có đồ thị (C) |
| x + 2 |
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số.
b) Tìm tất cả các giá trị của tham số m để đường thẳng d: y = x + 2m cắt đồ thị (C) tại 2 điểm phân biệt.
Câu 2 (1,0 điểm).
a) Giải phương trình: √2cos2x + sinx - cosx = 0.
b) Giải bất phương trình: 32x+1 - 4.(1/3)-x + 1 < 0.
Câu 3 (0,5 điểm). Cho số phức z thỏa mãn: (1 + i)z = 14 - 2i. Tìm mô đun của số phức z.
Câu 4 (1,0 điểm). Giải bất phương trình: ![]()
Câu 5 (1,0 điểm). Tính tích phân ![]()
Câu 6 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BC = 2AB. Mặt bên SAB là một tam giác vuông cân tại A và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC và côsin của góc giữa hai đường thẳng
AB và SC, biết SA = a.
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(5; 3), B(-4; 6). Gọi I là tâm đường tròn nội tiếp tam giác ABC. Đường thẳng qua I và song song với AB cắt BC tại F(-11/4; 9/4). Tìm tọa độ đỉnh C của tam giác ABC.
Câu 8 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3; -1; -3), B(1; 0; -1) và mặt phẳng (P): 2x + y - 2z - 2 = 0. Gọi C là hình chiếu vuông góc của điểm A trên mặt phẳng (P). Tìm tọa độ điểm C và viết phương trình mặt phẳng (ABC).
Câu 9 (0,5 điểm). Một lớp khối 12 có 26 học sinh giỏi, trong đó có 10 học sinh giỏi là học sinh nam, 16 học sinh giỏi là học sinh nữ và lớp trưởng là học sinh giỏi nữ, bí thư chi đoàn là học sinh giỏi nam. Nhà trường cử 4 học sinh giỏi của lớp đi dự hội nghị tổng kết năm học. Tính xác suất sao cho trong số 4 học sinh được chọn chỉ có 1 cán bộ lớp (lớp trưởng hoặc bí thư), có cả học sinh giỏi nam và học sinh giỏi nữ.
Câu 10 (1,0 điểm). Tìm giá trị nhỏ nhất của biểu thức:
![]()
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1 (2,0 điểm)
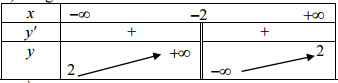
a. Tập xác định: D = R \ {-2}
- Sự biến thiên:
| lim y | = 2 | lim y | = 2 | → y = 2 là tiệm cận ngang của đồ thị. |
| x→-∞ | x→+∞ |
| lim y | = +∞ | lim y | = -∞ | → x = -2 là tiệm cận ngang của đồ thị. |
| x→-2- | x→-2+ |
+ y' = 1/(x + 2)2 > 0 ∀x ≠ -2 → hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞).
Không có cực trị.
+ Bảng biến thiên
- Đồ thị
b) Phương trình hoành độ giao điểm: (2x + 3)/(x + 2) = x + 2m
↔ 2x + 3 = (x + 2m)(x + 2) (x ≠ -2)
↔ x2 + 2mx + 4m - 3 = 0 (1)
Đường thẳng (d) cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt x ≠ -2.
| ↔ { | m2 - 4m + 3 > 0 | ↔ [ | m > 3 |
| (-2)2 + 2m(-2) + 4m - 3 ≠ 0 | m < 1 |
Vậy với m ∈ (-∞; 1) υ (3; +∞) thì (d) cắt đồ thị (C) tại 2 điểm phân biệt.
Câu 2 (1,0 điểm).
a) Giải phương trình: √2cos2x + sinx - cosx = 0
Phương trình ↔ cos2x = cos(x + π/4)
| ↔ [ | 2x = x + π/4 + k2π |
| 2x = -x - π/4 + k2π |
Thu gọn ta được: x = π/4 + k2π; x = -π/12 + k2π/3.


