Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bắc Giang

Đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2016 tỉnh Bắc Giang có đáp án đi kèm, gồm 10 câu hỏi kiểm tra kiến thức cần thiết để các bạn học sinh luyện thi THPT Quốc gia, ôn thi Đại học hiệu quả. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Thanh Chương 1, Nghệ An

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC GIANG (đề thi gồm 01 trang)

KỲ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 MÔN: TOÁN Ngày thi: 08/4/2016 Thời gian làm bài 180 phút, không kể phát đề

Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị hàm số

Câu 2 (1,0 điểm). Gọi M là giao điểm của đồ thị hàm số y = -x³ + 3x² - 2 (C) và đường thẳng y = x + 3.

Viết phương trình tiếp tuyến với đồ thị (C) tại điểm M.

Câu 3 (1,0 điểm).

a) Giải phương trình cosx + sinx = 1 + sin2x + cos2x.

b) Giải phương trình log₂(x² - 1) = log_1/2(x - 1).

Câu 4 (1,0 điểm). Tính tích phân

Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z - 3 = 0, đường thẳng và điểm A(2;5;8). Viết phương trình mặt phẳng (Q) qua A và vuông góc với đường thẳng d. Tìm tọa độ điểm B thuộc d sao cho khoảng cách từ B đến mặt phẳng (P) bằng 8/3.

Câu 6 (1,0 điểm).

a) Cho khai triển (1 + 2x)ⁿ = a₀ + a₁x + a₂x² + ... + a_nxⁿ. Tìm số nguyên dương n biết a₀ + 8a₁ = 2a₂ + 1.

b) Gọi A là tập các số tự nhiên có 6 chữ số đôi một khác nhau lập được từ các chữ số 0, 2, 3, 5, 6, 8. Lấy ngẫu nhiên một số thuộc tập A. Tính xác suất để số lấy được có chữ số 0 và chữ số 5 không đứng cạnh nhau.

Câu 7 (1,0 điểm). Cho lăng trụ ABC.A'B'C', có đáy là một tam giác đều cạnh bằng 2a. Hình chiếu vuông góc của B lên mặt phẳng (A'B'C') trùng với trung điểm H của cạnh B'C', K là điểm trên cạnh AC sao cho CK=2AK và BA' = 2a√3. Tính thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa hai đường thẳng CC' và BK theo a.

Câu 8 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có phương trình AD: x - 2y + 3 = 0. Trên đường thẳng qua B và vuông góc với đường chéo AC lấy điểm E sao cho BE = AC (D và E nằm về hai phía so với đường thẳng AC). Xác định tọa độ các đỉnh của hình chữ nhật ABCD, biết điểm E(2;-5), đường thẳng AB đi qua điểm F(4; 4)  và điểm B có hoành độ dương.

Câu 9 (1,0 điểm). Giải hệ phương trình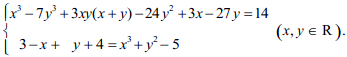

Câu 10 (1,0 điểm). Cho ba số thực dương x, y, z thỏa mãn xy + yz + zx + xyz = 4.

Chứng minh rằng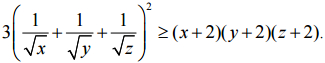

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán

Câu 1:

TXĐ: D = R \ {1}

Sự biến thiên:

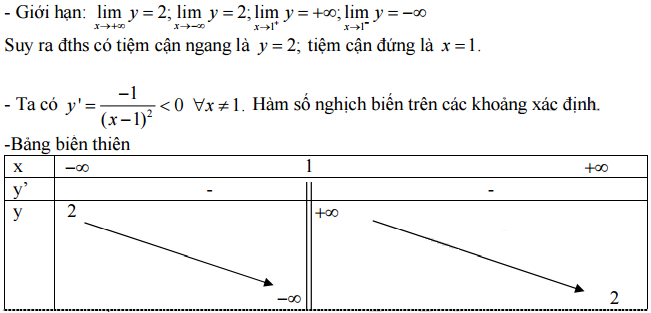
(Còn tiếp)