Giải bài tập Toán 10 SBT bài 3 chương 4
Toán 10 - Dấu của nhị thức bậc nhất
VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT bài 3 chương 4, tài liệu kèm theo đáp án sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán lớp 10 một cách chính xác nhất. Mời các bạn học sinh và thầy cô cùng tham khảo.
Giải bài tập Toán 10 SBT bài 2 chương 3
Giải bài tập Toán 10 SBT bài 3 chương 3
Giải bài tập Toán 10 SBT bài 3
Bài 27 trang 114 Sách bài tập Toán 10
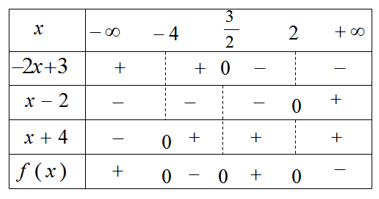
Xét dấu biểu thức sau:
f(x)=(−2x+3)(x−2)(x+4)
Gợi ý làm bài
Bài 28 trang 114 Sách bài tập (SBT) Toán Đại số 10
Xét dấu biểu thức sau:
![]()
Gợi ý làm bài
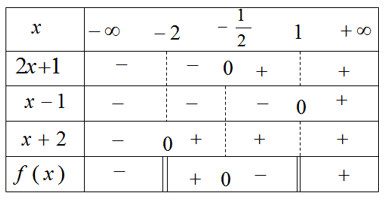
Bài 29 trang 114 Sách bài tập (SBT) Toán Đại số 10
Xét dấu biểu thức sau:
![]()
Gợi ý làm bài
![]()
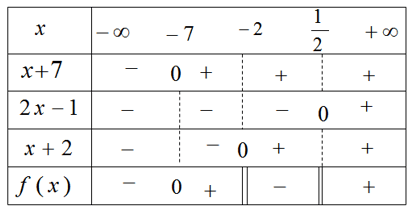
Bài 30 trang 114 Sách bài tập (SBT) Toán Đại số 10
Xét dấu biểu thức sau:
f(x)=(4x−1)(x+2)(3x−5)(−2x+7)
Gợi ý làm bài

Bài 31 trang 114 Sách bài tập (SBT) Toán Đại số 10
Giải bất phương trình sau
![]()
Gợi ý làm bài

Bài 32 trang 114 Sách bài tập (SBT) Toán Đại số 10
Giải bất phương trình sau:
![]()
Gợi ý làm bài
![]()
![]()
Bảng xét dấu vế trái của (1)
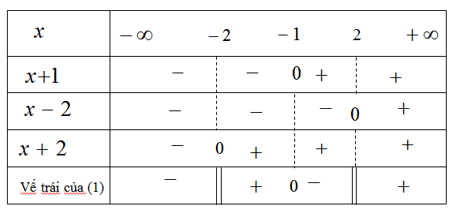
Đáp số: −2<x≤−1,x>2
Bài 33 trang 114 Sách bài tập (SBT) Toán Đại số 10
Giải bất phương trình sau:
![]()
Gợi ý làm bài
![]()
![]()
![]()
![]()
Bảng xét dấu vế trái của (1)
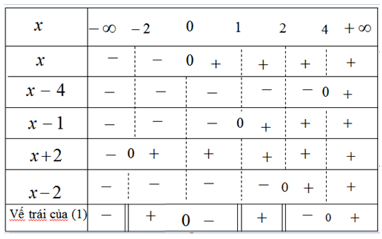
Đáp số: ![]()
Bài 34 trang 114 Sách bài tập (SBT) Toán 10
Giải bất phương trình sau:
|x−3|>−1|
Gợi ý làm bài
Vì |x−3|≥0,∀x nên |x−3|>−1,∀x
Tập nghiệm của bất phương trình là (−∞;+∞)
Bài 35 trang 114 Sách bài tập (SBT) Toán Đại số 10
Giải bất phương trình sau:
![]()
Gợi ý làm bài
![]()
![]()
Đáp số: ![]()
Bài 36 trang 114 Sách bài tập (SBT) Toán Đại số 10
Giải bất phương trình sau:
|x+2|+|−2x+1|≤x+1
Gợi ý làm bài
Bỏ dấu giá trị tuyệt đối ở vế trái của bất phương trình ta có:
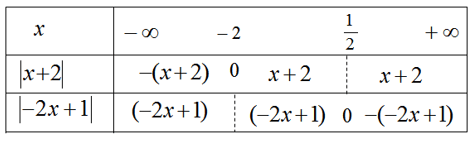
Bất phương trình đã cho tương đương với
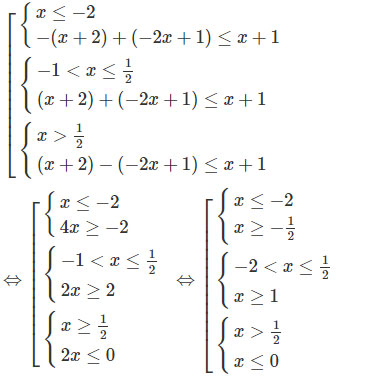
(Vô nghiệm)
Vậy bất phương trình đã cho vô nghiệm.
-----------------------------
Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.