Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập Toán 10 SBT ôn tập chương 3

Phương trình. Hệ phương trình

Toán 10 - Phương trình. Hệ phương trình

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 10 SBT ôn tập chương 3, tài liệu kèm theo lời giải chi tiết sẽ giúp các bạn học sinh rèn luyện giải bài tập Toán lớp 10 một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.

Giải bài tập Toán 10 SBT ôn tập chương 2

Giải bài tập Toán 10 SBT bài 1 chương 3

Giải bài tập Toán 10 SBT bài 2 chương 3

Giải bài tập Toán 10 SBT bài 3 chương 3

Giải bài tập Toán 10 SBT

Bài 19 trang 77 Sách bài tập (SBT) Toán Đại số 10

Hãy viết điều kiện của mỗi phương trình

a) $\sqrt { - 3x + 2} = {2 \over {x + 1}}$ $\sqrt { - 3x + 2} = {2 \over {x + 1}}$

b) $\sqrt {x - 2} + x = 3{x^2} + 1 - \sqrt { - x - 4}$ $\sqrt {x - 2} + x = 3{x^2} + 1 - \sqrt { - x - 4}$

c) ${{3x + 5} \over {\sqrt {3{x^2} + 6x + 11} }} = \sqrt {2x + 1}$ ${{3x + 5} \over {\sqrt {3{x^2} + 6x + 11} }} = \sqrt {2x + 1}$

d) ${{\sqrt { - 3x + 2} } \over {{x^2} - 9}} = x + 2$ ${{\sqrt { - 3x + 2} } \over {{x^2} - 9}} = x + 2$

Gợi ý làm bài

Điều kiện của mỗi phương trình:

a) $x \le {2 \over 3}$ $x \le {2 \over 3}$ và $x \ne - 1$ $x \ne - 1$

b) ) x≥2 và x≤−4. Không có số thực x nào thỏa mãn điều kiện của phương trình.

c) $3{x^2} + 6x + 11 > 0$ $3{x^2} + 6x + 11 > 0$ và $x \ge - {1 \over 2}$ $x \ge - {1 \over 2}$ . Vì ta có $3{x^2} + 6x + 11 = 3{(x + 1)^2} + 8 > 0$ $3{x^2} + 6x + 11 = 3{(x + 1)^2} + 8 > 0$ với mọi x, nên điều kiện của phương trình là $x \ge - {1 \over 2}$ $x \ge - {1 \over 2}$

d) x≥−4 và x≠3,x≠−3

Bài 20 trang 77 Sách bài tập (SBT) Toán Đại số 10

Xác định m để mỗi cặp phương trình sau tương đương

a) $3x - 1 = 0$ và ${{3mx + 1} \over {x - 2}} + 2m - 1 = 0$ ${{3mx + 1} \over {x - 2}} + 2m - 1 = 0$

b) ${x^2} + 3x - 4 = 0$ ${x^2} + 3x - 4 = 0$ và $m{x^2} - 4x - m + 4 = 0$ $m{x^2} - 4x - m + 4 = 0$

Gợi ý làm bài

Hai phương trình tương đương khi chúng có cùng tập nghiệm.

a) $3x - 1 = 0 \Leftrightarrow x = {1 \over 3}$ $3x - 1 = 0 \Leftrightarrow x = {1 \over 3}$

Suy ra $x = {1 \over 3}$ $x = {1 \over 3}$ là nghiệm của phương trình ${{3mx + 1} \over {x - 2}} + 2m - 1 = 0$ ${{3mx + 1} \over {x - 2}} + 2m - 1 = 0$

$\Rightarrow {{3m.{1 \over 3} + 1} \over {{1 \over 3} - 2}} + 2m - 1 = 0 \Leftrightarrow m = {8 \over 7}$ $\Rightarrow {{3m.{1 \over 3} + 1} \over {{1 \over 3} - 2}} + 2m - 1 = 0 \Leftrightarrow m = {8 \over 7}$

$x_{}^2 + 3x - 4 = 0 \Leftrightarrow \left\{ \matrix{x = 1 \hfill \cr x = - 4 \hfill \cr} \right.$ $x_{}^2 + 3x - 4 = 0 \Leftrightarrow \left\{ \matrix{x = 1 \hfill \cr x = - 4 \hfill \cr} \right.$

Suy ra x = 1 và x = -4 là nghiệm của phương trình $mx_{}^2 - 4x - m + 4 = 0$ $mx_{}^2 - 4x - m + 4 = 0$

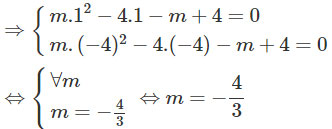
Giải bài tập Toán 10 SBT ôn tập chương 3

Bài 21 trang 77 Sách bài tập (SBT) Toán Đại số 10

Giải và biện luận các phương trình sau theo tham số m

a) $2m(x - 2) + 4 = (3 - {m^2})x$ $2m(x - 2) + 4 = (3 - {m^2})x$

b) ${{(m + 3)x} \over {2x - 1}} = 3m + 2$ ${{(m + 3)x} \over {2x - 1}} = 3m + 2$

c) ${{8mx} \over {x + 3}} = (4m + 1)x + 1$ ${{8mx} \over {x + 3}} = (4m + 1)x + 1$

d) ${{(2 - m)x} \over {x - 2}} = (m - 1)x - 1$ ${{(2 - m)x} \over {x - 2}} = (m - 1)x - 1$

Gợi ý làm bài

a) Phương trình đã cho tương đương với phương trình

$(m - 1)(m + 3)x = 4(m - 1)$

Với m≠1 và m≠−3 phương trình có nghiệm $x = {4 \over {m + 3}};$ $x = {4 \over {m + 3}};$

Với m = 1 mọi số thực x đều là nghiệm của phương trình;

Với m = -3 phương trình vô nghiệm.

b) Điều kiện của phương trình là $m \ne {1 \over 2}$ $m \ne {1 \over 2}$. Khi đó ta có

${{(m + 3)x} \over {2x - 1}} = 3m + 2 \Leftrightarrow (m + 2)x = (3m + 2)(2x - 1)$ ${{(m + 3)x} \over {2x - 1}} = 3m + 2 \Leftrightarrow (m + 2)x = (3m + 2)(2x - 1)$

$\Leftrightarrow (5m + 1)x = 3m + 2$ $\Leftrightarrow (5m + 1)x = 3m + 2$

Nếu $m \ne - {1 \over 5}$ $m \ne - {1 \over 5}$ thì phương trình có nghiệm $x = {{3m + 2} \over {5m + 1}}$ $x = {{3m + 2} \over {5m + 1}}$

Giá trị này là nghiệm của phương trình đã cho khi

${{3m + 2} \over {5m + 1}} \ne {1 \over 2} \Leftrightarrow 6m + 4 \ne 5m + 1 \Leftrightarrow m \ne - 3$ ${{3m + 2} \over {5m + 1}} \ne {1 \over 2} \Leftrightarrow 6m + 4 \ne 5m + 1 \Leftrightarrow m \ne - 3$

Nếu $m = - {1 \over 5}$ $m = - {1 \over 5}$ phương trình cuối vô nghiệm.

Kết luận.

Với $m = - {1 \over 5}$ $m = - {1 \over 5}$ và $m = - 3$ phương trình đã cho vô nghiệm.

Với $m \ne - {1 \over 5}$ $m \ne - {1 \over 5}$ và $m \ne - 3$ $m \ne - 3$ nghiệm của phương trình đã cho là $x = {{3m + 2} \over {5m + 1}}$ $x = {{3m + 2} \over {5m + 1}}$

c) Điều kiện của phương trình là $x \ne - 3$ $x \ne - 3$. Khi đó ta có

${{8mx} \over {x + 3}} = (4m + 1)x + 1 \Leftrightarrow 8mx = {\rm{[}}(4m + 1)x + 1](x + 3)$ ${{8mx} \over {x + 3}} = (4m + 1)x + 1 \Leftrightarrow 8mx = {\rm{[}}(4m + 1)x + 1](x + 3)$

$\Leftrightarrow (4m + 1){x^2} + 4(m + 1)x + 3 = 0.(1) (1)$ $\Leftrightarrow (4m + 1){x^2} + 4(m + 1)x + 3 = 0.(1) (1)$

Với $m = - {1 \over 4}$ $m = - {1 \over 4}$ phương trình (1) trở thành

$3x + 3 = 0 \Leftrightarrow x = - 1$ $3x + 3 = 0 \Leftrightarrow x = - 1$

Với $m \ne - {1 \over 4}$ $m \ne - {1 \over 4}$ phương trình (1) là một phương trình bậc hai có

$\Delta$ $\Delta ' = {(2m - 1)^2} \ge 0$

Lúc đó phương trình (1) có hai nghiệm

${x_1} = - {3 \over {4m + 1}},{x_2} = - 1$ ${x_1} = - {3 \over {4m + 1}},{x_2} = - 1$

Ta có $- {3 \over {4m + 1}} \ne - 3 \Leftrightarrow 4m + 1 \ne 1 \Leftrightarrow m \ne 0$ $- {3 \over {4m + 1}} \ne - 3 \Leftrightarrow 4m + 1 \ne 1 \Leftrightarrow m \ne 0$

Kết luận

Với m = 0 hoặc $m = - {1 \over 4}$ $m = - {1 \over 4}$ phương trình đã cho có một nghiệm x = -1.

Với $m \ne 0$ $m \ne 0$ và $m \ne - {1 \over 4}$ $m \ne - {1 \over 4}$ phương trình đã cho có hai nghiệm

x = -1 và $x = - {3 \over {4m + 1}}$ $x = - {3 \over {4m + 1}}$

d) Điều kiện của phương trình là $x \ne 2$ $x \ne 2$. Khi đó ta có

${{(2 - m)x} \over {x - 2}} = (m - 1)x - 1 \Leftrightarrow (2 - m)x = (x - 2){\rm{[}}(m - 1)x - 1]$ ${{(2 - m)x} \over {x - 2}} = (m - 1)x - 1 \Leftrightarrow (2 - m)x = (x - 2){\rm{[}}(m - 1)x - 1]$

$\Leftrightarrow (m - 1){x^2} - (m + 1)x + 2 = 0(2)$ $\Leftrightarrow (m - 1){x^2} - (m + 1)x + 2 = 0(2)$

Với m = 1 phương trình (2) có dạng

$- 2x + 2 = 0 \Leftrightarrow x = 1$ $- 2x + 2 = 0 \Leftrightarrow x = 1$

Với $m \ne 1$ $m \ne 1$ thì phương trình (2) là một phương trình bậc hai có :

$\Delta = {(m - 3)^2} \ge 0$ $\Delta = {(m - 3)^2} \ge 0$

Lúc đó phương trình (2) có hai nghiệm

${x_1} = 1,{x_2} = {2 \over {m - 1}}$ ${x_1} = 1,{x_2} = {2 \over {m - 1}}$

Ta có: ${2 \over {m - 1}} \ne 2 \Leftrightarrow m - 1 \ne 1 \Leftrightarrow m \ne 2$ ${2 \over {m - 1}} \ne 2 \Leftrightarrow m - 1 \ne 1 \Leftrightarrow m \ne 2$

Kết luận:

Với m = 1 và m = 2 phương trình đã cho có một nghiệm là x = 1.

Với m≠1 và m≠2 phương trình đã cho có hai nghiệm

x = 1 và $x=\frac{2}{m-1}$ $x=\frac{2}{m-1}$

Bài 22 trang 77 Sách bài tập (SBT) Toán Đại số 10

Cho phương trình

$3{x^2} + 2(3m - 1)x + 3{m^2} - m + 1 = 0$ $3{x^2} + 2(3m - 1)x + 3{m^2} - m + 1 = 0$

a) Với giá trị nào của m thì phương trình vô nghiệm?

b) Giải phương trình khi m = -1.

Gợi ý làm bài

a) Phương trình vô nghiệm khi $\Delta$ $\Delta ' < 0$

Xét $\Delta$ $\Delta ' = {(3m - 1)^2} - 3(3{m^2} - m + 1) = - 3m - 2$

$\Delta$ $\Delta ' < 0 \Leftrightarrow - 3m - 2 < 0$

$\Leftrightarrow m > - {2 \over 3}$ $\Leftrightarrow m > - {2 \over 3}$

b) Khi m = -1 phương trình đã cho trở thành $3{x^2} - 8x + 5 = 0$ $3{x^2} - 8x + 5 = 0$ và có hai nghiệm ${x_1} = 1;{x_2} = {5 \over 3}$ ${x_1} = 1;{x_2} = {5 \over 3}$

Bài 23 trang 77 Sách bài tập (SBT) Toán Đại số 10

Cho phương trình

$(m + 1){x^2} + (3m - 1)x + 2m - 2 = 0$ $(m + 1){x^2} + (3m - 1)x + 2m - 2 = 0$

Xác định m để phương trình có hai nghiệm $x{}_1,{x_2}$ $x{}_1,{x_2}$ mà $x{}_1 + {x_2} = 3$ $x{}_1 + {x_2} = 3$

Tính các nghiệm trong trường hợp đó.

Gợi ý làm bài

Với m≠−1 ta có: $\Delta = {(m - 3)^2} \ge 0$ $\Delta = {(m - 3)^2} \ge 0$, do đó phương trình luôn luôn có hai nghiệm ${x_1},{x_2}$ ${x_1},{x_2}$

Xét ${x_1} + {x_2} = 3 \Leftrightarrow {{1 - 3m} \over {m + 1}} = 3 \Leftrightarrow m = - {1 \over 3}$ ${x_1} + {x_2} = 3 \Leftrightarrow {{1 - 3m} \over {m + 1}} = 3 \Leftrightarrow m = - {1 \over 3}$

Lúc đó phương trình đã cho có hai nghiệm x = -1 và x = 4.

Bài 24 trang 77 Sách bài tập (SBT) Toán Đại số 10

Giải các phương trình

a) $\sqrt {5x + 3} = 3x - 7$ $\sqrt {5x + 3} = 3x - 7$

b) $\sqrt {3{x^2} - 2x - 1} = 3x + 1$ $\sqrt {3{x^2} - 2x - 1} = 3x + 1$

c) ${{\sqrt {4{x^2} + 7x - 2} } \over {x + 2}} = \sqrt 2$ ${{\sqrt {4{x^2} + 7x - 2} } \over {x + 2}} = \sqrt 2$

d) $\sqrt {2{x^2} + 3x - 4} = \sqrt {7x + 2}$ $\sqrt {2{x^2} + 3x - 4} = \sqrt {7x + 2}$

Gợi ý làm bài

a) Điều kiện của phương trình là $x \ge - {3 \over 5}$ $x \ge - {3 \over 5}$. Ta có

$\sqrt {5x + 3} = 3x - 7 = > 5x + 3 = {(3x - 7)^2}$ $\sqrt {5x + 3} = 3x - 7 = > 5x + 3 = {(3x - 7)^2}$

$\Leftrightarrow 9{x^2} - 47x + 46 = 0$ $\Leftrightarrow 9{x^2} - 47x + 46 = 0$

Phương trình cuối có hai nghiệm ${x_1} = {{47 + \sqrt {553} } \over {18}},{x_2} = {{47 - \sqrt {553} } \over {18}}$ ${x_1} = {{47 + \sqrt {553} } \over {18}},{x_2} = {{47 - \sqrt {553} } \over {18}}$

Cả hai giá trị này đều thỏa mãn điều kiện của phương trình, tuy nhiên khi thay vào phương trình đã cho thì giá trị ${x_2}$ ${x_2}$ bị loại.

Đáp số: ${x_1} = {{47 + \sqrt {553} } \over {18}}$ ${x_1} = {{47 + \sqrt {553} } \over {18}}$

b) Điều kiện của phương trình là $3{x^2} - 2x - 1 \ge 0$ $3{x^2} - 2x - 1 \ge 0$. Ta có:

$\sqrt {3{x^2} - 2x - 1} = 3x + 1 = > 3{x^2} - 2x - 1 = {(3x + 1)^2}$ $\sqrt {3{x^2} - 2x - 1} = 3x + 1 = > 3{x^2} - 2x - 1 = {(3x + 1)^2}$

$\Leftrightarrow 6{x^2} + 8x + 2 = 0$ $\Leftrightarrow 6{x^2} + 8x + 2 = 0$

Phương trình cuối có hai nghiệm ${x_1} = - {1 \over 3},{x_2} = - 1$ ${x_1} = - {1 \over 3},{x_2} = - 1$

Cả hai giá trị này đều thỏa mãn điều kiện của phương trình, nhưng thử vào phương trình đã cho thì giá trị ${x_2} = - 1$ ${x_2} = - 1$ bị loại.

Đáp số: $x = - {1 \over 3}$ $x = - {1 \over 3}$

c) Điều kiện của phương trình là $4{x^2} + 7x - 2 \ge 0$ $4{x^2} + 7x - 2 \ge 0$ và $x \ne - 2$ $x \ne - 2$. Ta có:

${{\sqrt {4{x^2} + 7x - 2} } \over {x + 2}} = \sqrt 2 = > 4{x^2} + 7x - 2 = 2{(x + 2)^2}$ ${{\sqrt {4{x^2} + 7x - 2} } \over {x + 2}} = \sqrt 2 = > 4{x^2} + 7x - 2 = 2{(x + 2)^2}$

$\Leftrightarrow 2{x^2} - x - 10 = 0$ $\Leftrightarrow 2{x^2} - x - 10 = 0$

Phương trình cuối có hai nghiệm là ${x_1} = {5 \over 2},{x_2} = - 2$ ${x_1} = {5 \over 2},{x_2} = - 2$

Chỉ có giá trị ${x_1} = {5 \over 2},{x_2} = - 2$ ${x_1} = {5 \over 2},{x_2} = - 2$

Chỉ có giá trị ${x_1} = {5 \over 2}$ ${x_1} = {5 \over 2}$ thỏa mãn điều kiện và nghiệm đúng phương trình đã cho.

Đáp số: $x = {5 \over 2}$ $x = {5 \over 2}$

d) Điều kiện của phương trình là $2{x^2} + 3x - 4 \ge 0$ $2{x^2} + 3x - 4 \ge 0$ và $7x + 2 \ge 0$ $7x + 2 \ge 0$. Ta có:

$\sqrt {2{x^2} + 3x - 4} = \sqrt {7x + 2} = > 2{x^2} + 3x - 4 = 7x + 2 \Leftrightarrow 2{x^2} - 4x - 6 = 0$ $\sqrt {2{x^2} + 3x - 4} = \sqrt {7x + 2} = > 2{x^2} + 3x - 4 = 7x + 2 \Leftrightarrow 2{x^2} - 4x - 6 = 0$

Phương trình cuối có hai nghiệm ${x_1} = 3,{x_2} = - 1$ ${x_1} = 3,{x_2} = - 1$, nhưng giá trị ${x_2} = - 1$ ${x_2} = - 1$ không thỏa mãn điều kiện của phương tình nên bị loại, giá trị ${x_1} = 3$ ${x_1} = 3$ nghiệm đúng phương trình đã cho.

Vậy nghiệm của phương trình đa cho là x = 3.

Bài 25 trang 77 Sách bài tập (SBT) Toán Đại số 10

Giải và biện luận các phương trình sau theo tham số m.

a) $|2x - 5m| = 2x - 3m$

b) $|3x + 4m| = |4x - 7m|$

c) $(m + 1){x^2} + (2m - 3)x + m + 2 = 0$ $(m + 1){x^2} + (2m - 3)x + m + 2 = 0$

d) ${{{x^2} - (m + 1)x - {{21} \over 4}} \over {x - 3}} = 2x + m$ ${{{x^2} - (m + 1)x - {{21} \over 4}} \over {x - 3}} = 2x + m$

Gợi ý làm bài

a) Với $x \ge {{5m} \over 2}$ $x \ge {{5m} \over 2}$phương trình đã cho trở thành

$2x - 5m = 2x - 3m \Leftrightarrow 2m = 0 \Leftrightarrow m = 0$ $2x - 5m = 2x - 3m \Leftrightarrow 2m = 0 \Leftrightarrow m = 0$

Vậy với m = 0 thì mọi $x \ge 0$ $x \ge 0$ đều là nghiệm của phương trình.

Với $x < {{5m} \over 2}$ $x < {{5m} \over 2}$phương trình đã cho trở thành

$- 2x + 5m = 2x - 3m$

$\Leftrightarrow 4x = 8m \Leftrightarrow x = 2m$ $\Leftrightarrow 4x = 8m \Leftrightarrow x = 2m$

Vì $x < {{5m} \over 2}$ $x < {{5m} \over 2}$ nên $2m < {{5m} \over 2} \Leftrightarrow m > 0$ $2m < {{5m} \over 2} \Leftrightarrow m > 0$

Kết luận:

Với m > 0 phương trình có nghiệm là x = 2m.

Với m = 0 phương trình có nghiệm là mọi số thực không âm.

Với m < 0 phương trình vô nghiệm.

b) Ta có:

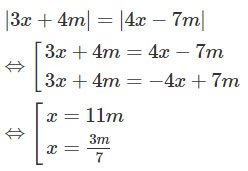
Giải bài tập Toán 10 SBT ôn tập chương 3

Vậy phương trình đã cho có hai nghiệm $x = 11m$ và $x = {{3m} \over 7}$ $x = {{3m} \over 7}$ với mọi giá trị của m.

c) Với m = -1 phương trình đã cho trở thành

$- 5x + 1 = 0 \Leftrightarrow x = {1 \over 5}$ $- 5x + 1 = 0 \Leftrightarrow x = {1 \over 5}$

Với $m \ne - 1$ $m \ne - 1$ phương trình đã cho là một phương trình bậc hai, có biệt thức $\Delta = - 24m + 1.$ $\Delta = - 24m + 1.$

Nếu $m \le {1 \over {24}}$ $m \le {1 \over {24}}$ thì $\Delta \ge 0$ $\Delta \ge 0$ phương trình có hai nghiệm

${x_{1,2}} = {{2m - 3 \pm \sqrt {1 - 24m} } \over {2(m + 1)}}$ ${x_{1,2}} = {{2m - 3 \pm \sqrt {1 - 24m} } \over {2(m + 1)}}$

Kết luận:

Với $x > {1 \over {24}}$ $x > {1 \over {24}}$ phương trình vô nghiệm.

Với $x \le {1 \over {24}}$ $x \le {1 \over {24}}$ và $m \ne - 1$ $m \ne - 1$ phương trình có hai nghiệm.

${x_{1,2}} = {{2m - 3 \pm \sqrt {1 - 24m} } \over {2(m + 1)}}$ ${x_{1,2}} = {{2m - 3 \pm \sqrt {1 - 24m} } \over {2(m + 1)}}$

Với m = -1 phương trình có nghiệm là $x = {1 \over 5}$ $x = {1 \over 5}$

d) Điều kiện của phương trình là: $x \ne 3$ $x \ne 3$ Ta có:

${{{x^2} - (m + 1)x - {{21} \over 4}} \over {x - 3}} = 2x + m = > {x^2} - (m + 1)x - {{21} \over 4} = (x - 3)(2x + m)$ ${{{x^2} - (m + 1)x - {{21} \over 4}} \over {x - 3}} = 2x + m = > {x^2} - (m + 1)x - {{21} \over 4} = (x - 3)(2x + m)$

$\Leftrightarrow {x^2} + (2m - 5)x + {{21} \over 4} - 3m = 0$ $\Leftrightarrow {x^2} + (2m - 5)x + {{21} \over 4} - 3m = 0$

Phương trình cuối luôn có nghiệm ${x_1} = {3 \over 2},{x_2} = {{7 - 4m} \over 2}$ ${x_1} = {3 \over 2},{x_2} = {{7 - 4m} \over 2}$

Ta có: ${{7 - 4m} \over 2} \ne 3 \Leftrightarrow m \ne {1 \over 4}$ ${{7 - 4m} \over 2} \ne 3 \Leftrightarrow m \ne {1 \over 4}$

Kết luận

Với $m \ne {1 \over 4}$ $m \ne {1 \over 4}$ phương trình đã cho có hai nghiệm và $x = {3 \over 2}$ $x = {3 \over 2}$ và $x = {{7 - 4m} \over 2}$ $x = {{7 - 4m} \over 2}$

Với $m = {1 \over 4}$ $m = {1 \over 4}$ phương trình có một nghiệm $x = {3 \over 2}$ $x = {3 \over 2}$

Bài 26 trang 78 Sách bài tập (SBT) Toán Đại số 10

Giải phương trình

Giải bài tập Toán 10 SBT ôn tập chương 3

(2) $\Leftrightarrow u({u^2} + u - 2) = 0$ $\Leftrightarrow u({u^2} + u - 2) = 0$

Phương trình cuối có 3 nghiệm ${u_1} = 0,{u_2} = 1,{u_3} = 2$ ${u_1} = 0,{u_2} = 1,{u_3} = 2$

+ Với u = 0 ta có v = 1 => $x = - {1 \over 2}$ $x = - {1 \over 2}$

+ Với u =1 ta có v = 0 => $x = {1 \over 2}$ $x = {1 \over 2}$

+ Với u = -2 ta có v = 3 => $x = - {{17} \over 2}$ $x = - {{17} \over 2}$

Vậy phương trình đã cho có ba nghiệm

$x = - {1 \over 2}$ $x = - {1 \over 2}$, $x = {1 \over 2}$ $x = {1 \over 2}$ và $x = - {{17} \over 2}$ $x = - {{17} \over 2}$

Bài 27 trang 78 Sách bài tập (SBT) Toán Đại số 10

Giải các hệ phương trình

a) $\left\{ \matrix{- 7x + 3y = - 5 \hfill \cr 5x - 2y = 4; \hfill \cr} \right.$ $\left\{ \matrix{- 7x + 3y = - 5 \hfill \cr 5x - 2y = 4; \hfill \cr} \right.$

b) $\left\{ \matrix{4x - 2y = 6 \hfill \cr - 2x + y = - 3 \hfill \cr} \right.$ $\left\{ \matrix{4x - 2y = 6 \hfill \cr - 2x + y = - 3 \hfill \cr} \right.$

c) $\left\{ \matrix{- 0,5x + 0,4y = 0,7 \hfill \cr 0,3x - 0,2y = 0,4; \hfill \cr} \right.$ $\left\{ \matrix{- 0,5x + 0,4y = 0,7 \hfill \cr 0,3x - 0,2y = 0,4; \hfill \cr} \right.$

d) $\left\{ \matrix{{3 \over 5}x - {4 \over 3}y = {2 \over 5} \hfill \cr - {2 \over 3}x - {5 \over 9}y = {4 \over 3}; \hfill \cr} \right.$ $\left\{ \matrix{{3 \over 5}x - {4 \over 3}y = {2 \over 5} \hfill \cr - {2 \over 3}x - {5 \over 9}y = {4 \over 3}; \hfill \cr} \right.$

Gợi ý làm bài

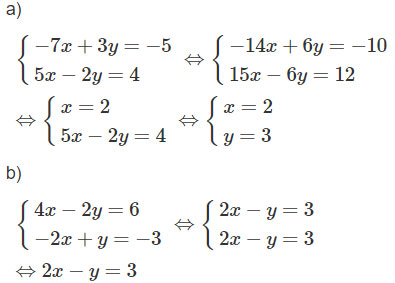
Giải bài tập Toán 10 SBT ôn tập chương 3

Vậy hệ phương trình có vô số nghiệm $(x;y) = (a;2a - 3)$, a tùy ý.

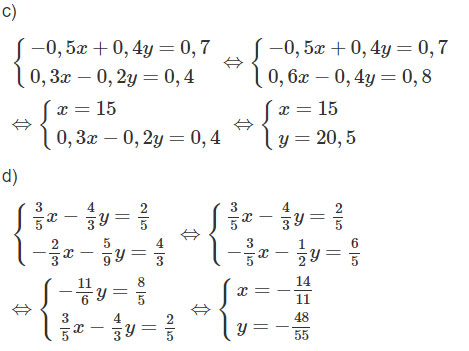
Giải bài tập Toán 10 SBT ôn tập chương 3

Bài 28 trang 78 Sách bài tập (SBT) Toán Đại số 10

Giải các hệ phương trình

a) $\left\{ \matrix{x + 2y - 3z = 2 \hfill \cr 2x + 7y + z = 5 \hfill \cr - 3x + 3y - 2z = - 7; \hfill \cr} \right.$ $\left\{ \matrix{x + 2y - 3z = 2 \hfill \cr 2x + 7y + z = 5 \hfill \cr - 3x + 3y - 2z = - 7; \hfill \cr} \right.$

b) $\left\{ \matrix{- x - 3y + 4z = 3 \hfill \cr 3x + 4y - 2z = 5 \hfill \cr 2x + y + 2z = 4; \hfill \cr} \right.$ $\left\{ \matrix{- x - 3y + 4z = 3 \hfill \cr 3x + 4y - 2z = 5 \hfill \cr 2x + y + 2z = 4; \hfill \cr} \right.$

Gợi ý làm bài

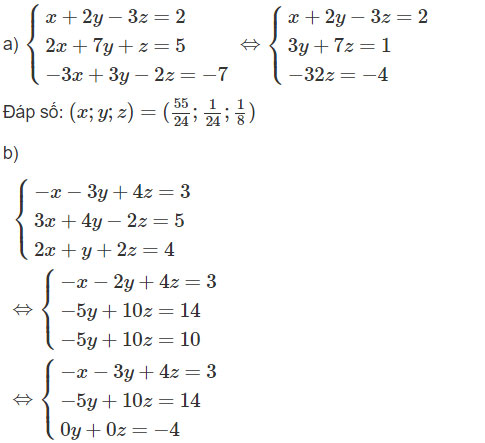
Giải bài tập Toán 10 SBT ôn tập chương 3

Phương trình cuối vô nghiệm, suy ra hệ phương trình đã cho vô nghiệm.

Bài 29 trang 78 Sách bài tập (SBT) Toán Đại số 10

Tìm các giá trị của a và b để các hệ phương trình sau có vô số nghiệm

a) $\left\{ \matrix{3x + ay = 5 \hfill \cr 2x + y = b; \hfill \cr} \right.$ $\left\{ \matrix{3x + ay = 5 \hfill \cr 2x + y = b; \hfill \cr} \right.$

b) $\left\{ \matrix{ax + 2y = a \hfill \cr 3x - 4y = b + 1. \hfill \cr} \right.$ $\left\{ \matrix{ax + 2y = a \hfill \cr 3x - 4y = b + 1. \hfill \cr} \right.$

Gợi ý làm bài

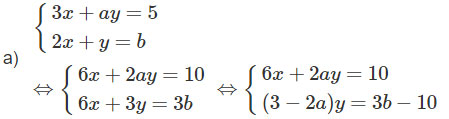
Giải bài tập Toán 10 SBT ôn tập chương 3

Phương trình $(3 - 2a)y = 3b - 10$ vô số nghiệm khi và chỉ khi

$\left\{ \matrix{3 - 2a = 0 \hfill \cr 3b - 10 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = {3 \over 2} \hfill \cr b = {{10} \over 3} \hfill \cr} \right.$ $\left\{ \matrix{3 - 2a = 0 \hfill \cr 3b - 10 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = {3 \over 2} \hfill \cr b = {{10} \over 3} \hfill \cr} \right.$

Vậy hệ phương trình đã cho vô số nghiệm khi $a = {3 \over 2},b = {{10} \over 3}$ $a = {3 \over 2},b = {{10} \over 3}$

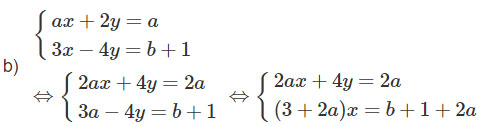
Giải bài tập Toán 10 SBT ôn tập chương 3

Phương trình $(3 + 2a)x = b + 1 + 2a$ vô nghiệm khi và chỉ khi

$\left\{ \matrix{3 + 2a = 0 \hfill \cr b + 1 + 2a = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = - {3 \over 2} \hfill \cr b = 2 \hfill \cr} \right.$ $\left\{ \matrix{3 + 2a = 0 \hfill \cr b + 1 + 2a = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = - {3 \over 2} \hfill \cr b = 2 \hfill \cr} \right.$

Vậy hệ phương trình đã cho vô số nghiệm khi $a = - {3 \over 2},b = 2$ $a = - {3 \over 2},b = 2$

Bài 30 trang 78 Sách bài tập (SBT) Toán Đại số 10

Một gia đình có bốn người lớn và ba trẻ em mua vé xem xiếc hết 370 000 đồng. Một gia đình khác có hai người lớn và hai trẻ em cũng mua vé xem xiếc tại rạp đó hết 200 000 đồng. Hỏi giá vé người lớn và giá vé trẻ em là bao nhiêu.

Gợi ý làm bài

Gọi x (đồng) là giá vé người lớn, y (đồng) là giá vé trẻ em (điều kiện x > 0, y > 0). Ta có hệ phương trình:

$\left\{ \matrix{4x + 3y = 370000 \hfill \cr 2x + 2y = 200000 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{x + y = 100000 \hfill \cr - y = - 30000 \hfill \cr} \right.$ $\left\{ \matrix{4x + 3y = 370000 \hfill \cr 2x + 2y = 200000 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{x + y = 100000 \hfill \cr - y = - 30000 \hfill \cr} \right.$

Suy ra y = 30 000, x = 70 000.

Vậy giá vé người lớn là 70 000 đồng, giá vé trẻ em là 30 000 đồng.

Bài 31 trang 79 Sách bài tập (SBT) Toán Đại số 10

Nếu lấy một số có hai chữ số chia cho tích hai chữ số của nó thì được thương là 2 và dư là 18. Nếu lấy tổng bình phương các chữ số của số đó cộng với 9 thì được số đã cho. Hãy tìm số đó.

Gợi ý làm bài

Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1≤a≤9 và 0≤b≤9. Ta có:

$\left\{ \matrix{10a + b = 2ab + 18 \hfill \cr {a^2} + {b^2} + 9 = 10a + b \hfill \cr} \right.$ $\left\{ \matrix{10a + b = 2ab + 18 \hfill \cr {a^2} + {b^2} + 9 = 10a + b \hfill \cr} \right.$

$=> {a^2} + {b^2} + 9 = 2ab + 18$ $=> {a^2} + {b^2} + 9 = 2ab + 18$

$=> {(a - b)^2} = 9 = > a - b = \pm 3$ $=> {(a - b)^2} = 9 = > a - b = \pm 3$

Trường hợp 1

a - b = 3 => a = b + 3

Thay vào phương trình đầu của hệ phương trình ta được:

$11b + 30 = 2(b + 3)b + 18 = > 2{b^2} - 5b - 12 = 0$ $11b + 30 = 2(b + 3)b + 18 = > 2{b^2} - 5b - 12 = 0$

Phương trình cuối có hai nghiệm: ${b_1} = 4,{b_2} = - {3 \over 2}$ ${b_1} = 4,{b_2} = - {3 \over 2}$

Giá trị ${b_2} = - {3 \over 2}$ ${b_2} = - {3 \over 2}$ không thỏa mãn điều kiện $0 \le b \le 9$ $0 \le b \le 9$ nên nên bị loại.

Vậy b = 4, suy ra a = 7.

Trường hợp 2

a - b = - 3 => a = b - 3

Thay vào phương trình của hệ phương trình ra được

$11b - 30 = 2(b - 3)b + 18 = > 2{b^2} - 17b + 48 = 0$ $11b - 30 = 2(b - 3)b + 18 = > 2{b^2} - 17b + 48 = 0$

Phương trình này vô nghiệm.

Vậy số phải tìm là 74.

Bài 32 trang 79 Sách bài tập (SBT) Toán Đại số 10

Một đoàn xe tải chở 290 tấn xi măng cho một công trình xây đập thủy điện. Đoàn xe có 57 chiếc gồm ba loại, xe chở 3 tấn, xe chở 5 tấn và xe chở 7,5 tấn. Nếu dùng tất cả xe 7,5 tấn chở ba chuyến thì được số xi măng bằng tổng số xi măng do xe 5 tấn chở ba chuyến và xe 3 tấn chở hai chuyến. Hỏi số xe mỗi loại?

Gợi ý làm bài

Gọi x là số xe tải chở 3 tấn, y là số xe chở 5 tấn và z là số xe tải chở 7,5 tấn. Điều kiện x, y, z nguyên dương.

Theo giả thiết của bài toán ta có:

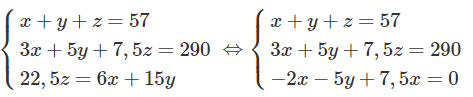
Giải bài tập Toán 10 SBT ôn tập chương 3

Cộng từng vế phương trình thứ hai với phương trình thứ ba ta được hệ phương trình

$\left\{ \matrix{x + y + z = 57 \hfill \cr 3x + 5y + 7,5z = 290 \hfill \cr x + 15z = 290 \hfill \cr} \right.$ $\left\{ \matrix{x + y + z = 57 \hfill \cr 3x + 5y + 7,5z = 290 \hfill \cr x + 15z = 290 \hfill \cr} \right.$

Nhân hai vế của phương trình thứ nhất với -5 rồi cộng từng vế với phương trình thứ hai ta được

$\left\{ \matrix{x + y + z = 57 \hfill \cr - 2x + 2,5y = 5 \hfill \cr x + 15z = 290 \hfill \cr} \right.$ $\left\{ \matrix{x + y + z = 57 \hfill \cr - 2x + 2,5y = 5 \hfill \cr x + 15z = 290 \hfill \cr} \right.$

Từ phương trình cuối suy ra x = 290 – 15z

Thay giá trị tìm được của x vào phương trình thứ hai ta được 32,5z=585 hay z = 18.

Từ đó suy ra x = 20, y = 19. Các giá trị của x, y, z vừa tìm được thỏa mãn điều kiện của bài toán.

Vậy có 20 xe chở 3 tấn, 19 xe chở 5 tấn và 18 xe chở 7,5 tấn.

Bài 33 trang 79 Sách bài tập (SBT) Toán 10

Giải và biện luận theo tham số m hệ phương trình:

$\left\{ \matrix{2x(3m + 1)y = m - 1 \hfill \cr (m + 2)x + (4m + 3)y = m \hfill \cr} \right.$ $\left\{ \matrix{2x(3m + 1)y = m - 1 \hfill \cr (m + 2)x + (4m + 3)y = m \hfill \cr} \right.$

Hướng dẫn: Giải và biện luận theo m có nghĩa là xét xem với giá trị nào của m thì hệ phương trình vô nghiệm, với giá trị nào của m thì hệ phương trình có 1 nghiệm, giá trị nghiệm là bao nhiêu, với giá trị nào của m thì hệ phương trình có vô số nghiệm.

Để Giải và biện luận hệ phương trình trên ta dùng phương pháp cộng đại số để khử một ẩn.

Gợi ý làm bài

Nhân phương trình thứ nhất của hệ với m + 2, nhân phương trình thứ hai với 2 ta được hệ phương trình

$\left\{ \matrix{2(m + 2)x + (3m + 1)(m + 2)y = (m - 1)(m + 2) \hfill \cr 2(m + 2)x + 2(4m + 3)y = 2m \hfill \cr} \right.$ $\left\{ \matrix{2(m + 2)x + (3m + 1)(m + 2)y = (m - 1)(m + 2) \hfill \cr 2(m + 2)x + 2(4m + 3)y = 2m \hfill \cr} \right.$

Trừ hai phương trình vế theo vế ta được phương trình:

$(3{m^2} - m - 4)y = (m + 1)(m - 2) (1)$ $(3{m^2} - m - 4)y = (m + 1)(m - 2) (1)$

+Với m = -1 phương trình (1) có dạng:

0y = 0

Phương trình này nhận mọi giá trị thức của y làm nghiệm. Lúc đó thay m = -1 vào hệ phương trình đã cho, hai phương trình trở thành một phương trình.

$x - y = - 1 = > y = x + 1$, x tùy ý.

+Với $m = {4 \over 3}$ $m = {4 \over 3}$ phương trình (1) có dạng.

$0y = - {{14} \over 9}$ $0y = - {{14} \over 9}$

Phương trình này vô nghiệm, do đó hệ phương trình đã cho vô nghiệm.

+Với $m \ne - 1$ $m \ne - 1$ và $m \ne {4 \over 3}$ $m \ne {4 \over 3}$, phương trình (1) có nghiệm duy nhất

$y = {{m - 2} \over {3m - 4}}$ $y = {{m - 2} \over {3m - 4}}$

Thay vào một trong hai phương trình của hệ đã cho ta suy ra

$x = {{ - m + 3} \over {3m - 4}}$ $x = {{ - m + 3} \over {3m - 4}}$

Kết luận

$m = {4 \over 3}$ $m = {4 \over 3}$: Hệ phương trình đã cho vô nghiệm.

$m = - 1$: Hệ phương trình đã cho có vô số nghiệm

$x = a,y = a + 1$, a là số thực tùy ý.

$m \ne - 1$ $m \ne - 1$ và $m \ne {4 \over 3}$ $m \ne {4 \over 3}$: Hệ phương trình đã cho có nghiệm duy nhất:

$m \ne - 1$ $m \ne - 1$ và $(x;y) = ({{3 - m} \over {3m - 4}};{{m - 2} \over {3m - 4}})$ $(x;y) = ({{3 - m} \over {3m - 4}};{{m - 2} \over {3m - 4}})$

-----------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.